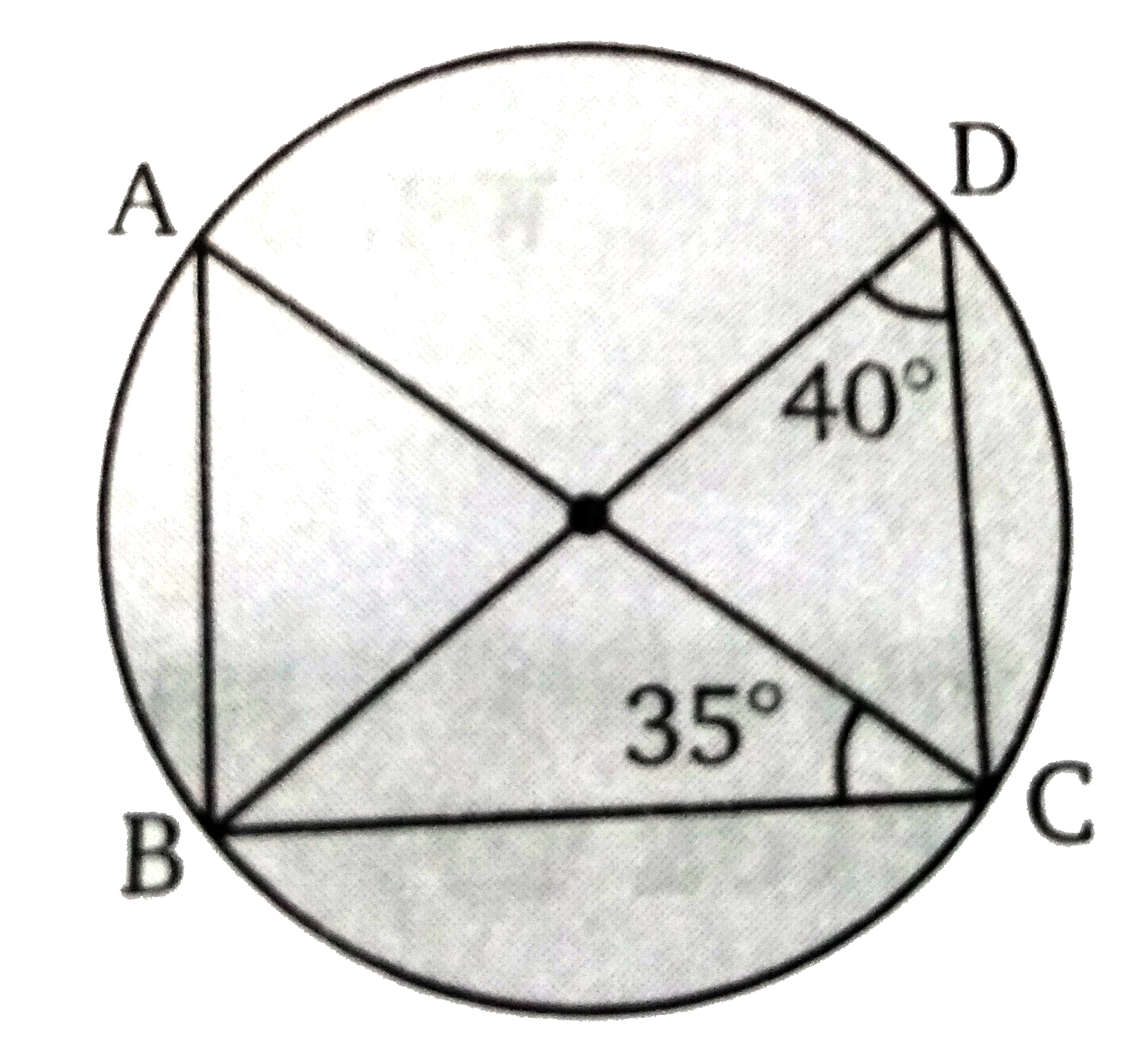
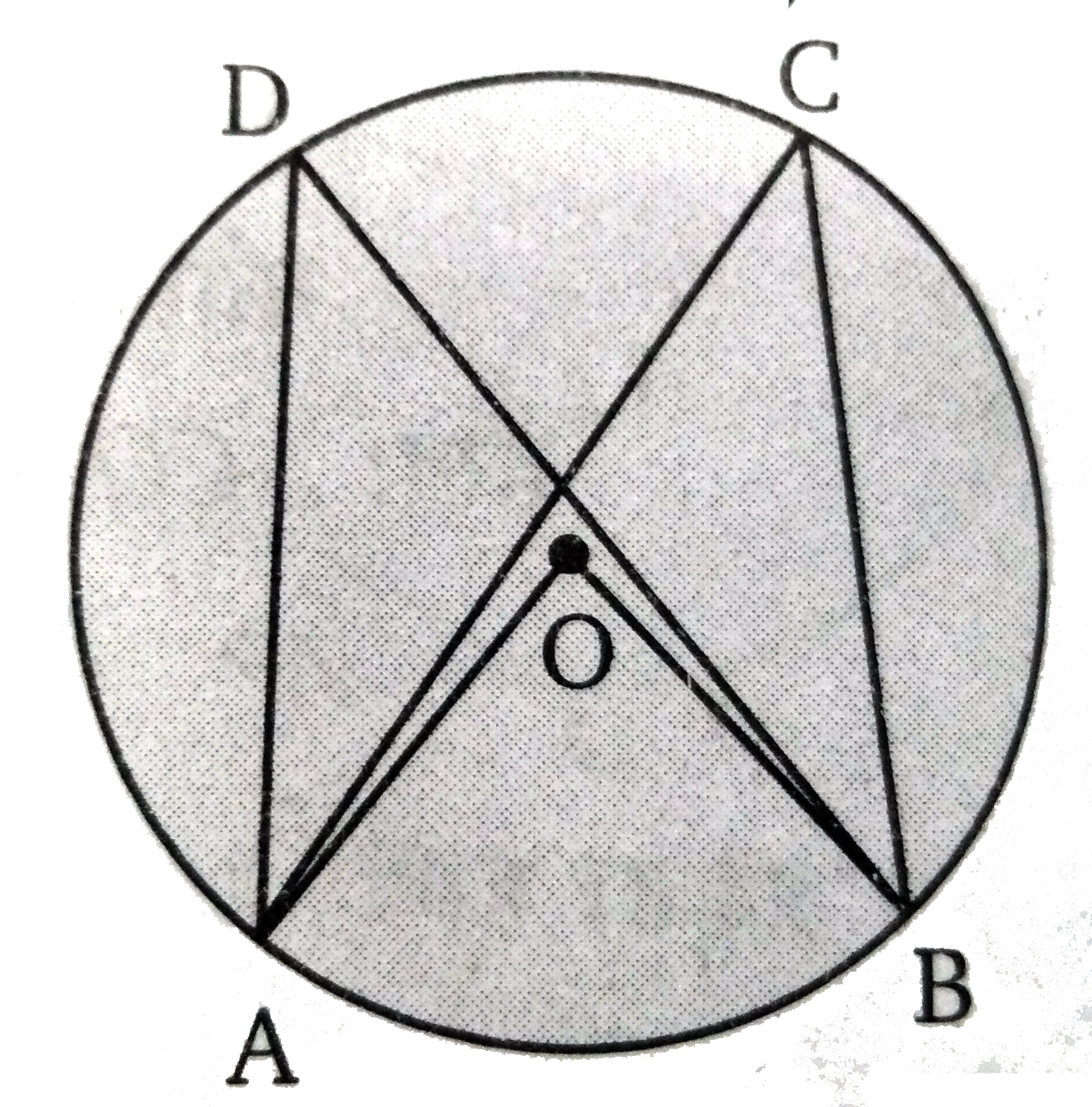
O is centre of the cricle. If ∠AOD=40∘and∠ACB=35∘, then the find the value of ∠BCOand∠BOD.Solution in Bengali
The central angle produced by the are ⌢AB=∠AOBand the angle in circle =∠ACB=35∘ (Given)
∴ by theroem -34 ∠AOB=2∠ACB=2×35∘=70∘
Again, the central angle produced by ⌢AD=∠AOD and angle in cricle = ∠ACDor∠ACO.

∴ by theorem-34 ∠=2∠ACO
or, 40∘=2∠ACO[∴∠AOD=40∘ ( Given)]
or, ∠ACO=40∘2=20∘,
Now, ∠BCO=∠ACB+∠ACO=35∘+20∘=55∘[∴∠ACB=35∘(Given)and∠ACO=20∘]
and ∠BOC=∠AOB+∠AOB=40∘+70∘=110∘[∴∠AOB=40∘(Given)and∠AOB=70∘]
∴∠BCO=55∘and∠BOD=110∘
Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
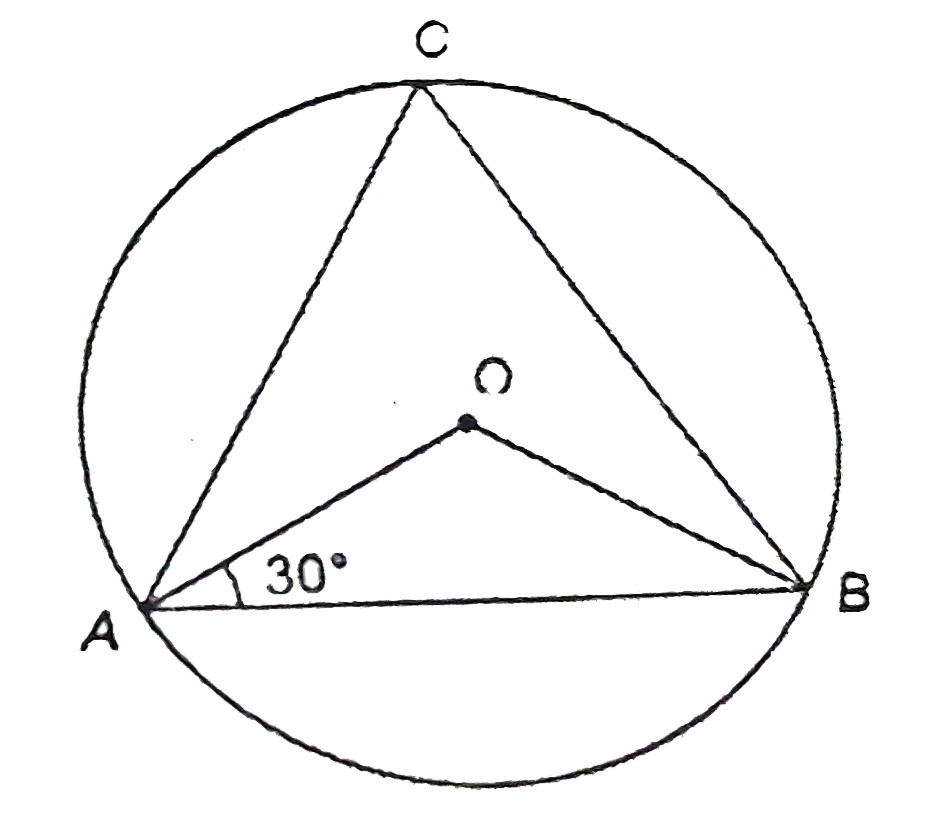
View SolutionIn the adjoining , O is the centre of the circle. ACB is a segment. If ∠OAB=30∘, then find the value of ∠ACB.
View SolutionIn the following figure, O is the centre of the circle. AB is an arc of the circle, such that ∠AOB=80∘.Find ∠ACB.
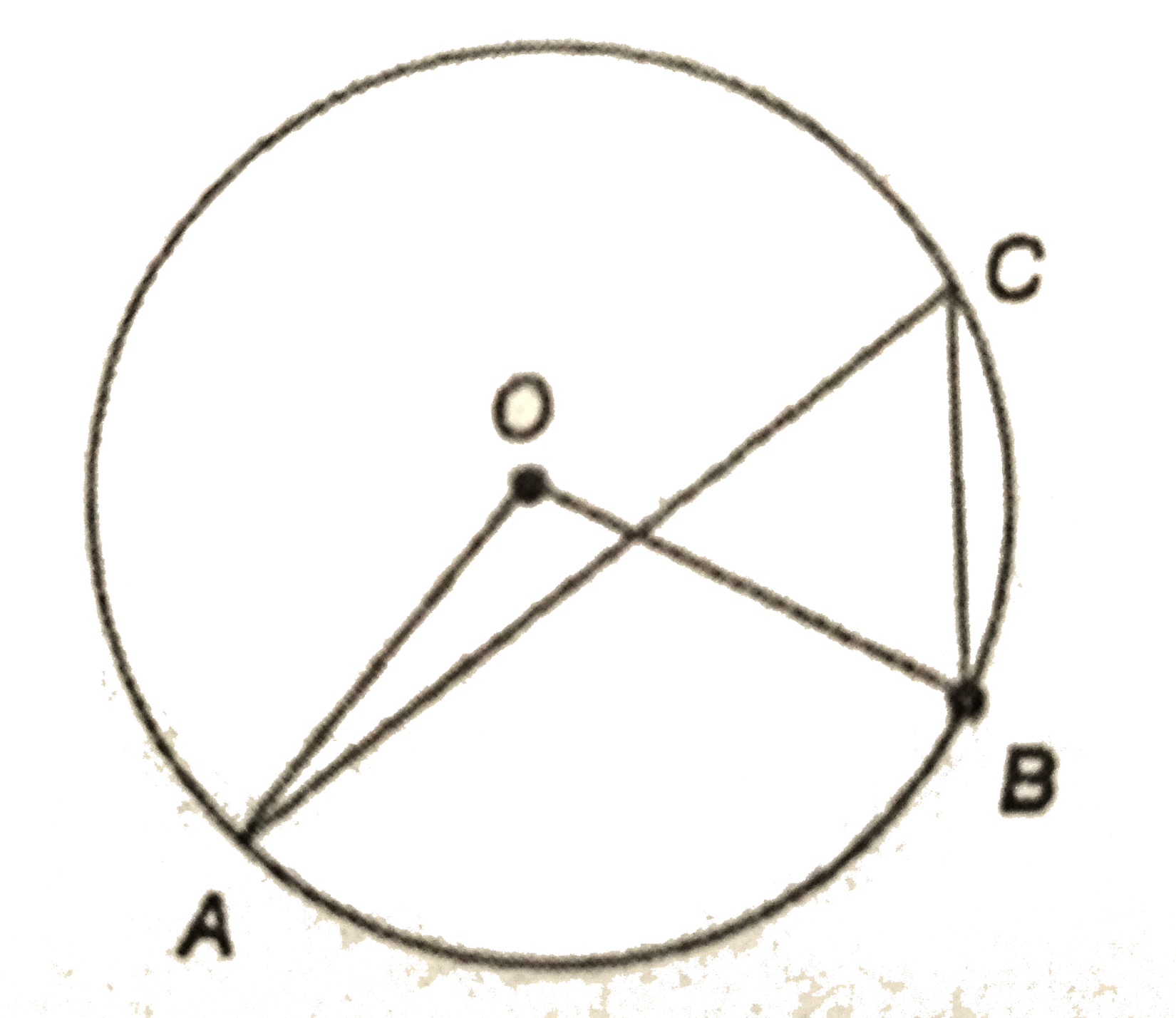
View SolutionIn the following fiure. O is the centr of the circle and AD is the diameter. If ∠ACB=135∘ , then find ∠DOB.

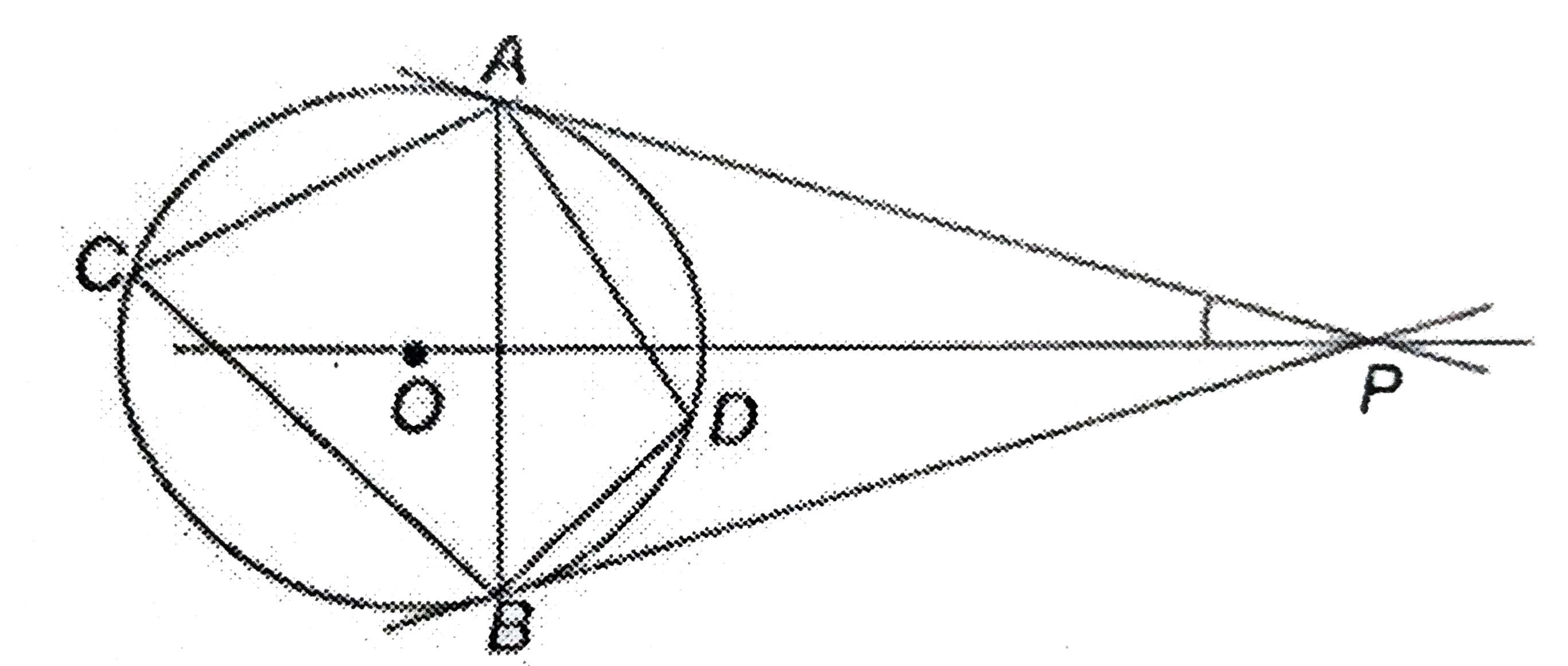
View SolutionIn the diagram , O is the centre of the circle and ∠OPA=30∘, Find ∠ACBand∠ADB respectively.
View SolutionABCD is a rhombus such that ∠ACB=40∘. Find ∠ADB.
View Solutionबिंदु O से जाने वाली तीन संगमि रेखाएं AB ,CD तथा EF इस प्रकार है की किरण OF कोण ∠BOD के समद्विभाजित करती है|यदि ∠BOF=35∘ तो ∠BOC तथा ∠AOD का मान ज्ञात कीजिए|
View SolutionABCD एक समांतर चतुर्भुज है जिसमे ∠A तथा ∠D के समद्विभुज बिंदु O पर प्रतिच्छेद करते है , तो ∠AOD का मान ज्ञात कीजिये ।
View Solutionचित्र में ∠BCA=35∘,∠CDB=40∘ तब ∠ABC का मान ज्ञात कीजिए
View Solutionचित्र में, O वृत्त का केन्द्र है तथा ∠ACB व ∠ADB समान वृत्तखण्ड के कोण हैं तब ∠ADB व ∠ACB में सम्बन्ध ज्ञात कीजिए
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View Solution
