Question

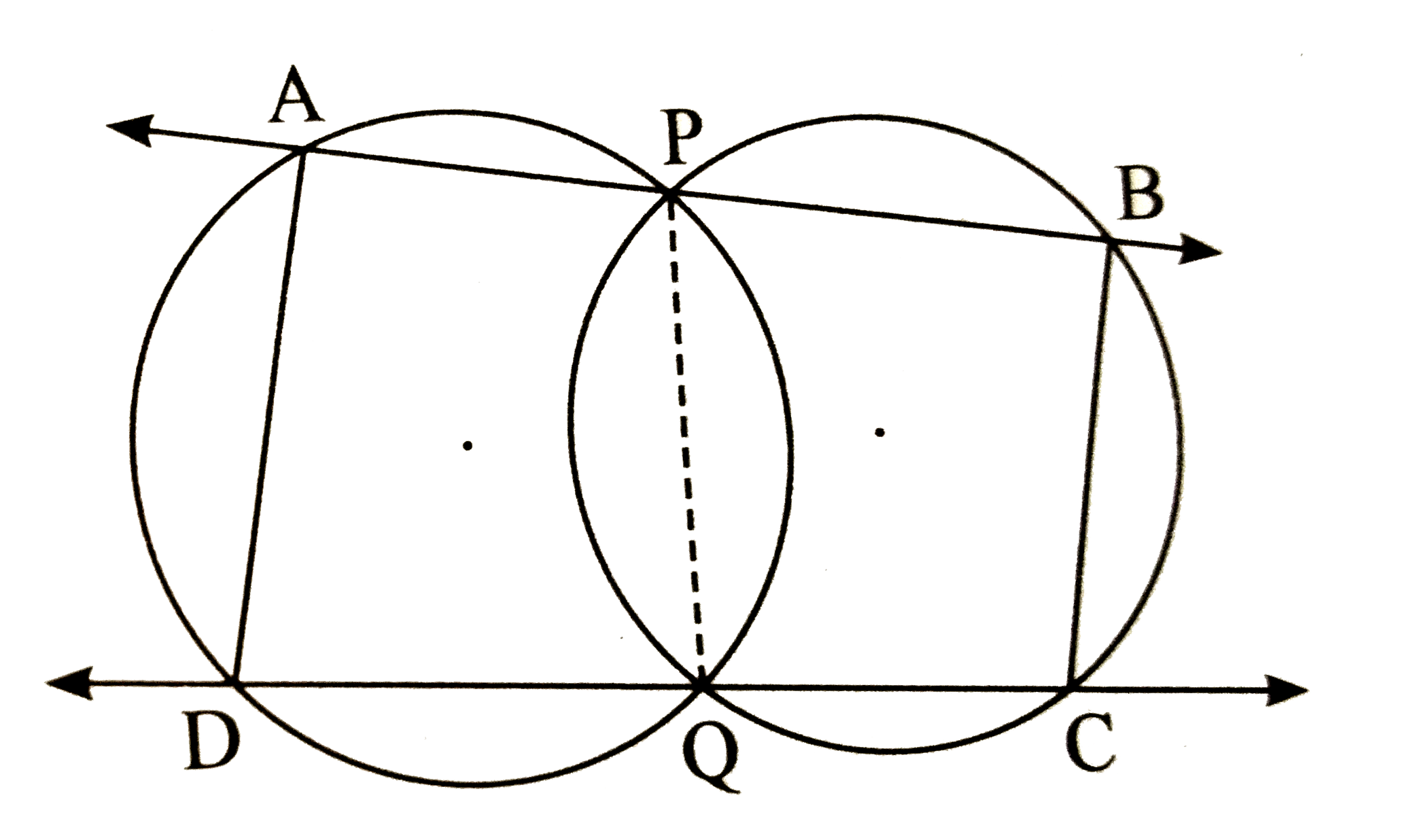
Each of the two equal circles passes through the centre of the other and the two circles intersect each other at the points. A and B.If a straight ine through the point A intersects the two circles at points C and D prove that ${\displaystyle \Delta BCD}$ is an equilateral triangle.

Explanation

Let the two circles centres at P and Q respectively are equal. The two circles ech other at A and B. the staright line CD passes throughh A and intersect the circle with centre P at C and with centre Q at D.
To prove : We have to prove that `DeltaBCD` is equilateral.
Construction : Let us join `P, Q, A, P, B, P, Q, and B, Q`. let PQ intersect AB at S.
Proof : In triangles `Delta APS and Delta BPS, AP= BP [ :. ` radii of same circle]
`AS=BS [ :. S` is the mid- point of AB] and PS is common to both.
`:. Delta APS~= Delta BPS :. angle APS = angle BPS [ :.` smilar angles of congreunt triangles] .....(1)
Now, the circle cenre at P, the angle in circle produced by the are `overset( frown) (AB)= angle ACB` and the central angle `=angle APB`.
`:. angle APB= 2 ACB` [ by theorem-34]
or, `angle APS+ angle BPS= 2 angle ACB`
or, `angle APS+ angle APS= 2 angle ACB`
or, ` 2 angle APS= 2 angle ACB= or, angle APS= angle ACB ......(2)`
Also in the circle with centre at Q, the central angle produced by the arc `overset(frown)(ADB)`= reflex `angle AQB` and angle in circle `= angle APB`.
`:.` by theorem-34 reflex `angle AQB= 2 angle APB`
`or, 360^(@),-angleAQB=2 angle APB`
`or, 360^(@)- angle APB=2 angle APB [ :. angle AQB= angle APB]`
Since `Delta APS~= Delta AQS rArr angle APS = angle AQS`
Similarly, `angle BPS= angle BQS]`

or, `360^(@), 3 angle APB or, angle APB=(360^(@))/(3)=120^(@)`
or `2 angle APS= 120^(@) [ :. angleAPB=2 angle APS]`
or, ` angle APS=(120^(@))/(2)=60^(@)`
`:. angle ACB=60^(@)` [ from (2)]
Similary it can be proved that ` angleBDC=60^(@)`
`:.` the other angle of `Delta ABC` is `60^(@)` .
i.e., in triangle `BCD, angle BCD= angle BDC= angle CBD=60^(@)`
Hence `Delta ABC` is an equilateral triangle.