Question

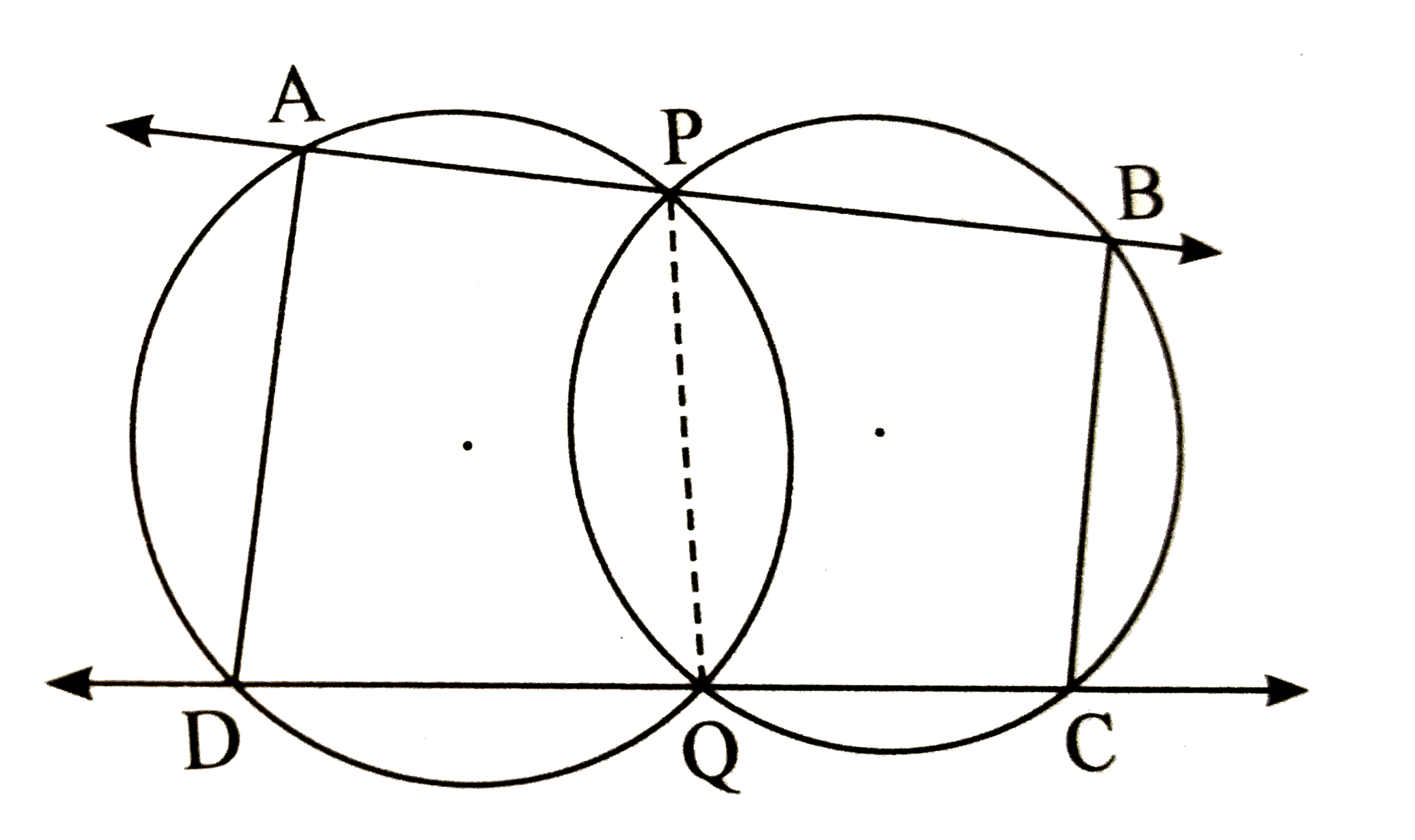
Ankita drew two circles which intersect each other at the points P and Q. Through the point P two straight lines are draw so that they intersect one of the circle at the points. A and B and the ohte circle at the points C and D respectively. Prove that $\angle AQC=\angle BQD$.

Explanation

Two circle with centres at O and O' resepctively intersect each other at the points P and Q. Through the point P two straight lines APC and BPD are drawn which intesect the first circle at A and B the second circle at C and D respectively.
To prove : We have to prove that `angle AQC= angle BQD`
Construction : Let us join `A,Q , B,Q, C,Q and D,Q`
Proof : `angleAPB and angle AQB` are two angles in circle produced by the are `overset(frown)(AB)` in the circle with centre at O.
`:. angle APB= angle AQB......(1)`
Again, `angle CQD and angleCPD` are two angles in circle produced by the are `overset(frown)(CD)` in the circle with centre at ,
`:. angleCQD= angle CPD.......(2)`
But, `angleAPB= angle CPD [ :.` opposite angle]
`:. angle AQB= angle CQD` [ from (1) and (2)]]
Now, `angle AQD+ angle AQB= angle AQD+ angle CQD[ :. angle AQB= angle CQD] or, angle BQD= angle AQC`
`:. angle AQC= angle BQD`