In the isosceles ΔABC,AB=AC. The circumcentre of ΔABC is the centre O lies on the opposite side of BC in which a lies. If ΔBOC=100∘, then find the value of ∠ABC∠ABO. Solution in Bengali
In ΔBOC,OB,OC[∴ radii of same circle]
∴∠OBC=∠OCB
or, ∠OBC+∠OBC=∠OCB+∠OBC
or, 2∠OBC=180∘−∠BOCor,2∠OBC=180∘−100∘
or, 2∠OBC=810∘or,∠OBC=80∘2=40∘

Again, the centralangle produced by the are ⌢BC=∠BOC and the angle in cricle =∠BAC.
By theorem -34, ∠BOC=2∠BAC.
or, ∠BAC=12∠BOC=12×100∘=50∘
Now, angleABC=180∘−(∠ACB+∠BAC)
=180∘−∠ABC−50∘[∴∠ACB=∠ABCand∠BAC=50∘]
=130∘−∠ABC
or, 2∠ABC=130∘,or∠ABC=130∘2=65∘
Then ∠ABO=∠ABC−∠OBC=65∘−40∘=25∘
Hence, ∠ABC=65∘and∠ABO=25∘
Topper's Solved these Questions
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (True or False)
4 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short-Answer Type Questions) MCQs
5 Videos
- THEOREMS RELATED TO ANGLES IN A CIRCLEBOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO ANGLES IN A CIRCLEEXERCISE - EXAMPLES (Short Answer Type Questions)
5 Videos
- THEOREMS RELATED TO CYCLIC QUADRILATERAL BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO CYCLIC QUADRILATERAL EXERCISE - Long -answer type questions (L.A.)
12 Videos
- THEOREMS RELATED TO TANGENT IN A CIRCLE BOOK - CALCUTTA BOOK HOUSECHAPTER - THEOREMS RELATED TO TANGENT IN A CIRCLE EXERCISE - EXERCISE 4.2
23 Videos
Similar Questions
In the adjoining figure AD and BE are perpendicular ot BC and AC respectively of the ΔABC. The four points A,B,D,E are concylic.
View SolutionIn the adjoining figure, O is the centre of the circle AC is a diameter and chord DE is parallel to the diameter AC. If ∠CBD=60∘ , find the value of ∠CDE
View SolutionIn the adjacent figure O is the centre of the circle. If ∠OAB=30∘,∠ABC=120∘,∠BCO=y∘and∠COA=x∘, then the find value sof x and y.
View SolutionIn a cyclic quadrilateral, the ratio of three consecutive angle is 1 : 2 : 3 Find the value of first and third angles.
View SolutionThe distance of the point from the centre of a circle with diameter of 16 cm is 17 cm. Then the length of the tangent from the point to the circle is
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC = BC है । यदि AB2=2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
View SolutionΔABC में, ∠A का समद्विभाजक AD भुजा BC पर लम्ब है। दर्शाइए कि AB = AC है और ΔABC समद्विबाहु है।
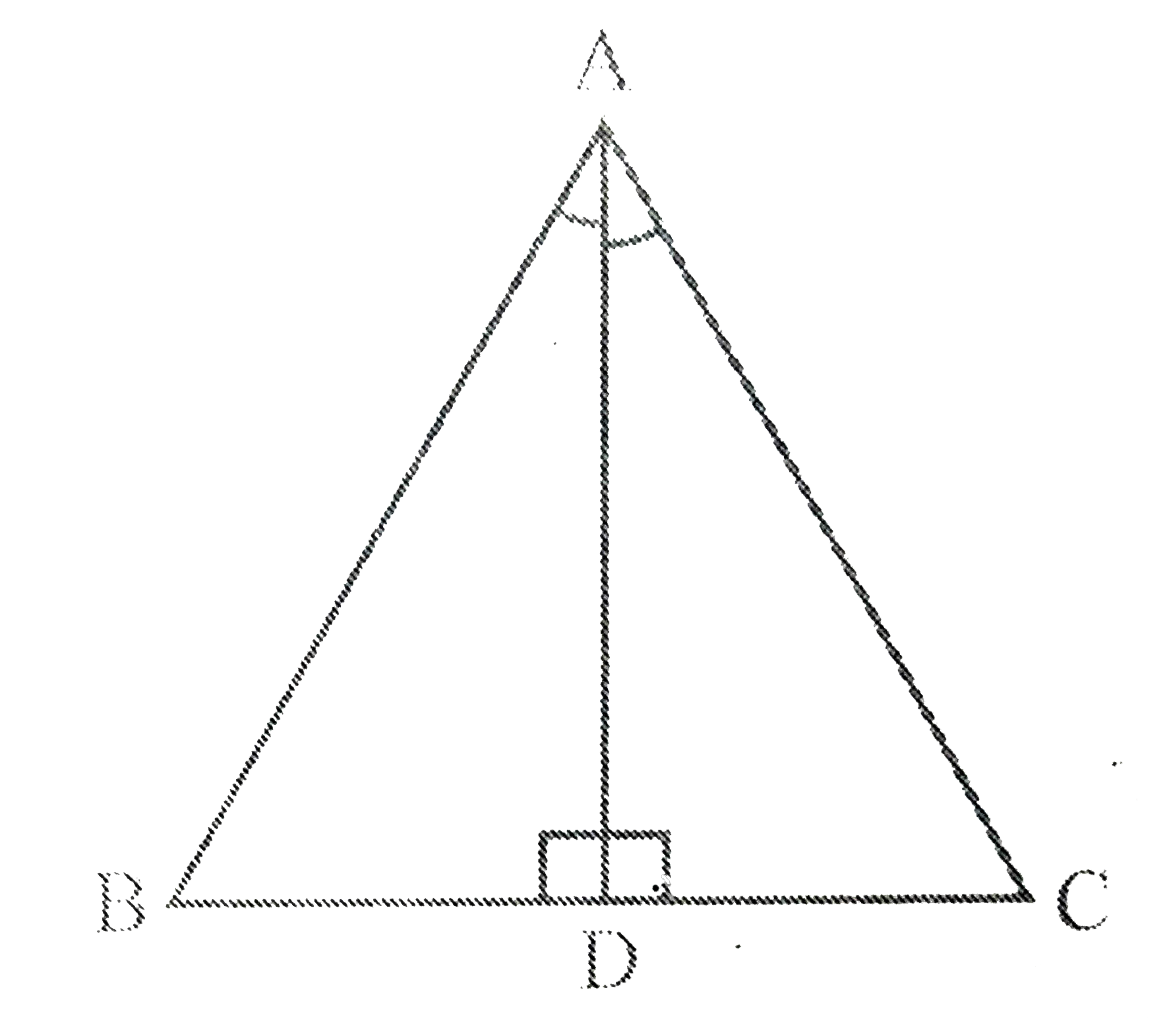
View SolutionΔABC में AD भुजा BC का लम्ब समद्विभाजक है। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
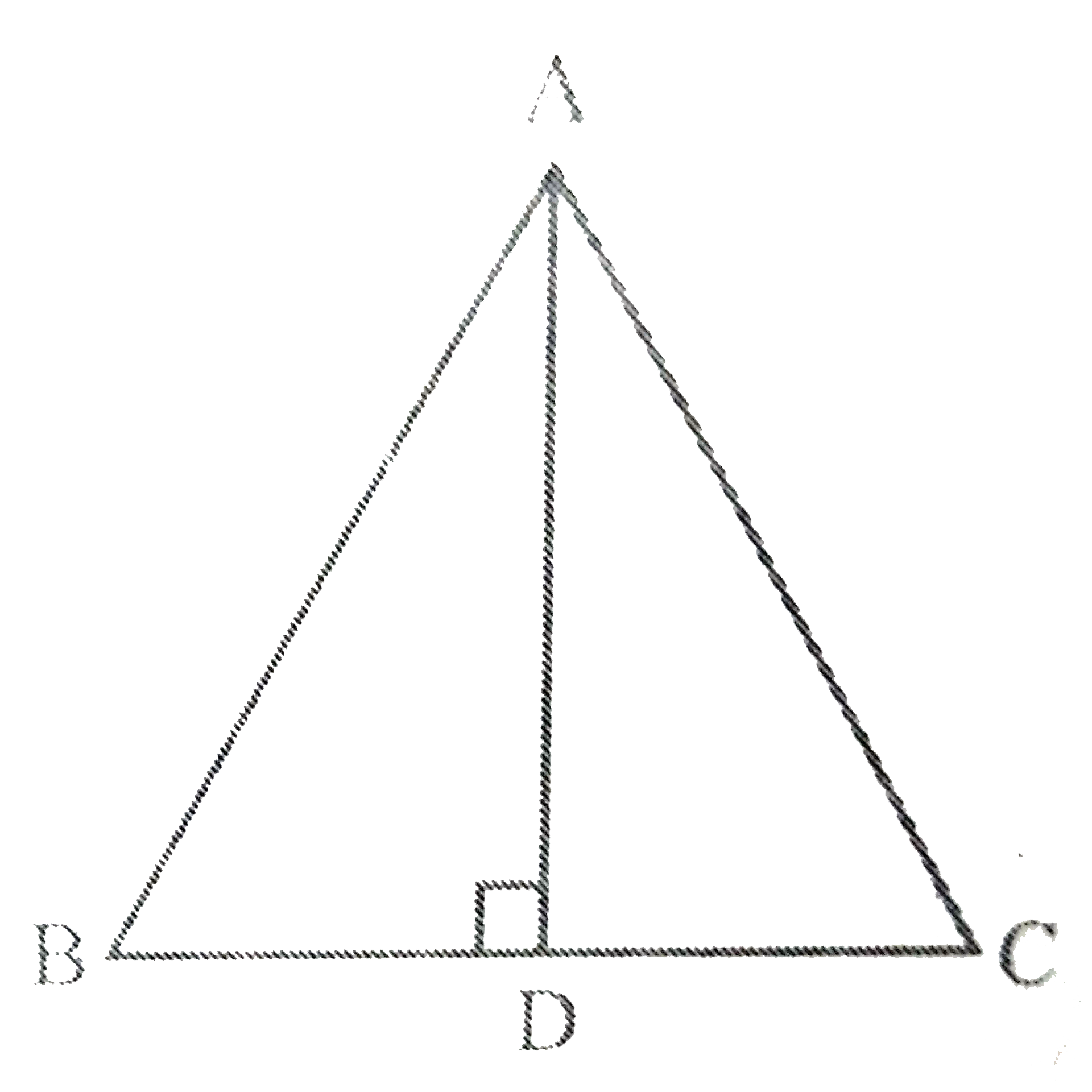
View SolutionABC एक समद्विबाहु त्रिभुज है जिसमें AC =BC है। यदि AB2=2AC2 है , तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है ।
View Solutionआकृति में त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि BDCD=ABAC है । सिद्ध कीजिए कि AD , कोण BAC का समद्विभाजन है ।
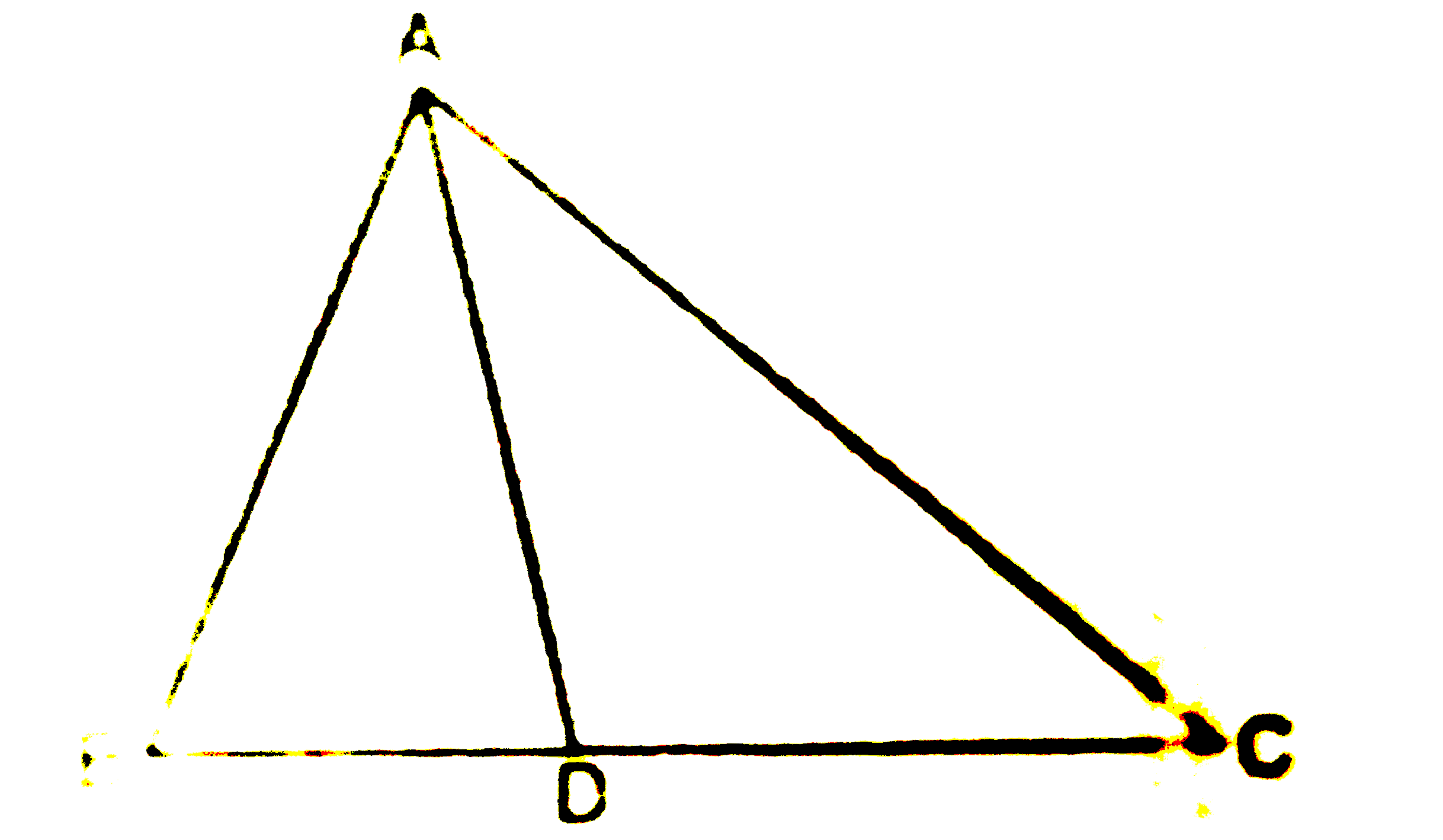
View Solution△ABC में ∠A का समद्विभाजक AD भुजा BC पर लम्ब है (आकृति देखिये) दर्शाइए की AB=AC है और △ABC समद्विभाजक है।
View Solutionयदि ABC एक समद्विबाहु त्रिभुज है तथा AC = BC यदि AB2=2AC2 है तो सिद्ध कीजिए कि △ABC एक समकोण त्रिभुज है |
View Solutionएक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AC = BC यदि AB2=2AC2 है तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है |
View SolutionABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। यदि AB2=2AC2 है, तो सिद्ध कीजिए कि त्रिभुज ABC एक समकोण त्रिभुज है।
View SolutionABC is an isoscles triangle in which AB =AC. If O be the centre of the circle and ∠OBC=30∘ then the value of ∠ABC is ________
View Solution
