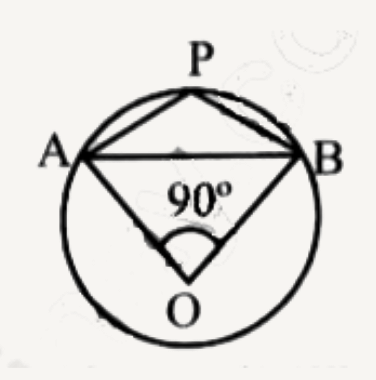
In the diagram , O is the centre of the circle and ∠OPA=30∘, Find ∠ACBand∠ADB respectively.
A
120∘,60∘
B
60∘,120∘
C
75∘,105∘
D
35∘,145∘
Video Solution
Text Solution
The correct Answer is:B
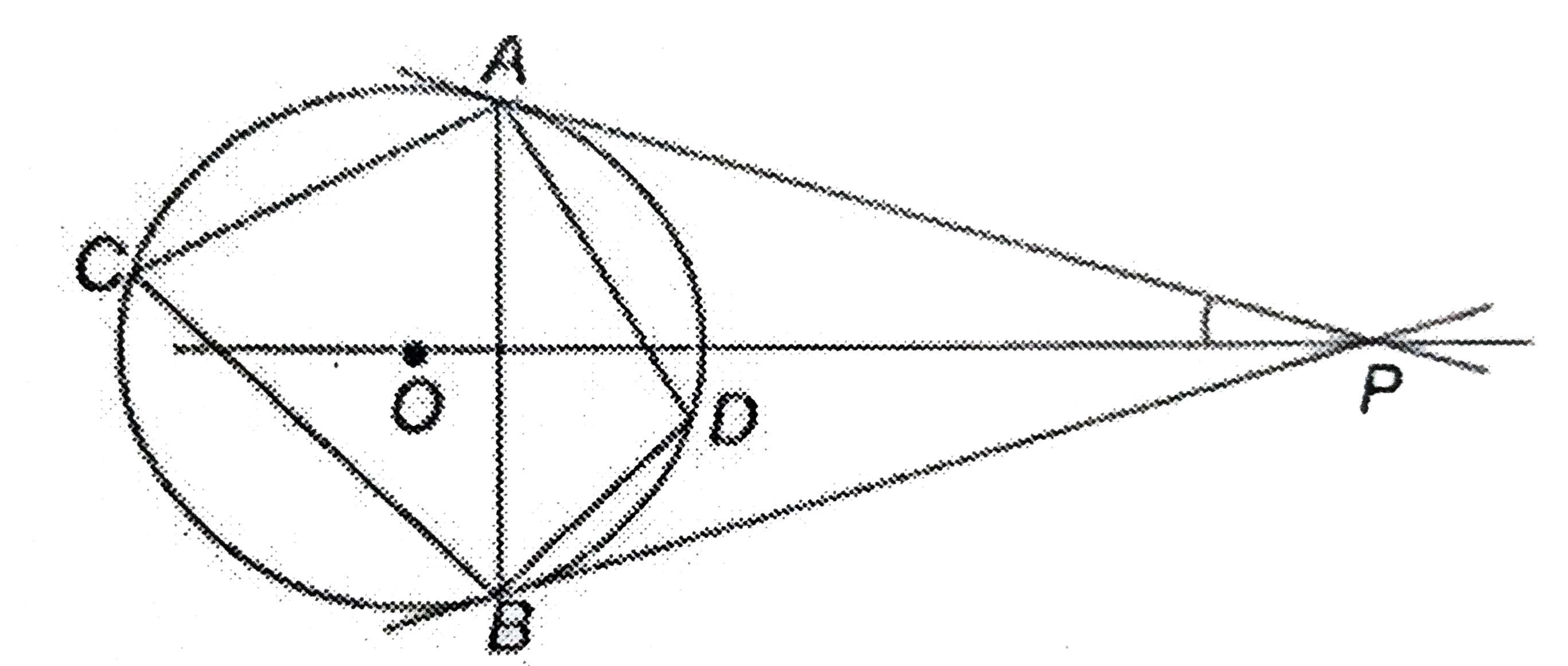
(i) Tangents drawn form an external point to the same circle are equal, i.e, PA=PB.
(ii) ∠APO=∠OPBand∠AOB+∠APB=180∘
(iii) ∠ACB=12∠AOB.
(iv) ACBD is a cyclic quadrilateral.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If O is the centre of circle and ∠ADE=60∘ then find ∠AOC
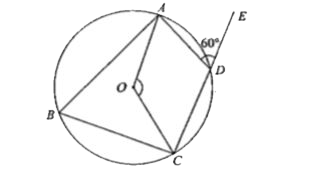 A60∘B100∘C120∘DNone of these
A60∘B100∘C120∘DNone of these - Question 2 - Select One
If O is the centre of the circle then find ∠ADC
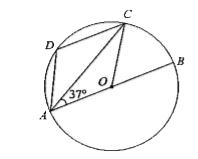 A125∘B127∘C90∘D137∘
A125∘B127∘C90∘D137∘ - Question 3 - Select One
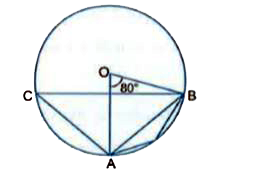
In the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.
 A=60∘B=45∘C=30∘D=50∘
A=60∘B=45∘C=30∘D=50∘

In the figure (not to scale ), O is the centre of the circle and ∠OBA=30∘. Find ∠ACBView SolutionO is the incentre of ΔABC and ∠A=30∘, then find ∠BOC.
View SolutionIn the figure, O is centre of a circle. If ∠BAC=20∘and∠ACB=30∘. Find ∠AOC
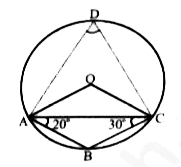 View Solution
View SolutionIn the figure, O is the centre of the circle . ∠PQR is equal to
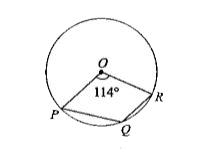 View Solution
View SolutionO is the centre of the circle, ABN is a straight line. Find ∠AOC.
 View Solution
View Solution