P,Q and R are on AB, BC and AC of the equilateral triangle ABC respectively. AP:PB=CQ:QB=1:2. G is the centroid of the triangle PQB and R is the mid-points of AC. Find BG:GR.
1:2
2:3
3:4
4:5
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Set Up the Triangle
We start by drawing an equilateral triangle ABC. Label the vertices A, B, and C.
Step 2: Mark Points P, Q, and R
According to the problem, points P, Q, and R are located on sides AB, BC, and AC respectively.
Step 3: Use Given Ratios
We are given that AP:PB=CQ:QB=1:2. This means:
- Let AP=x and PB=2x. Therefore, AB=AP+PB=x+2x=3x.
- Let CQ=y and QB=2y. Therefore, BC=CQ+QB=y+2y=3y.
Step 4: Establish Relationships
Since ABC is an equilateral triangle, all sides are equal, hence AB=BC=AC. Therefore, we have:
- 3x=3y which implies x=y.
Step 5: Calculate Lengths
Let x=y=k. Thus:
- AP=k, PB=2k, CQ=k, and QB=2k.
- The length of side AB=3k and side BC=3k.
Step 6: Locate Point R
Point R is the midpoint of AC. Since AC is also 3k, the coordinates of R will be at 3k2.
Step 7: Find Centroid G of Triangle PQB
The centroid G of triangle PQB divides each median in the ratio 2:1. To find the coordinates of G, we first need the coordinates of points P and Q.
Assuming:
- A is at (0,0)
- B is at (3k,0)
- C is at (3k2,3k√32)
Coordinates of P:
- Since AP=k, P will be at (k,0).
Coordinates of Q:
- Since CQ=k, Q will be at (3k2,3k√32−k).
Step 8: Calculate Coordinates of G
Using the formula for the centroid G:
Gx=x1+x2+x33,Gy=y1+y2+y33
Substituting the coordinates of P, Q, and B:
Gx=k+3k2+3k3=(k+1.5k+3k)3=5.5k3
Gy=0+(3k√32−k)+03=3k√32−k3=(3√3/2−1)k3
Step 9: Calculate BG and GR
To find the lengths BG and GR:
1. BG is the distance from B to G.
2. GR is the distance from G to R.
Using the distance formula, we can find these lengths.
Step 10: Find the Ratio BG:GR
Finally, we compute the ratio BGGR.
After performing the calculations, we find that:
BG:GR=4:5
Final Answer
Thus, the ratio BG:GR is 4:5.
---
We start by drawing an equilateral triangle ABC. Label the vertices A, B, and C.
According to the problem, points P, Q, and R are located on sides AB, BC, and AC respectively.
We are given that AP:PB=CQ:QB=1:2. This means:
- Let AP=x and PB=2x. Therefore, AB=AP+PB=x+2x=3x.
- Let CQ=y and QB=2y. Therefore, BC=CQ+QB=y+2y=3y.
Since ABC is an equilateral triangle, all sides are equal, hence AB=BC=AC. Therefore, we have:
- 3x=3y which implies x=y.
Let x=y=k. Thus:
- AP=k, PB=2k, CQ=k, and QB=2k.
- The length of side AB=3k and side BC=3k.
Point R is the midpoint of AC. Since AC is also 3k, the coordinates of R will be at 3k2.
The centroid G of triangle PQB divides each median in the ratio 2:1. To find the coordinates of G, we first need the coordinates of points P and Q.
- A is at (0,0)
- B is at (3k,0)
- C is at (3k2,3k√32)
- Since AP=k, P will be at (k,0).
- Since CQ=k, Q will be at (3k2,3k√32−k).
Using the formula for the centroid G:
Gx=x1+x2+x33,Gy=y1+y2+y33
Substituting the coordinates of P, Q, and B:
Gx=k+3k2+3k3=(k+1.5k+3k)3=5.5k3
Gy=0+(3k√32−k)+03=3k√32−k3=(3√3/2−1)k3
To find the lengths BG and GR:
1. BG is the distance from B to G.
2. GR is the distance from G to R.
Finally, we compute the ratio BGGR.
BG:GR=4:5
Thus, the ratio BG:GR is 4:5.
Topper's Solved these Questions
Similar Questions
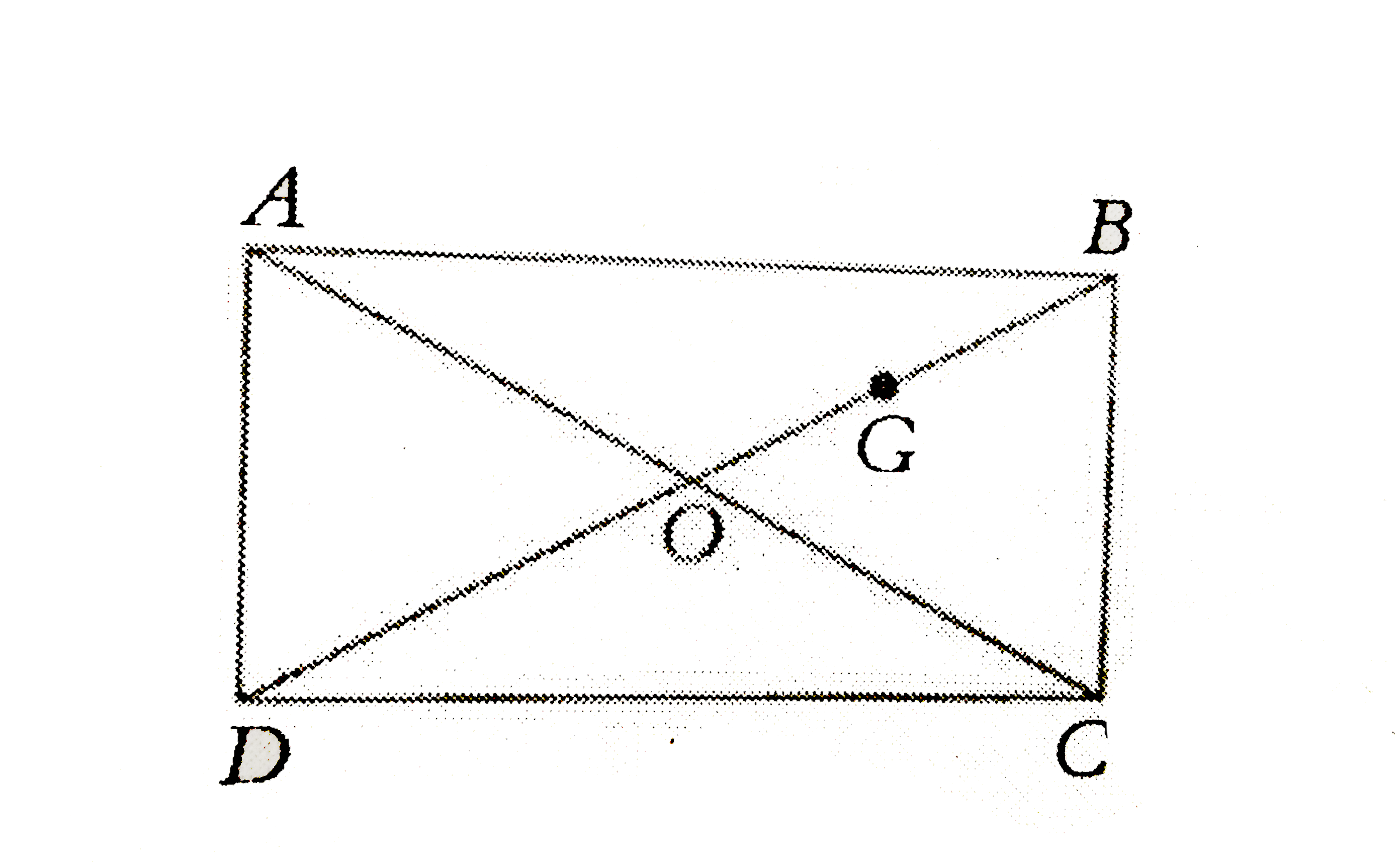
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC. If BG=4cm, then find the length of AC.
View SolutionIn a ΔABC, F and E are the mid point of AB and AC respectively. G is the centroid of ΔABC. If X, Y and Z are the mid points of EF, FG & GE respectively. Find the ratio of area of ΔXYZ to area of ΔABC.
View Solution
Knowledge Check
The mid-points of sides AB and AC of a triangle ABC are respectively X and Y. If (BC+XY)=12units, then the value of (BC−XY) is :
A2 unitsB6 unitsC8 unitsD4 unitsThe mid-points of sides AB and AC of a triangle ABC are respectively X and Y. If (BC+XY)=12 units, then the value of (BC−XY) is
A2 unitsB6 unitsC8 unitsD4 unitsIf ABC is an equilateral triangle and P, Q, R respectively denote the middle points of AB, BC, CA then.
APQR must be an equilateral triangleBPQ+QR+PR=ABCPQ+QR+PR=2ABDPQR must be a right angled triangle
Three forces P, Q, R act along the sides BC, AC and BA of an equilateral triangle. If their resultant is a force parallel to BC through the centroid of the triangle, prove that
Q=R=P/2
View Solution
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC . If BG=4 cm, then find the length of AC.
View SolutionIn a triangle ABC ,if the centroid is (2,0) and the mid point of BC is (1,3) then A=
View SolutionIn ΔABC,G is the centroid , AB=15cm, BC=18 cm, and AC=25 cm . Find GD , Where D is the mid point of BC:
View SolutionIn ΔABC, AB = 7 cm, BC = 24 cm and AC = 25 cm. If G is the centroid of the triangle, then what is the length (in cm) of BG?
View Solution
