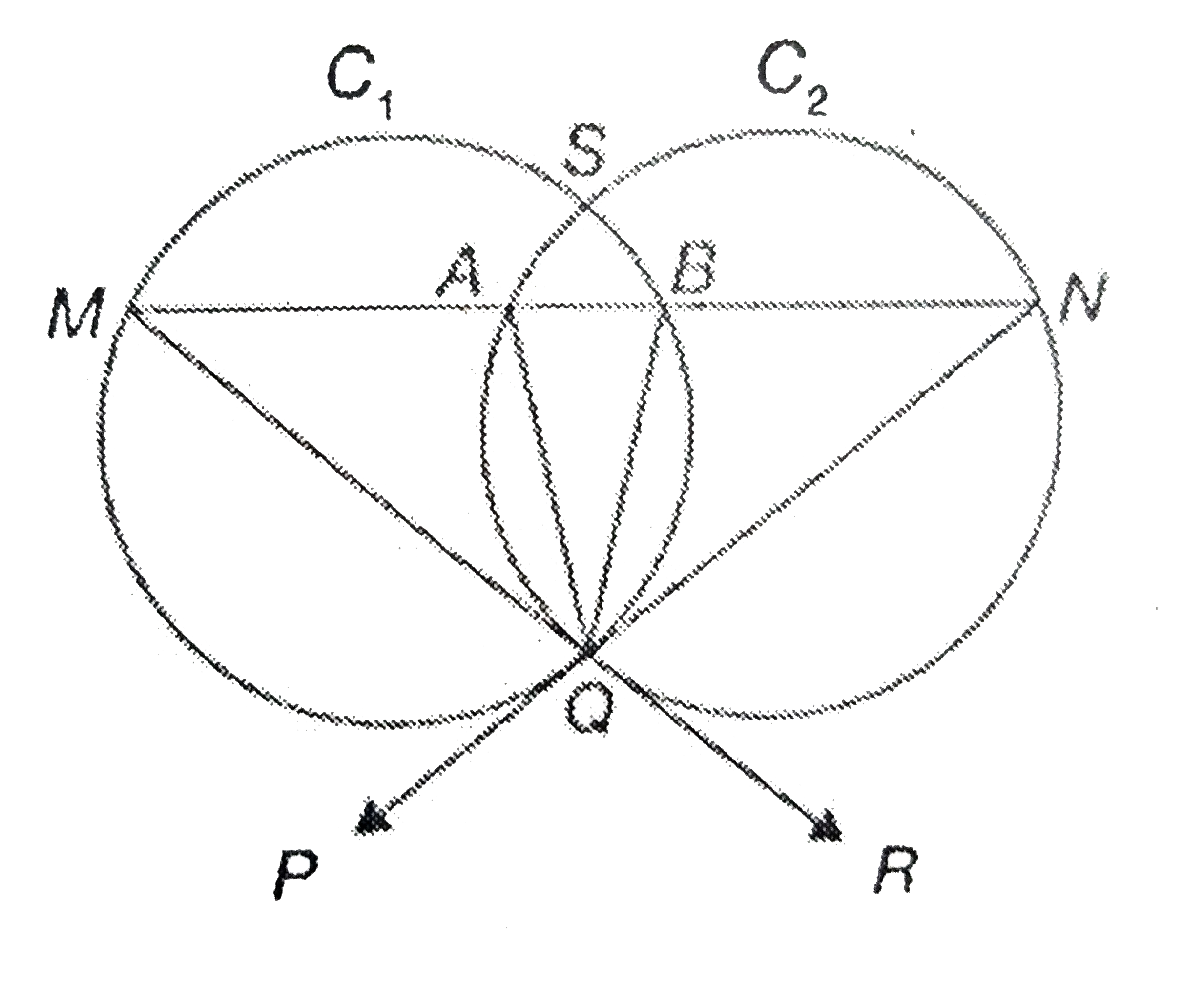
In the given figure (not to scale), two circles C1andC2 intersect at S and Q. PQN and RQM are tangents drawn to C1andC2 respectively at Q. MAB and ABN are the chords of the circles C1andC2. If ∠NQR=85∘, then find ∠AQB.
5∘
10∘
15∘
Cannot be determined
The correct Answer is:B
Given ∠NQR=85∘
But ∠NQR=∠MQP(∵Vertically opposite angles)
∴∠MQP=85∘
By alternate semgent theorem ∠NQR=∠QAB
∴∠MQP=85∘and∠MQP=∠QBA
∴∠QBA=85∘
In ∠AQB,∠AQB=180∘−(85∘+85∘)=10∘
Topper's Solved these Questions
Similar Questions
In the following figure, (not a scale), AB is the common tangent to the circles C1andC2 and C1andC−2 are touching externally at C. AD and DC are two chords of the circle, C1andBEandCE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC.
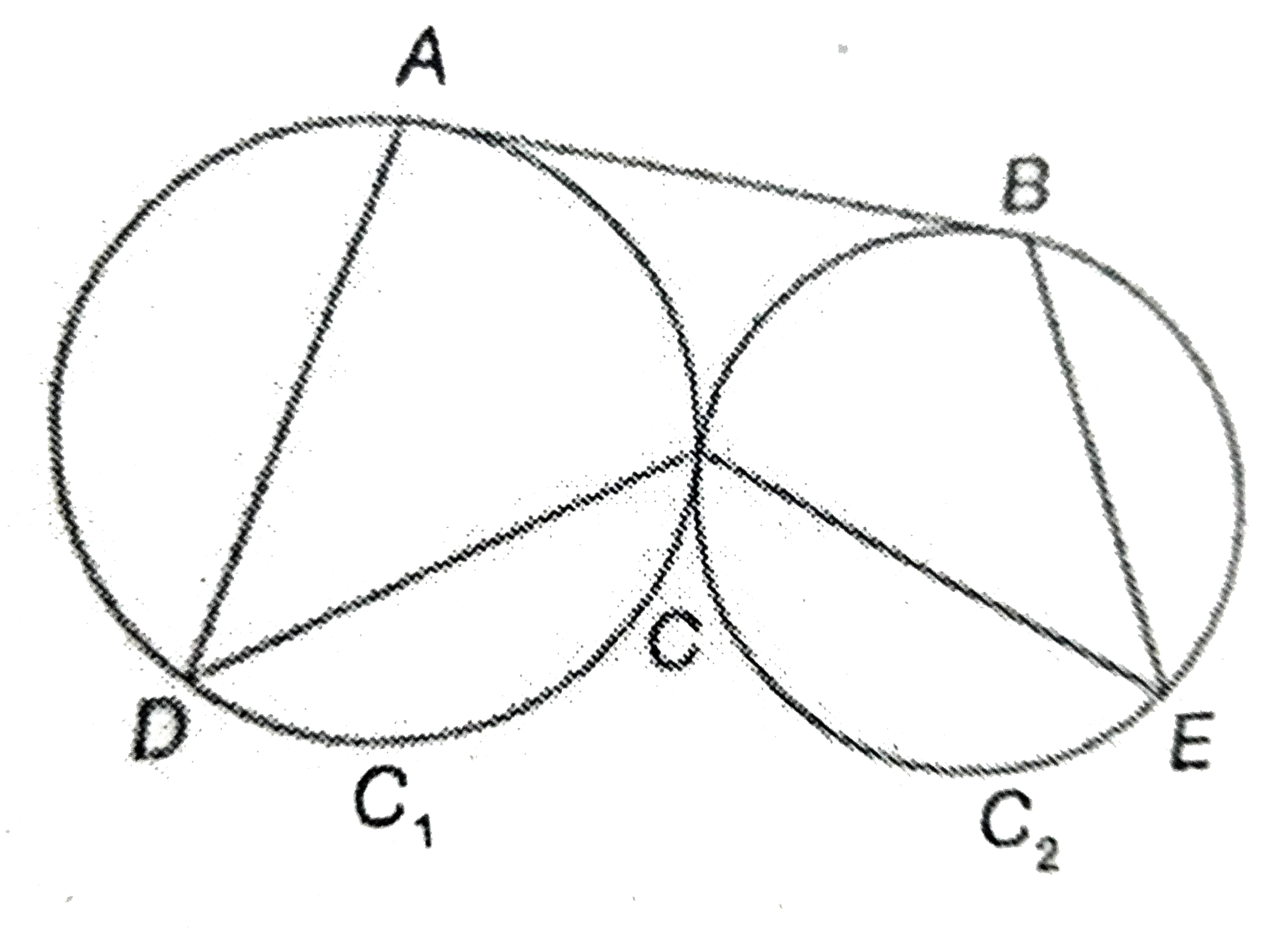
View SolutionAB is the common tangent to the circles C1 and C2. C1 and C2 are touching externally at C.AD and DC are two chords of the circle C1 and BE and CE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC
View Solution
Knowledge Check
Two circles with centres P and Q intersect at B and C, A, D are points on the circles with centres P and Q respectively such that A, C, D are colliner. If ∠APB=130∘,and∠BQD=x∘, then the value of x is :
A65B130C195D135In the arrangement shown in figure dielectric constant K1=2 and K2=3. If the capacitance across P and Q are C1 and C2 respectively, then C1/C2 will be (the gaps shown are negligible)
 A1:1B2:3C9:5D25:24
A1:1B2:3C9:5D25:24C1andC2 are two circle which touch internally at point P. Two lines PCA and PDB meet circle C1 at C and D and circle C2 at A and B respectively. If ∠BDC=120∘ then what is value of ∠ABP. (If CD||AB)
A60∘B80∘C100∘D120∘
If tangent at (1,2) to the circle x2+y2=5 intersect the circle x2+y2=9 at A and B and tangents at A and B meets at C. Find the coordinate of C
View SolutionTwo circles C1andC2 with equal radii r are centered at (3,2)and(6,5) respectively. If C1andC2 intersect orthogonally, then r is equal to.
View SolutionIn the given figure (not to scale), O is the center of the circle C1 and AB is the diameter of the circle C2. Quadrilateral PQRS is inscribed in the circle with center O. Find ∠QRS.
View SolutionTransverse common tangents are drawn from O to the two circles C1,C2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C1andC2 and chord of contacts of O w.r.t the circles C1andC2 respectively is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View Solution
