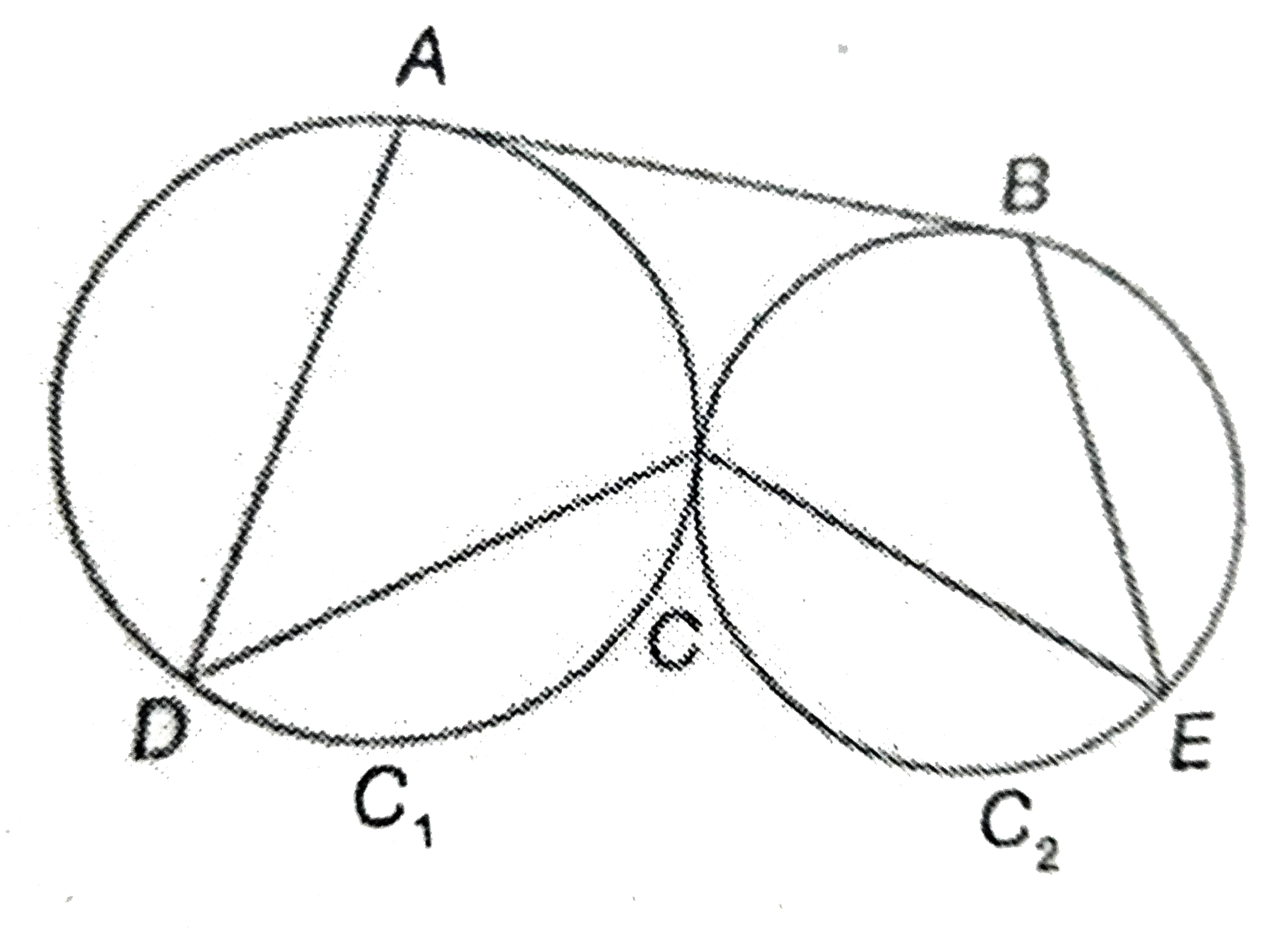
In the following figure, (not a scale), AB is the common tangent to the circles C1andC2 and C1andC−2 are touching externally at C. AD and DC are two chords of the circle, C1andBEandCE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC.
60∘
90∘
120∘
100∘
The correct Answer is:B
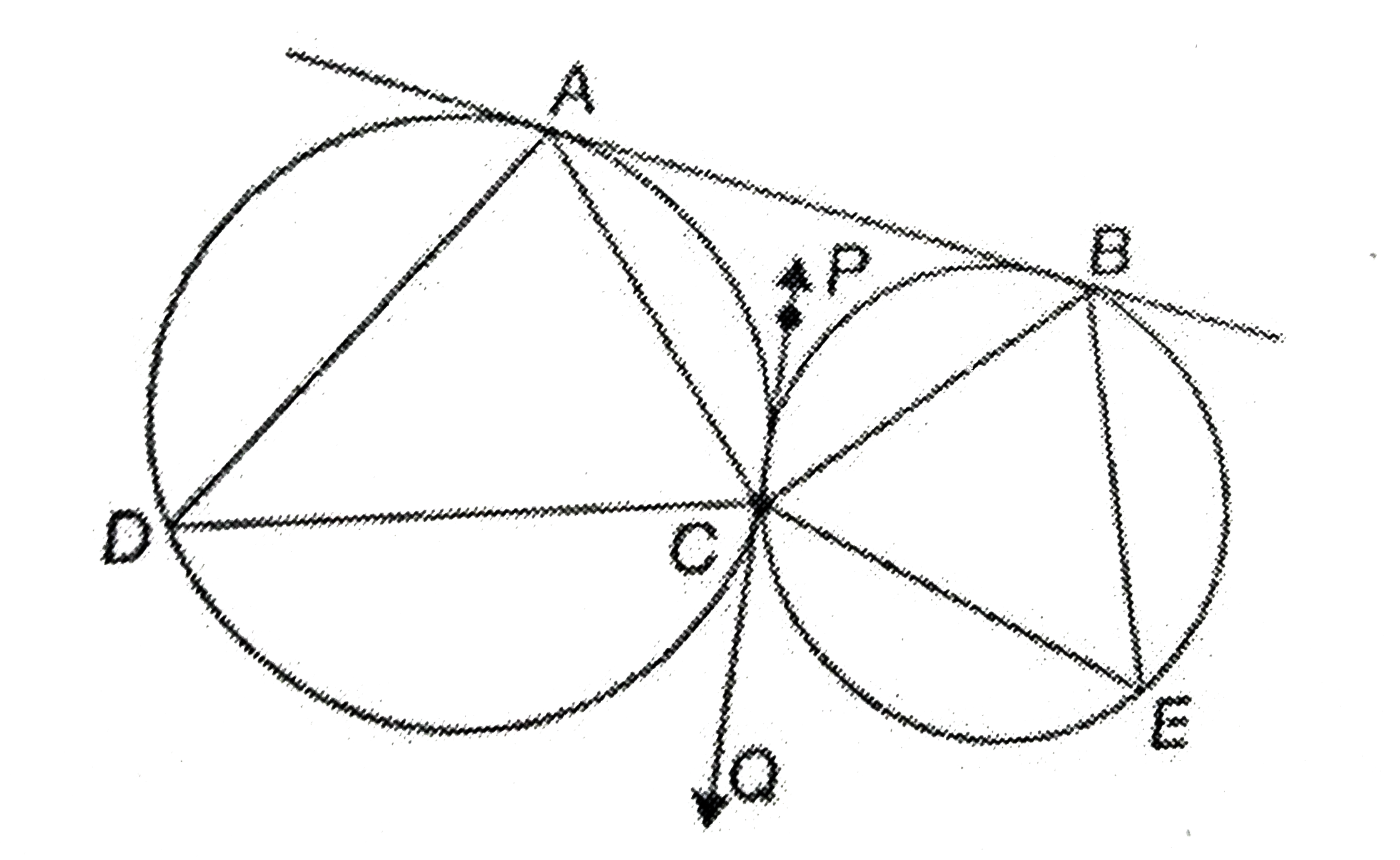
Join AC and BC
Draw a common tangent to the circles through the point C.
Let
∠ADC=xand∠BEC=y(1)
By alternate segment theorem. ∠ADC=∠BAC,∠ADC=∠ACP
∴∠BAC=∠ACP=X
and also ∠BEC=∠CBA,∠BEC=∠BCP
∴∠CBA=∠BCP=Y
In ΔABC,∠BAC+∠CBA+∠ACB=180∘
x+y+(x+y)=180∘⇒x+y=90∘(2)
From (1) and (2) , we have
∠ADC+∠BEC=90∘
Topper's Solved these Questions
Similar Questions
AB is the common tangent to the circles C1 and C2. C1 and C2 are touching externally at C.AD and DC are two chords of the circle C1 and BE and CE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC
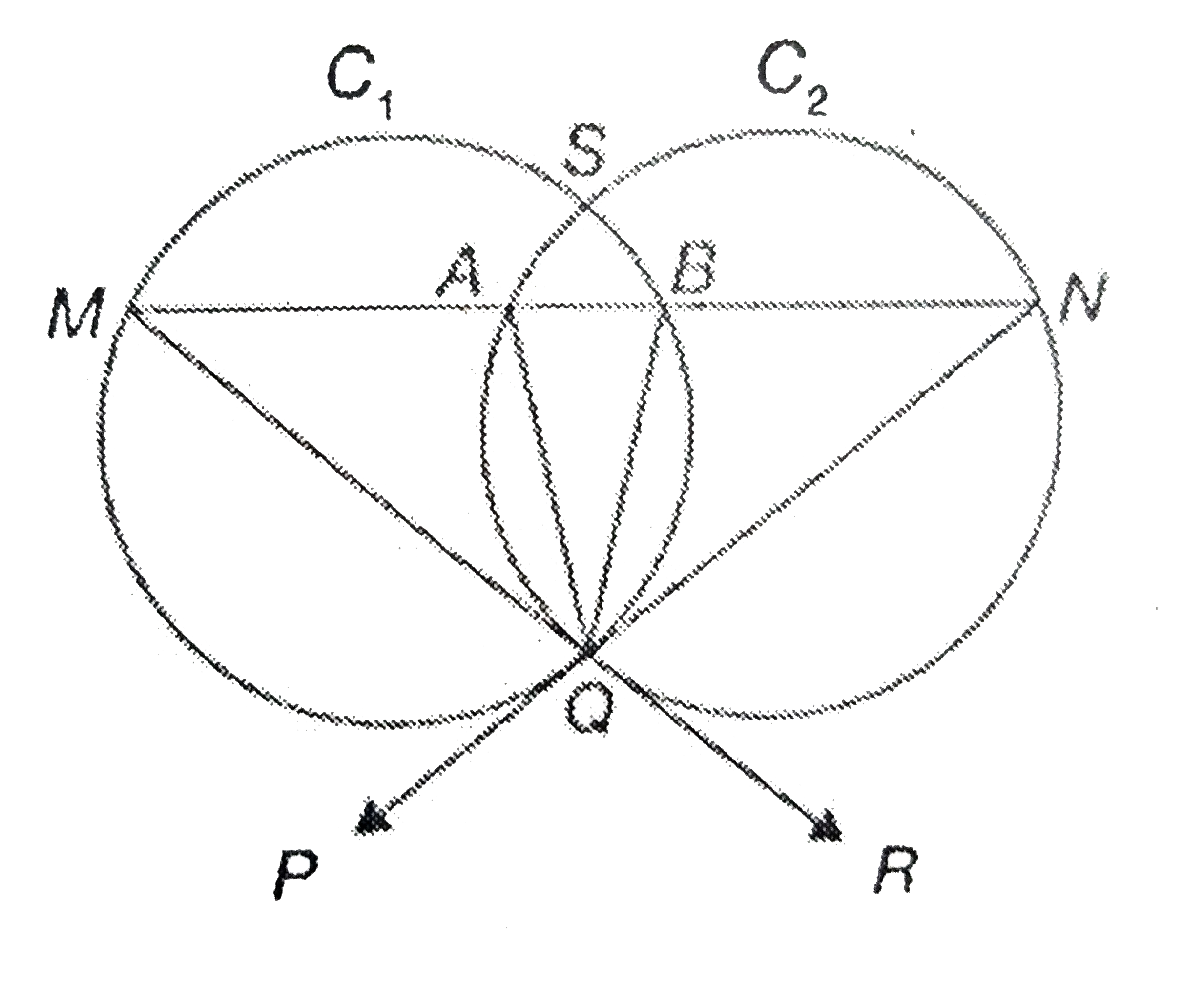
View SolutionIn the given figure (not to scale), two circles C1andC2 intersect at S and Q. PQN and RQM are tangents drawn to C1andC2 respectively at Q. MAB and ABN are the chords of the circles C1andC2. If ∠NQR=85∘, then find ∠AQB.
View Solution
Knowledge Check
Suppose that two circles C1 and C2 in a plane have no points in common. Then
Athere is no line tangent to both C1 and C2Bthere are exactly four lines tangent to both C1 and C2Cthere are no lines tangent to both C1 and C2 or there are exactly two lines tangent to both C1 and C2Dthere are no lines tangent to both C1 and C2 or there are exactly four lines tangent to both C1 and C2Circles C(o, r) and C(O1,r2) touch internally at a point A and AB is a chord of the circle intersecting C(O1,r2) at C. Then AC is equal to :
ACBBOACOBD13 ABC1andC2 are two circle which touch internally at point P. Two lines PCA and PDB meet circle C1 at C and D and circle C2 at A and B respectively. If ∠BDC=120∘ then what is value of ∠ABP. (If CD||AB)
A60∘B80∘C100∘D120∘
In the following figure, AB is an arc of the circle, C and D are the points on the circle. If ∠ACB=30∘, Find ∠ADB.

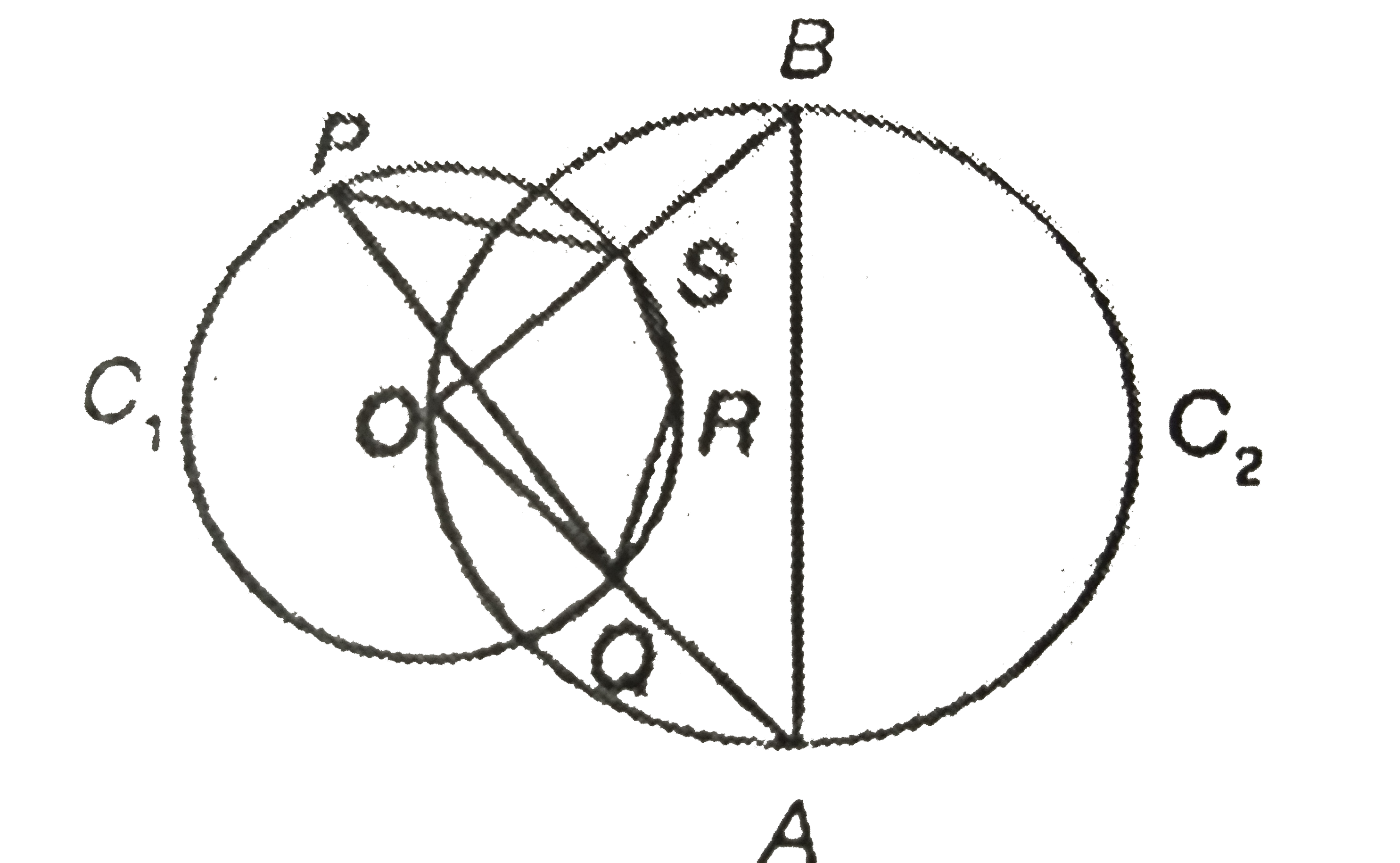
View SolutionIn the given figure (not to scale), O is the center of the circle C1 and AB is the diameter of the circle C2. Quadrilateral PQRS is inscribed in the circle with center O. Find ∠QRS.
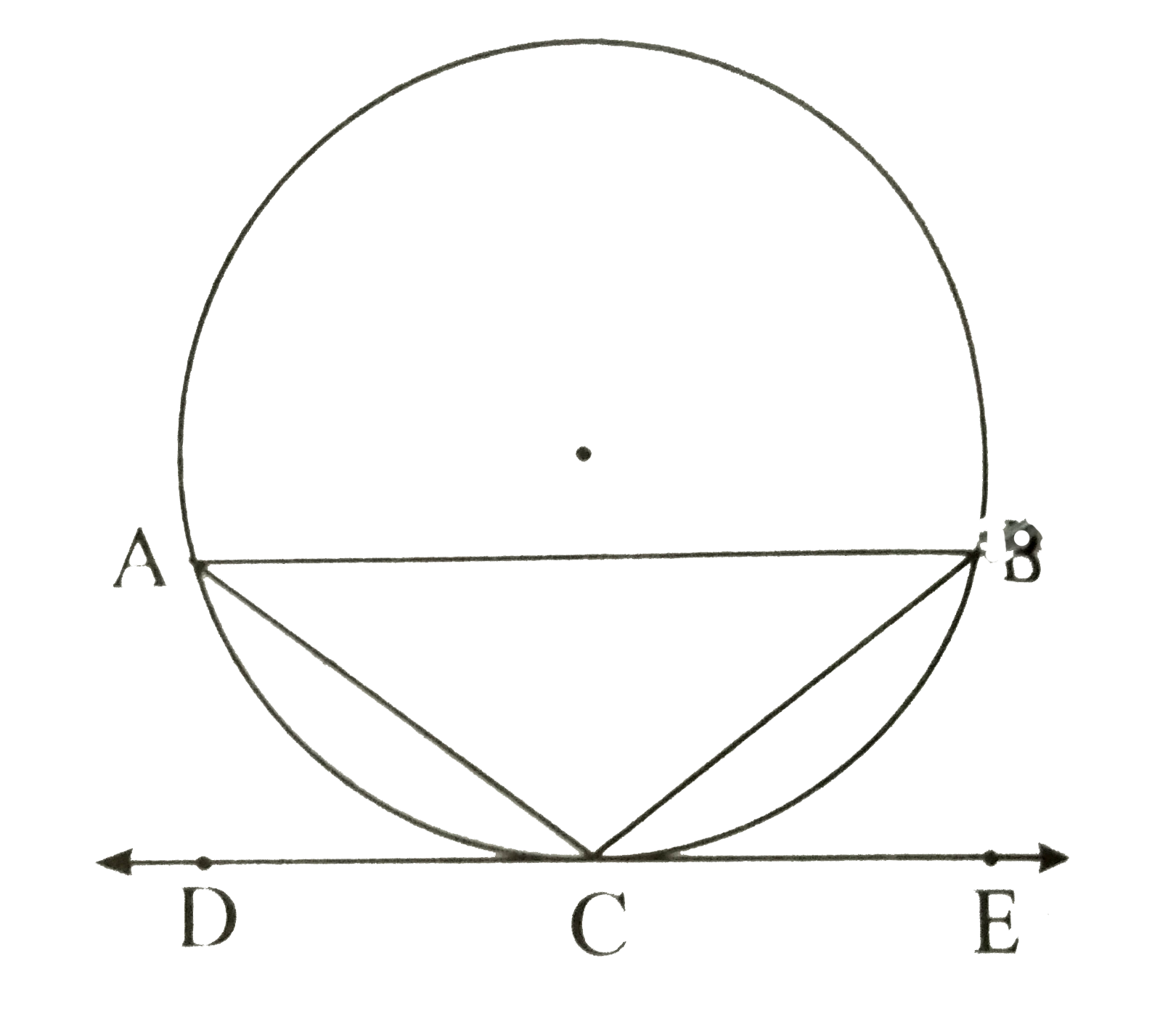
View SolutionIn the figure, chord AB∣∣ tangent DE. Tangent DE touches the circle at point C then prove AC = BC.
View SolutionTwo circles with radii a and b respectively touch each other externally . Let c be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then
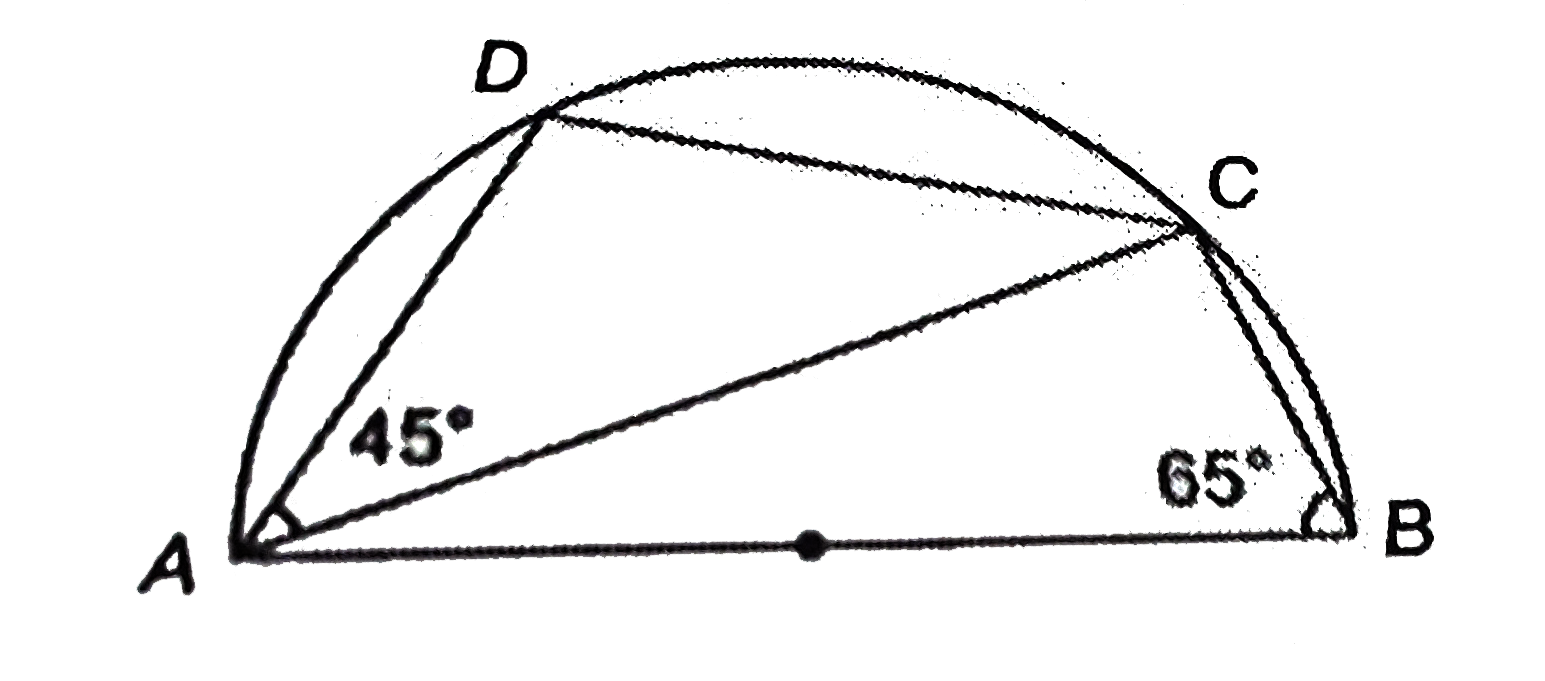
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
View Solution
