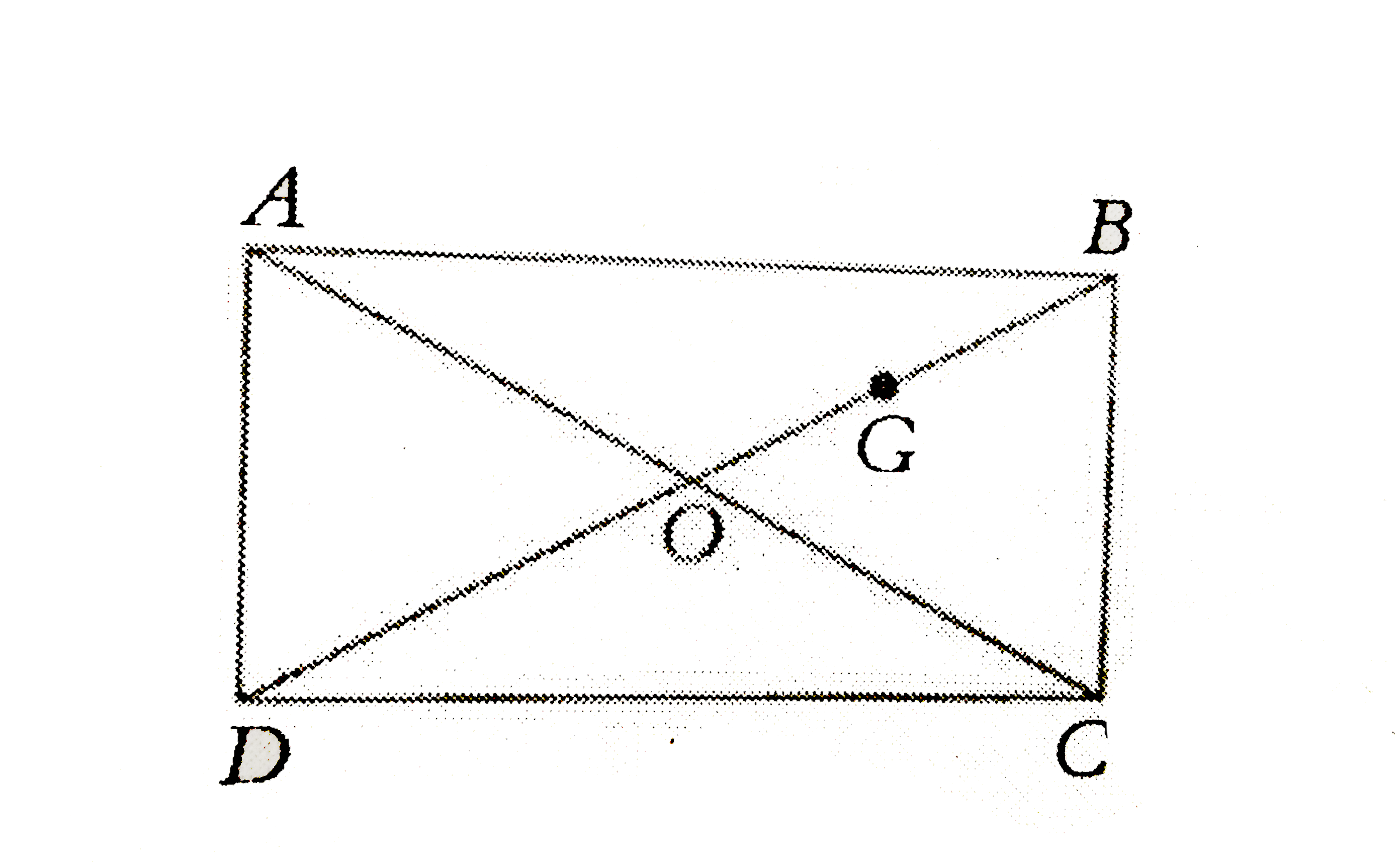
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC. If BG = 4 cm, then find the length of AC.
In the figure, ABCD is a rectangle and G is the centroid of the triangle ABC. If BG=4cm, then find the length of AC.

A

12 cm

B

13 cm

C

14 cm

D

15 cm

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

We know that, the centroid of a triangle divides each median in the ratio of 2:1 from the vertex.
Given, BG=4cm.
OG=12(4cm)=2cm
⇒BO=BG+OG=6cm
⇒BO=OD(∴ Diagonals bisect each other ).
⇒OD=6cm
BD=BO+OD=6cm+6cm=12
But AC=BD (∴ Diagonals are equal .)
⇒AC=12cm

Updated on:21/07/2023
|
Class 7MATHSGEOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the centroid of triangle ABC is G and BG = 9 cm, then what will be the length (in cm) of median BE?

    A12
    B14
    C15
    D13.5

  • If the centroid of triangle ABC is G and BG = 9 cm, then what will be the length (in cm) of median BE?

    A12
    B14
    C15
    D13.5

  • If distance of centroid of triangle ABC from vertex A is 6 cm them find the length of median through point, A.

    A(a) 7cm
    B(b) 9 cm
    C(c) 10cm
    D(d) 12cm