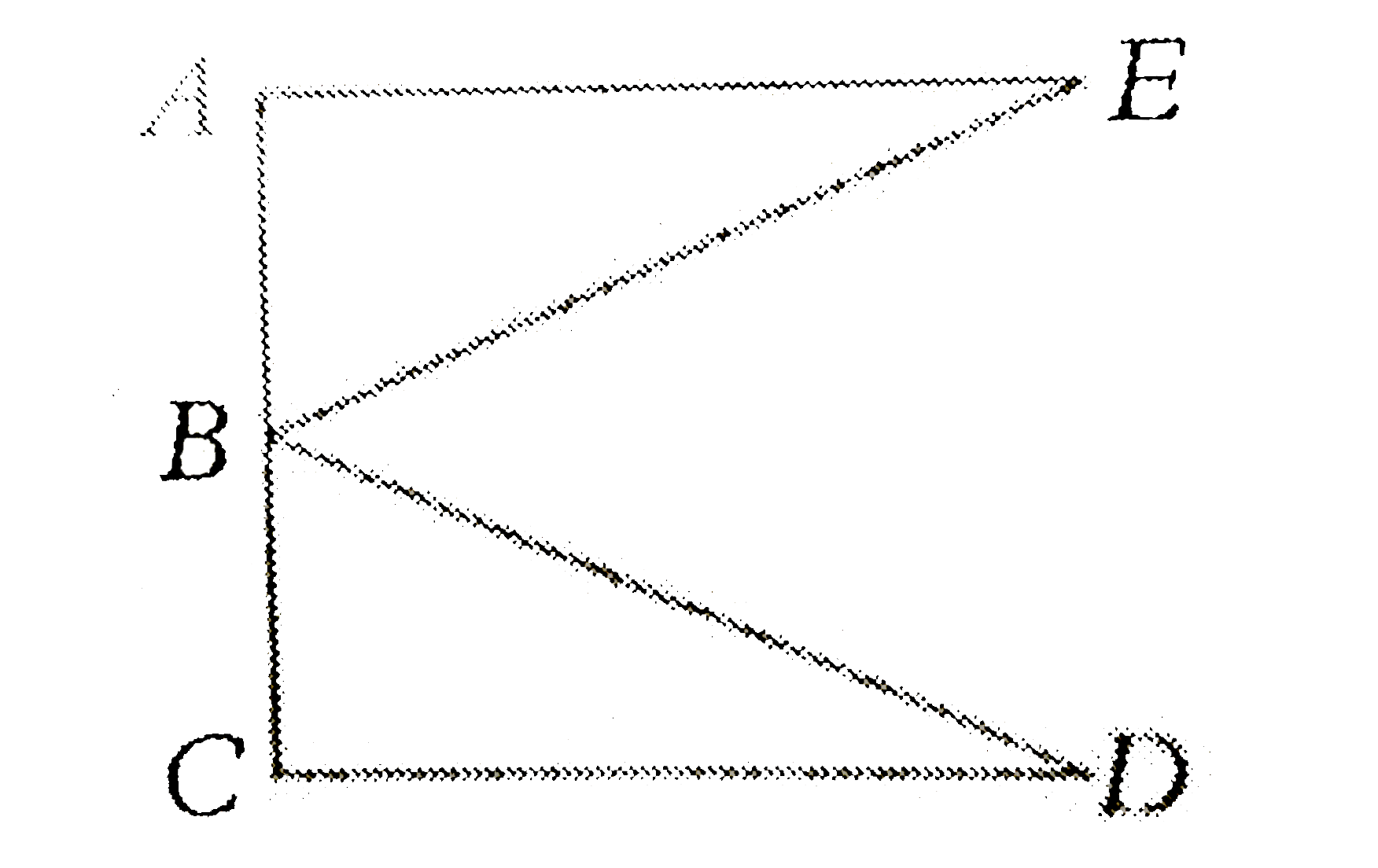
In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.
A
70∘
B
65∘
C
55∘
D
50∘
Video Solution
Text Solution
The correct Answer is:A
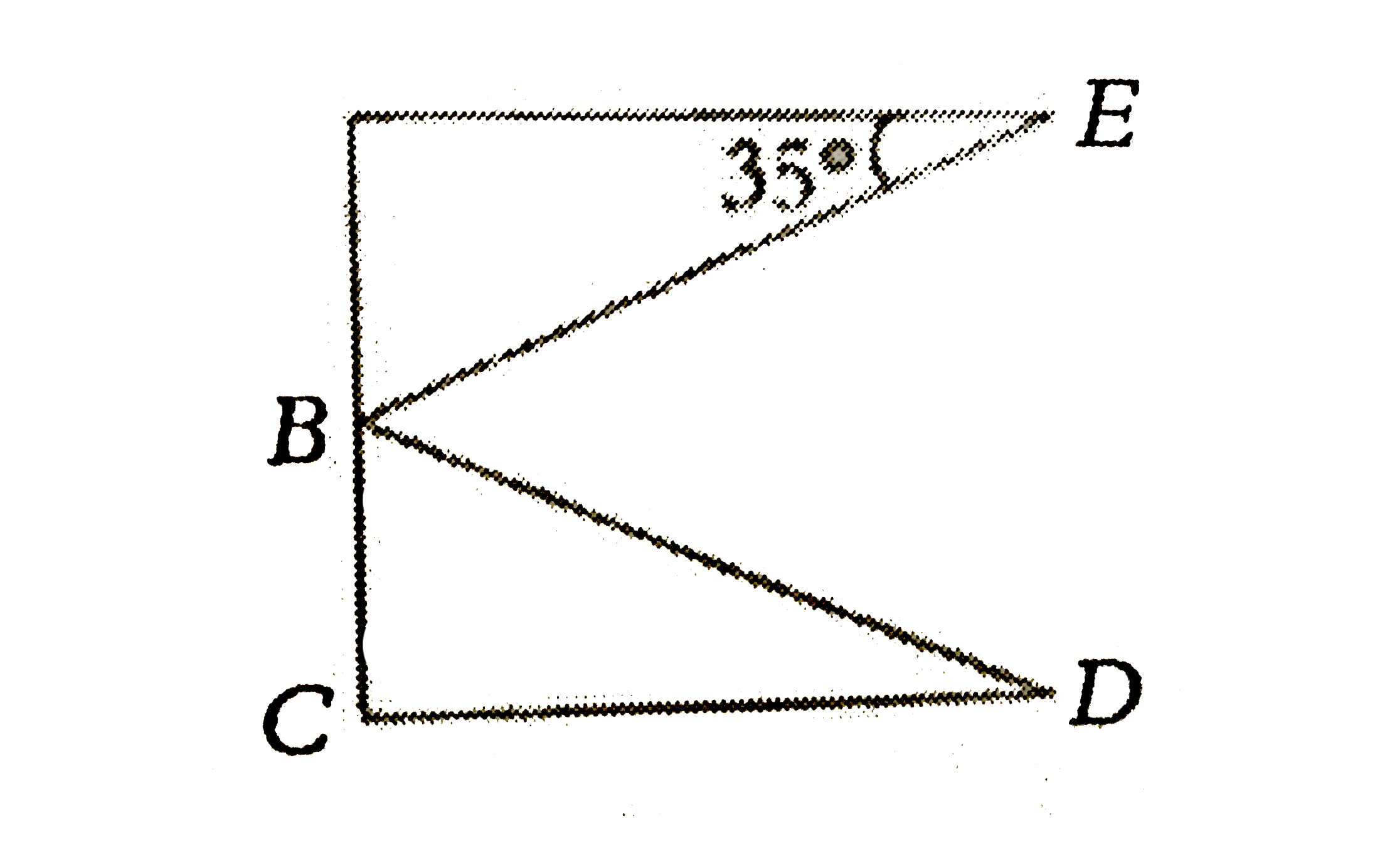
Since ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CD,∠BAE=90∘.
⇒∠ABE=180∘−90∘−35∘=55∘
( ∵¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD,¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CD )
ΔABE≅ΔCBD
∠ABE=∠CBD=55∘
∠DBE=150∘−(55∘+55∘)=70∘
Hence, the correct option is (a).
|
Topper's Solved these Questions
Similar Questions
Knowledge Check

In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.A70∘B65∘C55∘D50∘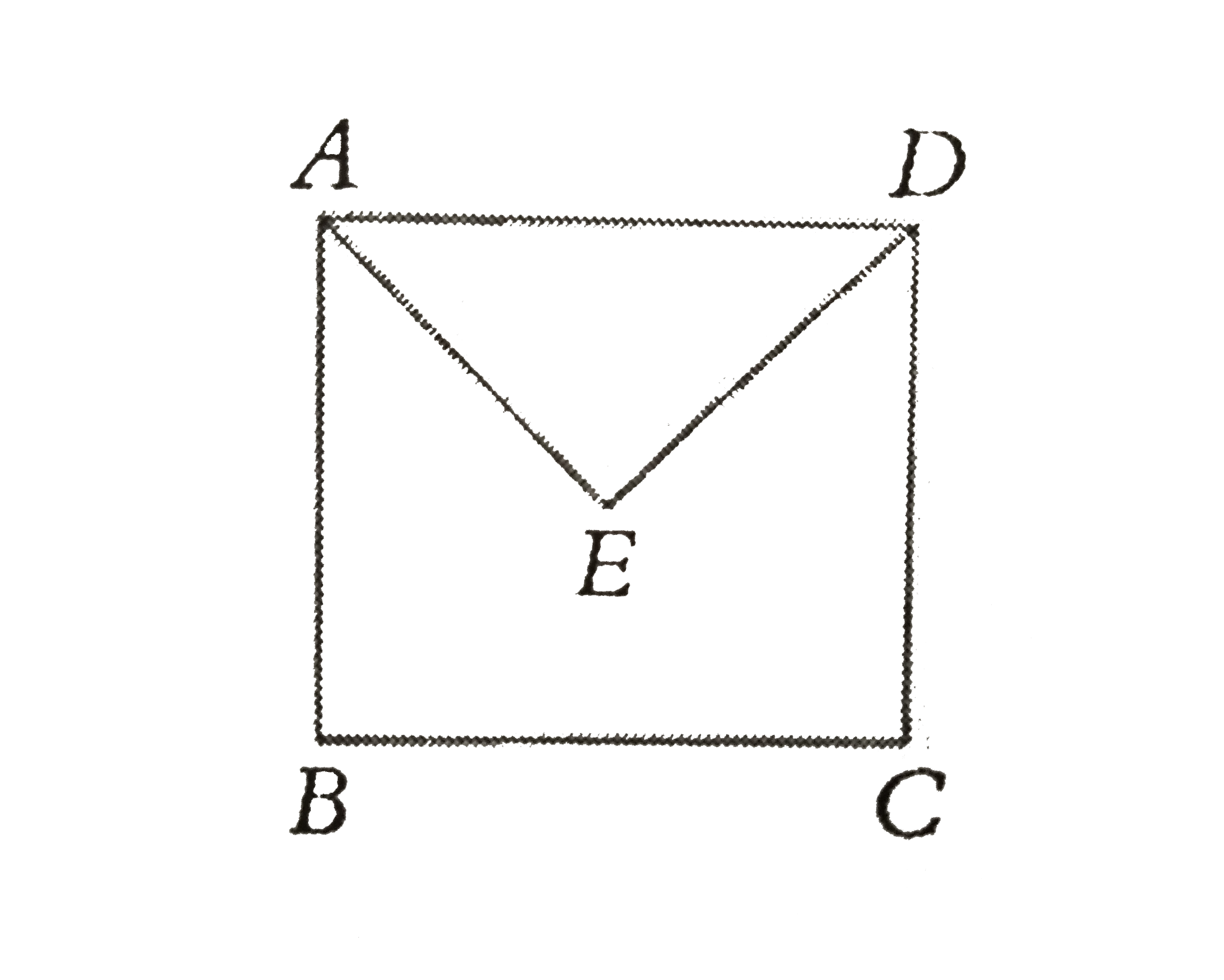
In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD,∠BAE=30∘ and ∠CDE=35∘. If ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯BC, then find ∠AED.A60∘B55∘C65∘D85∘
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘

In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD,∠BAE=30∘ and ∠CDE=35∘. If ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯BC, then find ∠AED.
View SolutionIn the given figure ¯¯¯¯¯¯AB=¯¯¯¯¯¯BC and ¯¯¯¯¯¯AC=¯¯¯¯¯¯CD if ∠BAD=y and ∠ADB=x then ∠y=
View SolutionIn the following figure (not to scale), ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠BAE=25∘ and ∠DCE=30∘, then find ∠AEC.
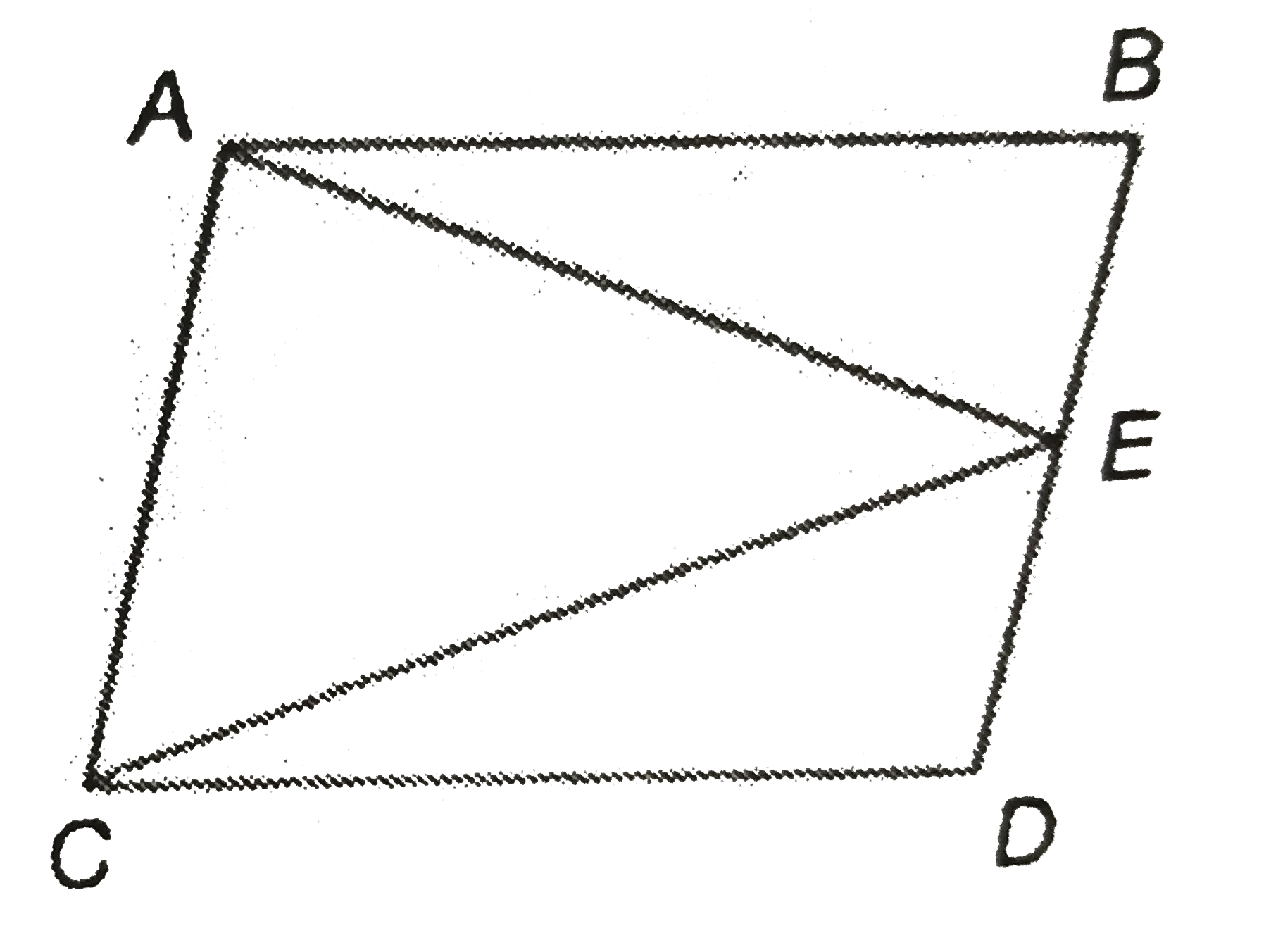
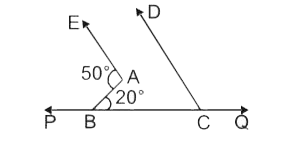
View SolutionIn the given figure find ∠DCB if AE||CD
View Solution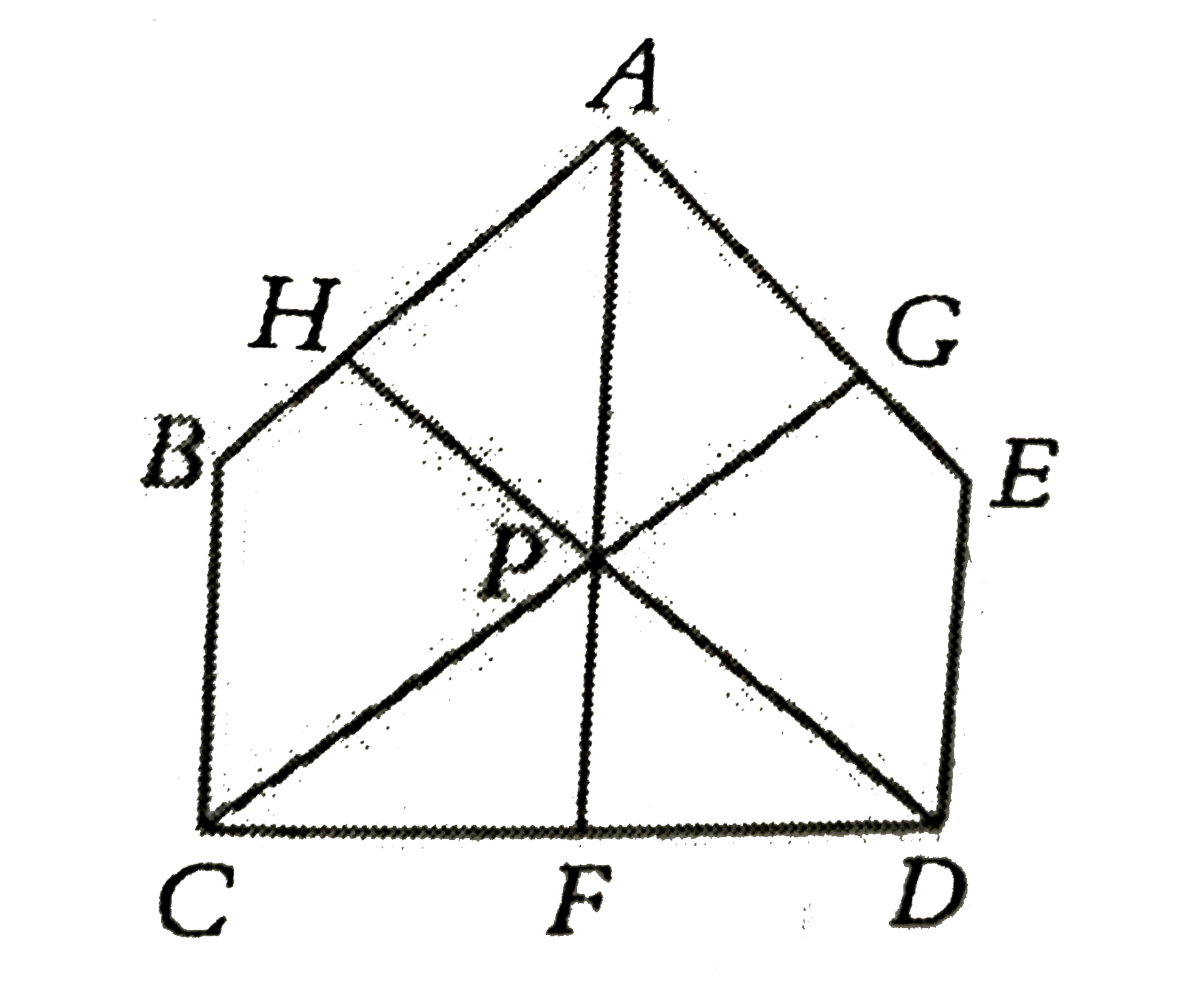
In the above figure, ¯¯¯¯¯¯AF∣∣∣∣¯¯¯¯¯¯ED,¯¯¯¯¯¯CG∣∣∣∣¯¯¯¯¯¯AB and ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯¯HD If ∠FPD=40∘, then ∠AED=
View Solution


