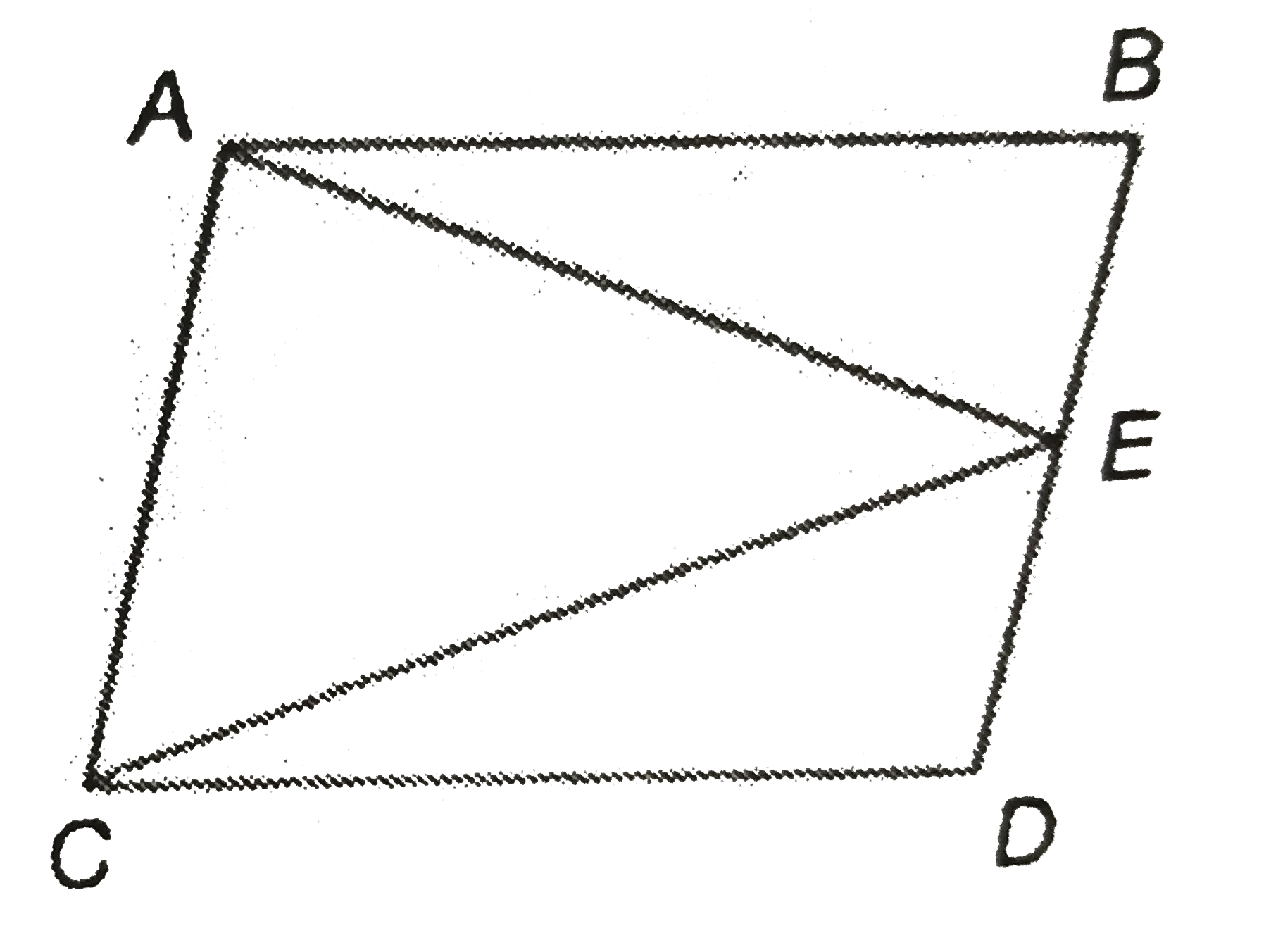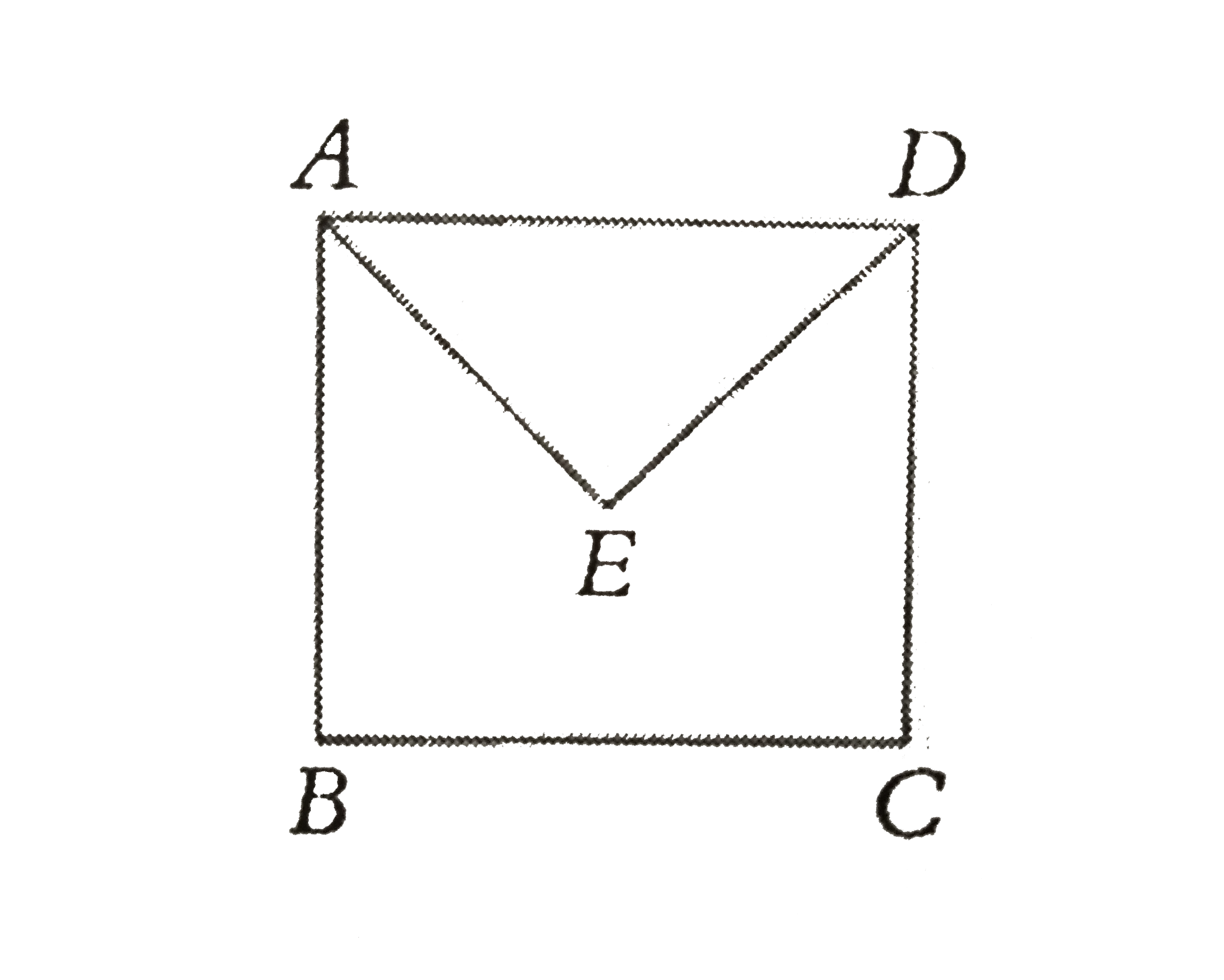
In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD,∠BAE=30∘ and ∠CDE=35∘. If ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯BC, then find ∠AED.
A
60∘
B
55∘
C
65∘
D
85∘
Video Solution
Text Solution
The correct Answer is:C
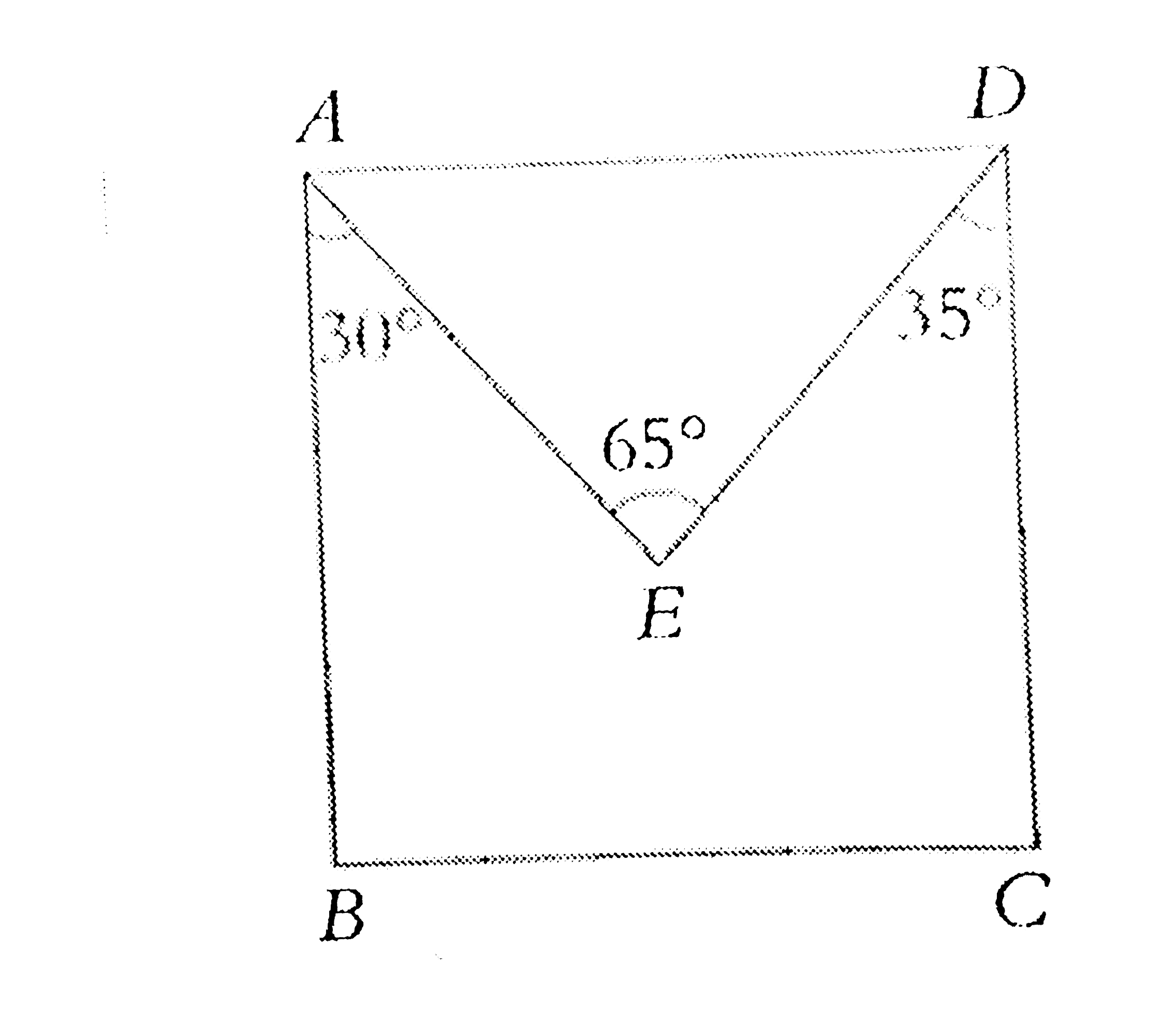
Since ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CDand¯¯¯¯¯¯AB⊥¯¯¯¯¯¯BC,∠B=∠C=90∘.
⇒∠BAD+∠CDA=180∘
∴∠EAD+∠EDA=180∘−65∘
Now, ∠AED=180−(180∘−65∘)=65∘.
Hence, the correct option is (c ).
|
Topper's Solved these Questions
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Test-2
12 Videos
- GEOMETRY BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - GEOMETRY EXERCISE - Level-3
19 Videos
- FORMULASBOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FORMULASEXERCISE - ASSESSMENT TESTS (Test 2)
8 Videos
- INDICES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - INDICES EXERCISE - Test -2
12 Videos
Similar Questions
Knowledge Check

In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD,∠BAE=30∘ and ∠CDE=35∘. If ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯BC, then find ∠AED.A60∘B55∘C65∘D85∘
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘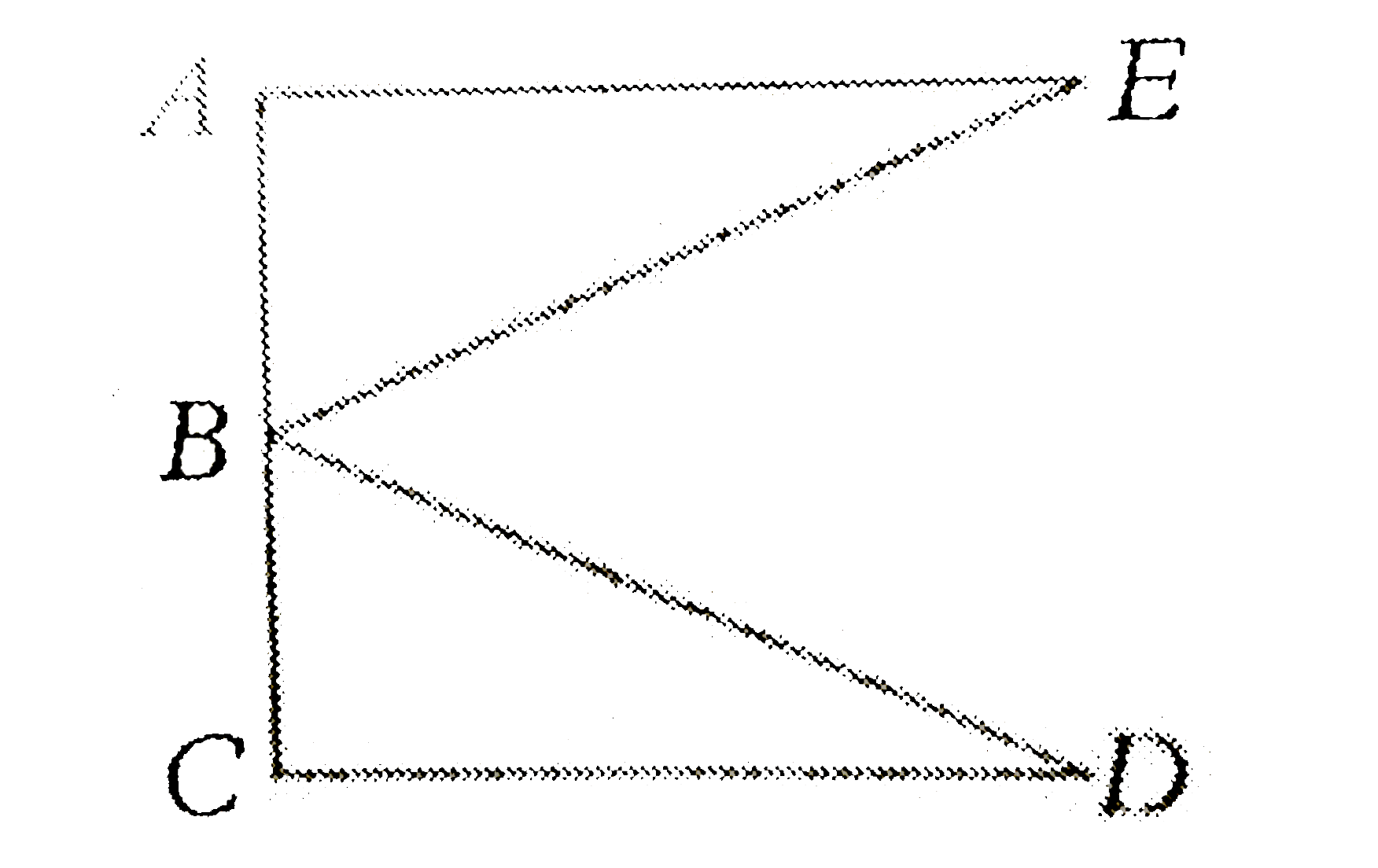
In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.A70∘B65∘C55∘D50∘
In the figure, ¯¯¯¯¯¯DC || ¯¯¯¯¯¯AB. If ∠ACB=40∘ and ∠CAD=30∘, AC is the bisector of ∠DAB, then find the angle of ∠ADC.
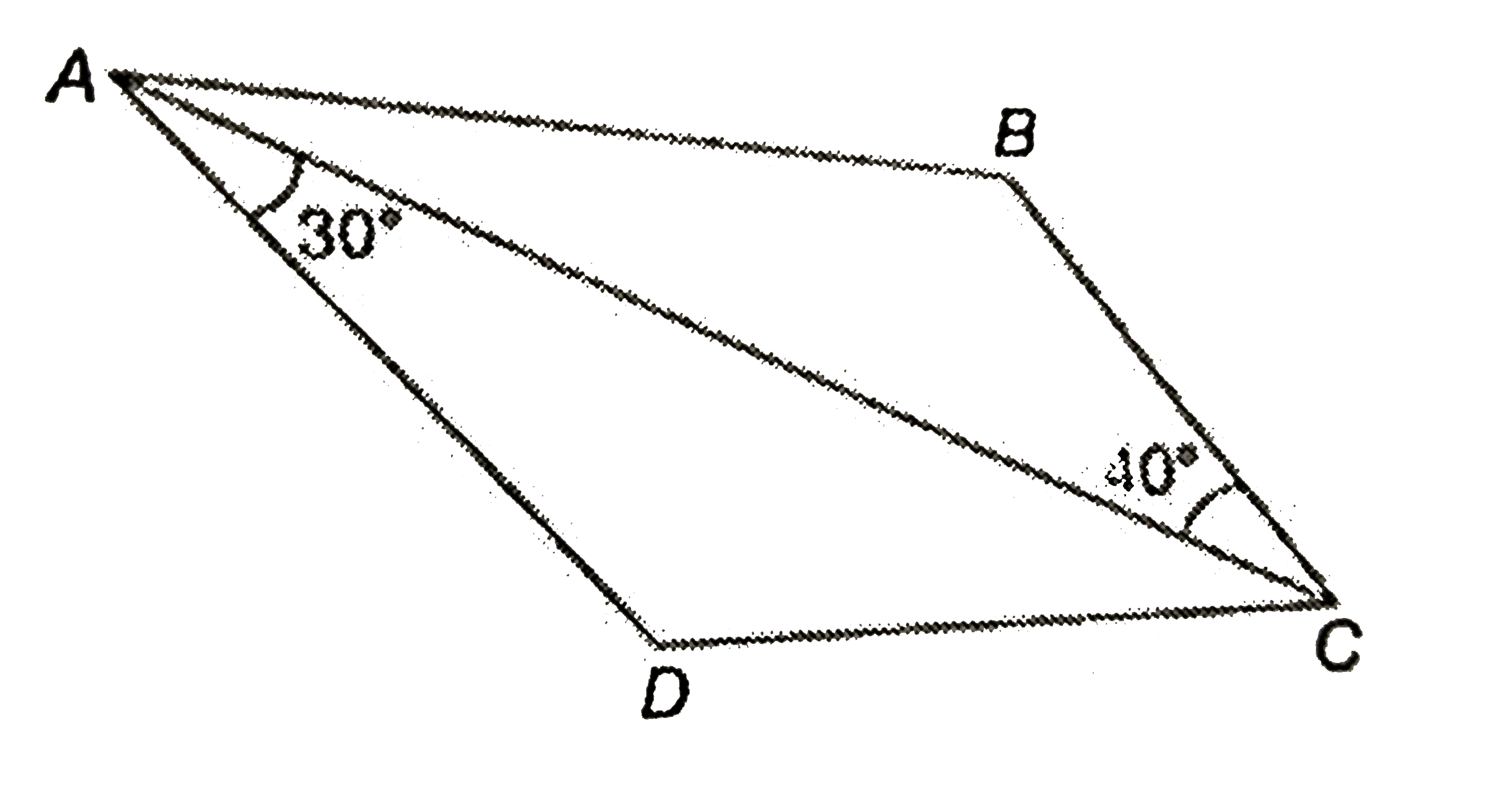
View Solution
In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.
View SolutionFind m∠C in the given figure if ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯DC.

View SolutionIn the figure, ¯¯¯¯¯¯AB || ¯¯¯¯¯¯CDand¯¯¯¯¯¯AD || ¯¯¯¯¯¯BC. If ∠ABC=110∘,∠ACD=30∘, then find ∠ADC.

View SolutionIn the adjoining figure, AB||CD. If the ∠BAE=25∘and∠CDE=30∘, then find ∠AED
View Solution