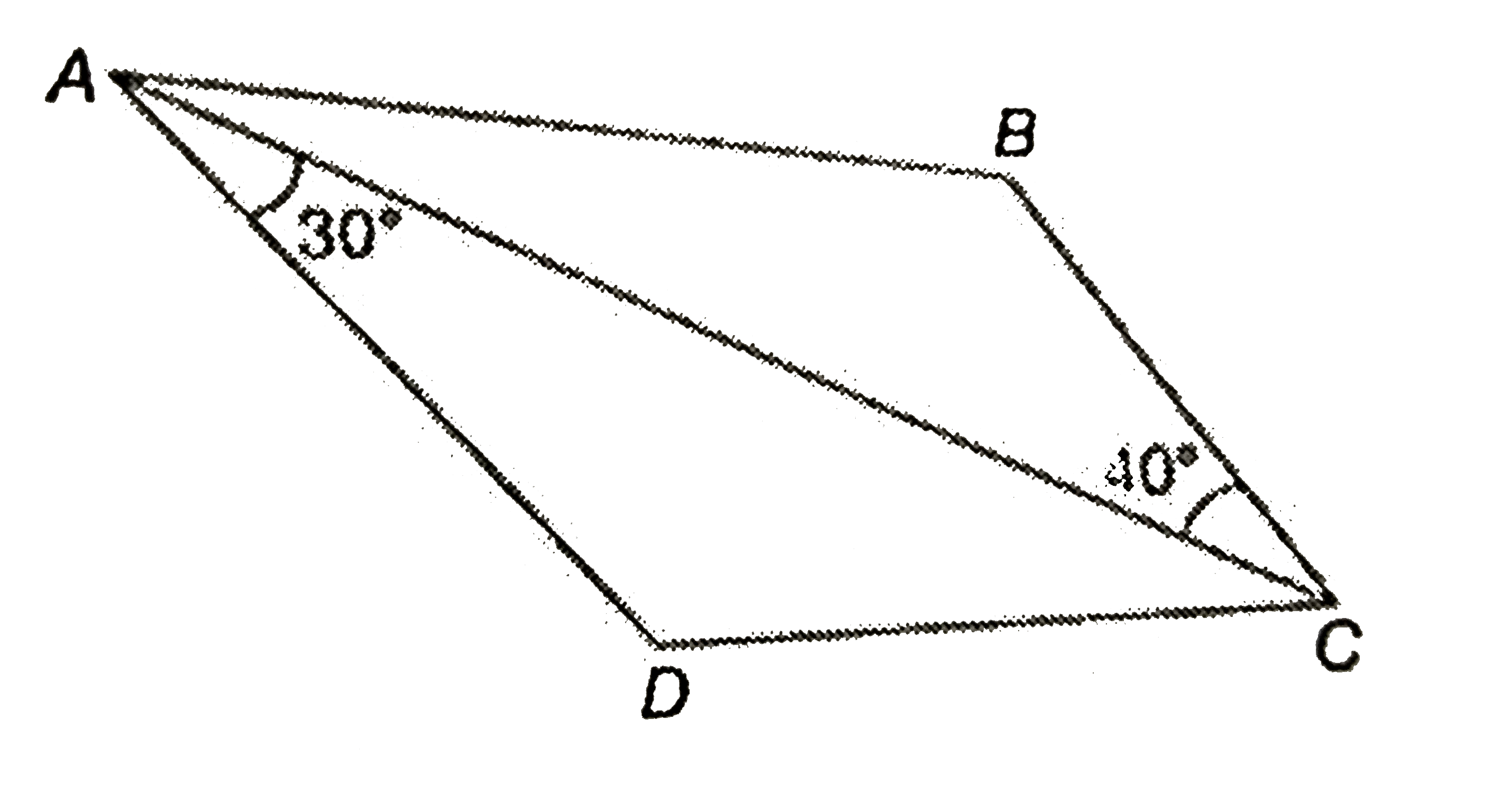
In the figure, ¯¯¯¯¯¯DC || ¯¯¯¯¯¯AB. If ∠ACB=40∘ and ∠CAD=30∘, AC is the bisector of ∠DAB, then find the angle of ∠ADC.
Video Solution
Text Solution
The correct Answer is:120∘
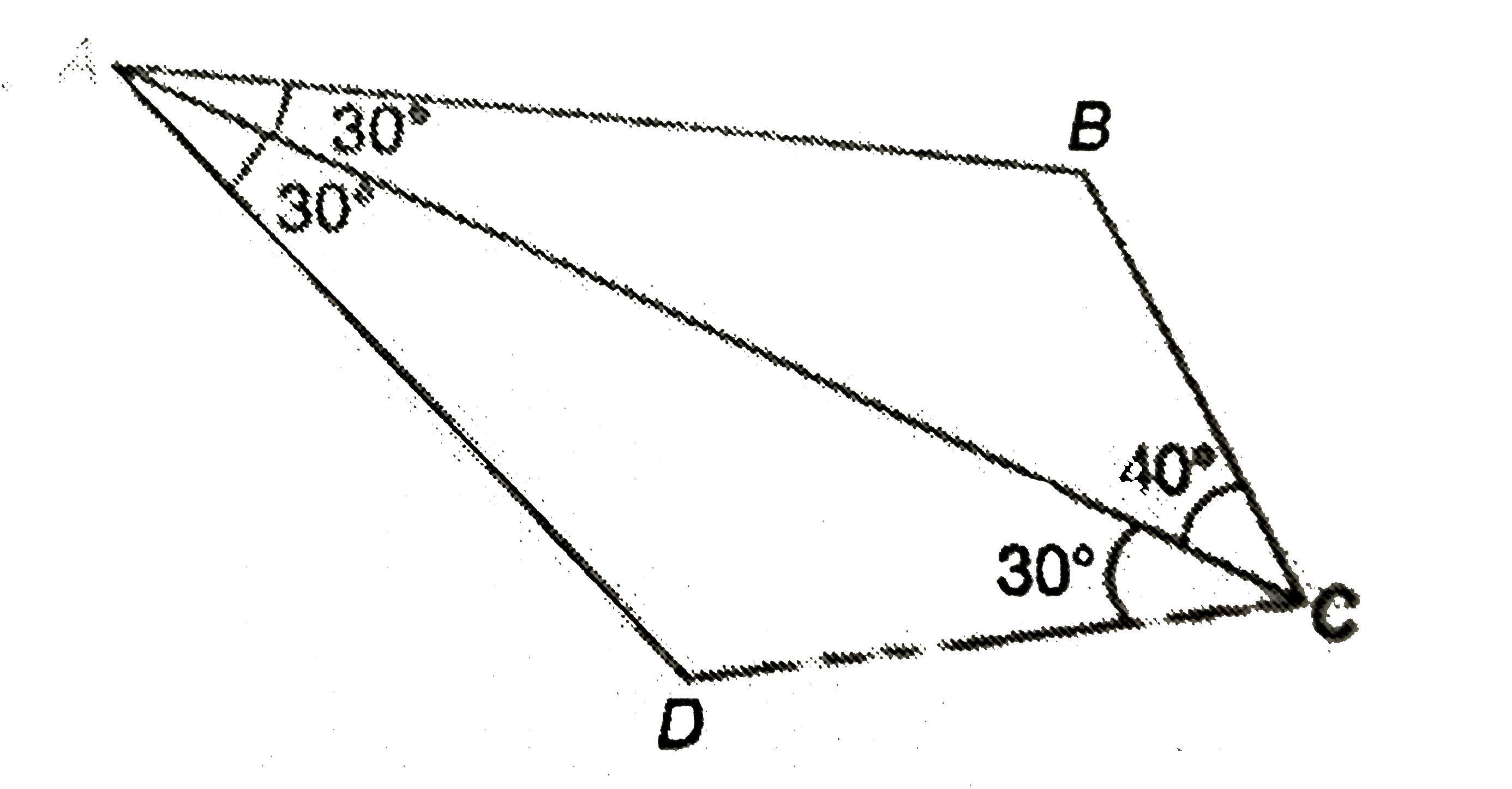
Given ∠CAD=30∘,∠ACB=40∘
As AC is the bisector of ∠BAD,∠CAD=∠BAC=30∘.
Given, ¯¯¯¯¯¯AB || ¯¯¯¯¯¯DC.
∴∠ACD=∠BAC=30∘
In ΔADC,∠ADC=180∘−30∘−30∘=120∘
|
Topper's Solved these Questions
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:CONCEPT APPLICATION
Explore 5 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:ASSESSMENT TEST
Explore 15 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 48 Videos
- FRACTIONS AND DECIMALS Book:PEARSON IIT JEE FOUNDATIONChapter:FRACTIONS AND DECIMALS Exercise:Crossword
Explore 1 Video
- MENUSRATION Book:PEARSON IIT JEE FOUNDATIONChapter:MENUSRATION Exercise:Crossword
Explore 1 Video
Similar Questions
Knowledge Check
In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD,∠BAE=30∘ and ∠CDE=35∘. If ¯¯¯¯¯¯AB⊥¯¯¯¯¯¯BC, then find ∠AED.A60∘B55∘C65∘D85∘In the following figure ∠B=70∘ and ∠C=30∘.BOandCO are the angle bisectors of ∠ABCand∠ACB. Find the value of ∠BOC:
 A30∘B40∘C120∘D130∘
A30∘B40∘C120∘D130∘
In the figure above, ¯¯¯¯¯¯AB||¯¯¯¯¯¯CD. Find the value of x.A50∘B45∘C60∘D40∘
In the following figure (not to scale), ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD. If ∠BAE=25∘ and ∠DCE=30∘, then find ∠AEC.
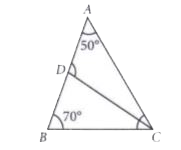
View SolutionIn △ABC,∠A=50∘,∠B=70∘ and bisector of ∠C meets AB in D (see figure). Find the measure of ∠ADC.
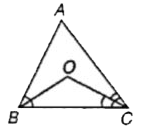
View SolutionIn figure, ∠ACB=40∘. Find ∠OAB.

View Solution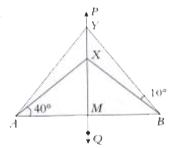
In the figure above ,¯¯¯¯¯¯PQ is the perpendicular bisector of ¯¯¯¯¯¯AB . If ∠XAB=40∘and∠XBY=10∘, then find ∠AYX
View Solution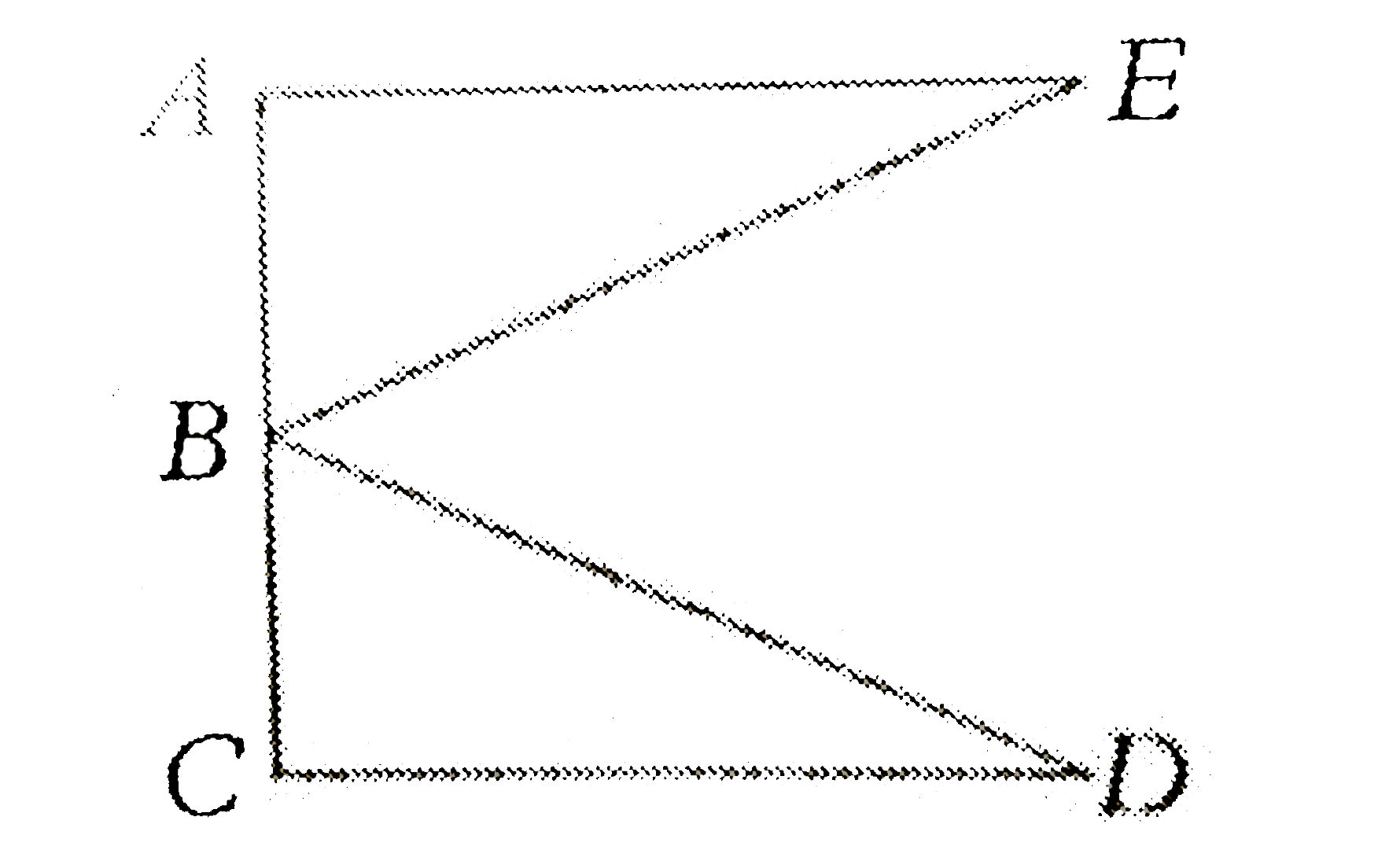
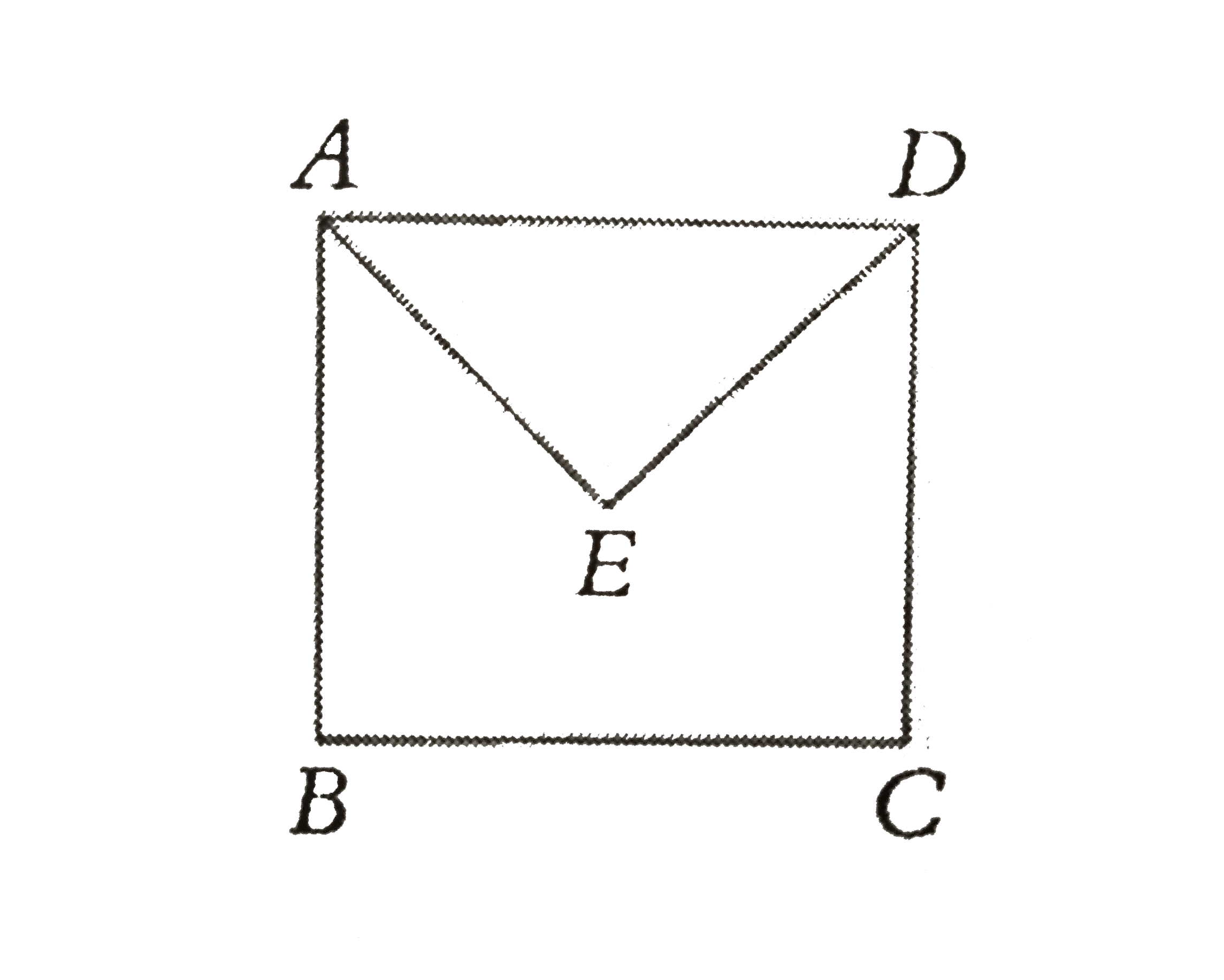
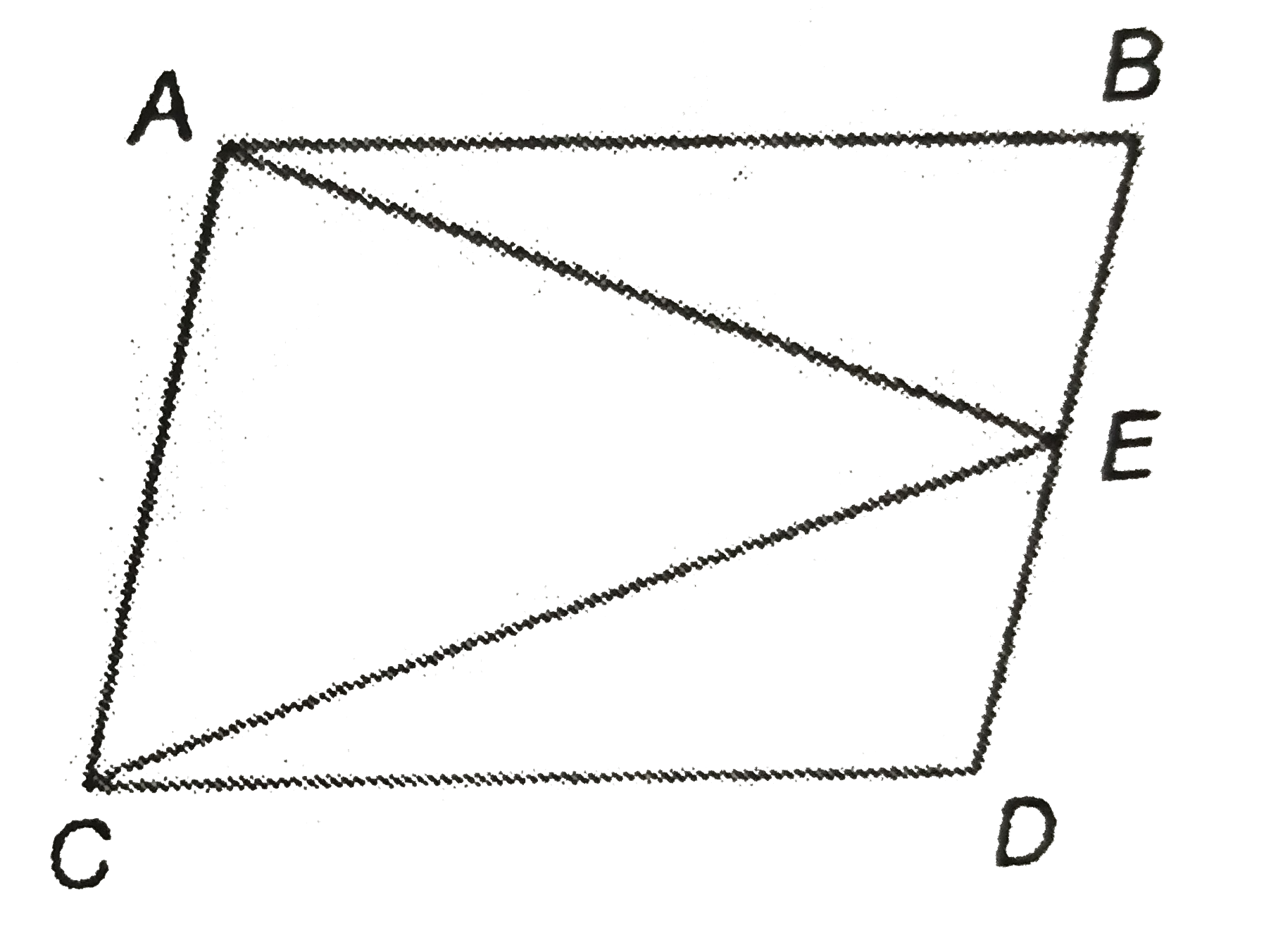
In the given figure, ¯¯¯¯¯¯AE∣∣¯¯¯¯¯¯CD, AB=BC, and AE=CD. If ¯¯¯¯¯¯AC⊥¯¯¯¯¯¯CDand∠AEB=35∘, then find ∠DBE.
View Solution

