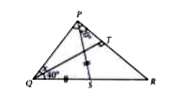
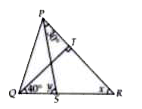
In the figure, PS and QT are two straight lines intersecting at the point R. PR = RQ. If ∠PRQ=98∘and∠TSR=40∘, then find the angles of ∠Tand∠Q.

The correct Answer is:42∘,41∘
∠TRS=∠PRQ=98∘ (vertically opposite angles)
In ΔTRS,
∠RTS=180∘−98∘−40∘
=180∘−138∘
=42∘
In ΔPQR,∠RPQ=∠RQP (sincePR=QR)
=(180∘−98∘)=82∘4=41∘
Topper's Solved these Questions
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:CONCEPT APPLICATION
Explore 5 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:ASSESSMENT TEST
Explore 15 Videos
- GEOMETRYBook:PEARSON IIT JEE FOUNDATIONChapter:GEOMETRYExercise:VERY SHORT ANSWER TYPE QUESTIONS
Explore 48 Videos
- FRACTIONS AND DECIMALS Book:PEARSON IIT JEE FOUNDATIONChapter:FRACTIONS AND DECIMALS Exercise:Crossword
Explore 1 Video
- MENUSRATION Book:PEARSON IIT JEE FOUNDATIONChapter:MENUSRATION Exercise:Crossword
Explore 1 Video
Similar Questions
Knowledge Check
In the given figure, PQRS is a quadrilateral ,PR and QS intersect at O. If ∠PQR=70∘,∠SPQ=80∘,and∠PRQ=60∘, then find ∠SPR.A30∘B50∘C40∘D45∘In figure, if QT⊥PR,∠TQR=40∘and∠SPR=30∘, find value of y-x
 A80∘B50∘C30∘D130∘
A80∘B50∘C30∘D130∘In the given figure, two straight lines AB and CD intersect at a point and ∠AOC = 50∘. Then, ∠BOD = ?
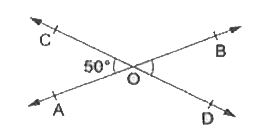 A40∘B50∘C130∘D60∘
A40∘B50∘C130∘D60∘
In the given figure, three lines AB, CD and EF intersect at a point O such that ∠AOE=35∘ and ∠BOD=40∘. Find the measure of ∠AOC,∠BOF,∠COF and ∠DOE.
View SolutionIn the given figure, name:
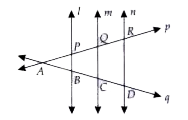
lines whose point of intersection is R
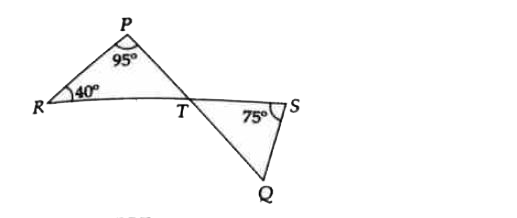
View SolutionIn the given figure lines PQ and RS intersect at point T such that ∠PRT=40∘∠RPT=95∘ and ∠TSQ=75∘ find ∠SQT
View SolutionIn the given figure,two straight line AB and CD intersect at a point O.
If ∠AOC=42∘,Find the measure of each of the angles:
∠AOD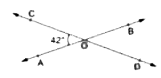
If ∠AOC=42∘,Find the measure of each of the angles:
∠BOD
If ∠AOC=42∘,Find the measure of each of the angles:
an≤COB
View SolutionTwo lines AB and CD intersect at a point O.∠AOC=40∘,find the measure of each of the angles ∠AOD,∠BODand∠BOC.
View Solution