
From a uniform square plate of side a and mass , a square portion DEFG of side is removed. Then, the moment of inertia of remaining portion about the axis AB is
The correct Answer is:B
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct36videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 21videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective32videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Four spheres of diameter a and mass m each are arranged at the corners of a square of side 1. Calculate the moment of inertia of the system about CD taken as its axis.
View SolutionFrom a ring of mass M and radius R, a 30o sector is removed. The moment of inertia of the remaining portion of the ring, about an axis passing through the centre and perpendicular to the plane of the ring is
View Solution
Knowledge Check
- Question 1 - Select One
Four holes of radius R are cut from a thin square plate of side 4R and mass M. The moment of inertia of the remaining portion about z-axis is :
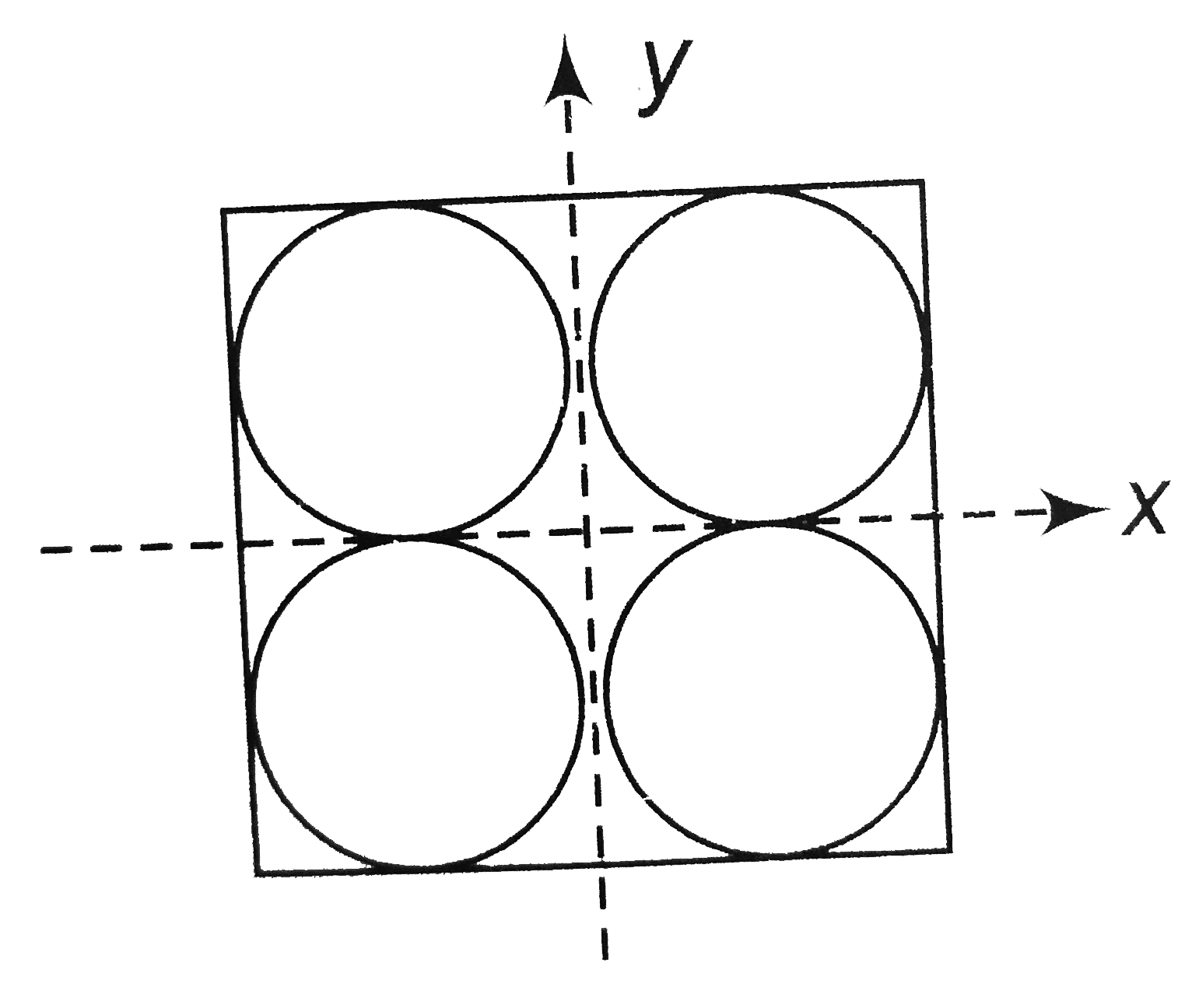 .Aπ12MR2B(43−π4)MR2C(83−10π16)MR2D(43−π6)MR2.
.Aπ12MR2B(43−π4)MR2C(83−10π16)MR2D(43−π6)MR2. - Question 2 - Select One
A square plate of edge a/2 is cut out from a uniform square plate of edge 'a' shown in figure. The mass of the remaining portion is M. The moment of inertia of the shaded portion about an axis passing through 'O'( centre of the square of side a) and perpendicular to plane of the plate is :
 A964Ma2B316Ma2C512Ma2DMa26
A964Ma2B316Ma2C512Ma2DMa26 - Question 3 - Select One
In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
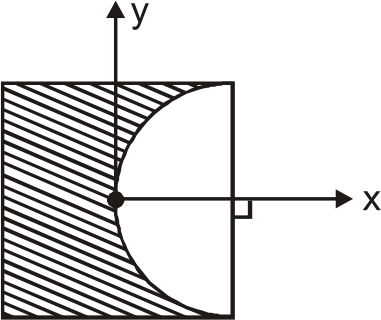 A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
There are four solid balls with their centres at the four comers of a square of side a. the mass of each sphere is m and radius is r. Find the moment of inertia of the system about (i) one of the sides of the square (ii) one of the diagonals of the square.
View SolutionA square of side a2 is removed from a disc having radius a . Find centre of mass of remaing portion.
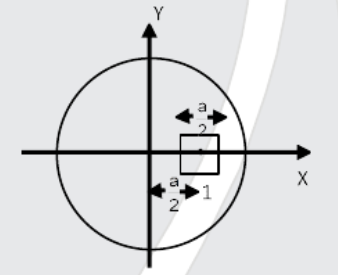 View Solution
View SolutionA square plate of side / has mass M. What is its moment of inertia about one of its diagonals ?
View SolutionFour thin uniform rods each of length L and mass m are joined to form a square . The moment of inertia of square about an axis along its one diagonal is
View SolutionFour spheres each having mass m and radius r are placed with their centres on the four comers of a square of side a. Then the moment of inertia of the system about an axis along one of the sides of the square, is
View Solution


