Four thin uniform rods each of length L and mass m are joined to form a square . The moment of inertia of square about an axis along its one diagonal is
mL26
23mL2
3mL24
4mL23
The correct Answer is:B
To find the moment of inertia of a square frame made of four uniform rods about an axis along one of its diagonals, we can follow these steps:
Step 1: Understand the Configuration
We have a square frame formed by four thin uniform rods, each of length L and mass m. The square has its diagonals, and we need to find the moment of inertia about one of these diagonals.
Step 2: Moment of Inertia of a Single Rod
The moment of inertia I of a single rod about an axis passing through its center and perpendicular to its length is given by the formula:
Irod=112mL2
Step 3: Moment of Inertia of the Square Frame
Since the square frame consists of four rods, we can calculate the total moment of inertia about an axis through the center of the square (perpendicular to the plane of the square) by considering the contribution of each rod. However, we will first find the moment of inertia of one rod about the diagonal.
Step 4: Using the Parallel Axis Theorem
To find the moment of inertia of a rod about an axis that is not through its center, we can use the parallel axis theorem:
I=Icm+md2
where d is the distance from the center of mass of the rod to the new axis.
For a rod lying along one side of the square, the distance d to the diagonal is L2. Therefore, for one rod:
Idiagonal=112mL2+m(L2)2=112mL2+mL24=112mL2+312mL2=412mL2=13mL2
Step 5: Total Moment of Inertia for the Square Frame
Since there are four rods, the total moment of inertia about the diagonal is:
Itotal=4×13mL2=43mL2
Step 6: Using the Perpendicular Axis Theorem
The perpendicular axis theorem states that for a planar body:
Iz=Ix+Iy
where Iz is the moment of inertia about an axis perpendicular to the plane, and Ix and Iy are the moments of inertia about two perpendicular axes in the plane.
Since the square is symmetric, we can say:
Ix=Iy
Thus, we have:
Iz=2Ix⟹Ix=Iz2
Substituting Iz=43mL2:
Ix=43⋅12mL2=23mL2
Final Answer
The moment of inertia of the square about one of its diagonals is:
I=23mL2
We have a square frame formed by four thin uniform rods, each of length L and mass m. The square has its diagonals, and we need to find the moment of inertia about one of these diagonals.
The moment of inertia I of a single rod about an axis passing through its center and perpendicular to its length is given by the formula:
Irod=112mL2
Since the square frame consists of four rods, we can calculate the total moment of inertia about an axis through the center of the square (perpendicular to the plane of the square) by considering the contribution of each rod. However, we will first find the moment of inertia of one rod about the diagonal.
To find the moment of inertia of a rod about an axis that is not through its center, we can use the parallel axis theorem:
I=Icm+md2
where d is the distance from the center of mass of the rod to the new axis.
Idiagonal=112mL2+m(L2)2=112mL2+mL24=112mL2+312mL2=412mL2=13mL2
Since there are four rods, the total moment of inertia about the diagonal is:
Itotal=4×13mL2=43mL2
The perpendicular axis theorem states that for a planar body:
Iz=Ix+Iy
where Iz is the moment of inertia about an axis perpendicular to the plane, and Ix and Iy are the moments of inertia about two perpendicular axes in the plane.
Ix=Iy
Thus, we have:
Iz=2Ix⟹Ix=Iz2
Substituting Iz=43mL2:
Ix=43⋅12mL2=23mL2
The moment of inertia of the square about one of its diagonals is:
I=23mL2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - III
Explore 43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (C.W)
Explore 60 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
four thin rods each of mass m and length l are joined to make a square. Find moment of inertia of all the four rods about any side of the square.
View SolutionA thin uniform wire of mass m and length l is bent into to shape of a semicircle. The moment of inertia of that wire about an axis passing through its free ends is
View Solution
Knowledge Check
A thin wire of length l and mass m is turned into the form of a semicircle. Its moment of inertia about an axis joining its free ends will be
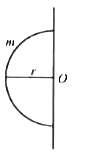 Amπl2Bml2/π2Cml22πDml22π2
Amπl2Bml2/π2Cml22πDml22π2Three identical thin rods each of length l and mass M are joined together to form a letter H. What is the moment of inertia of the system about one of the sides of H?
A16Ml2B14Ml2C23Ml2D43Ml2A rigid body is made of three identical thin rods, each of length L fastened together in the form of the letter H. The moment of inertia of this body about an axis that runs along the length of one of the legs of H is
AML23B4ML23CML2D3ML2
Three identical thin rods each of length l and mass M are joined together to from a letter. H. What is the moment of inertia of the system about one of the sides of H ?
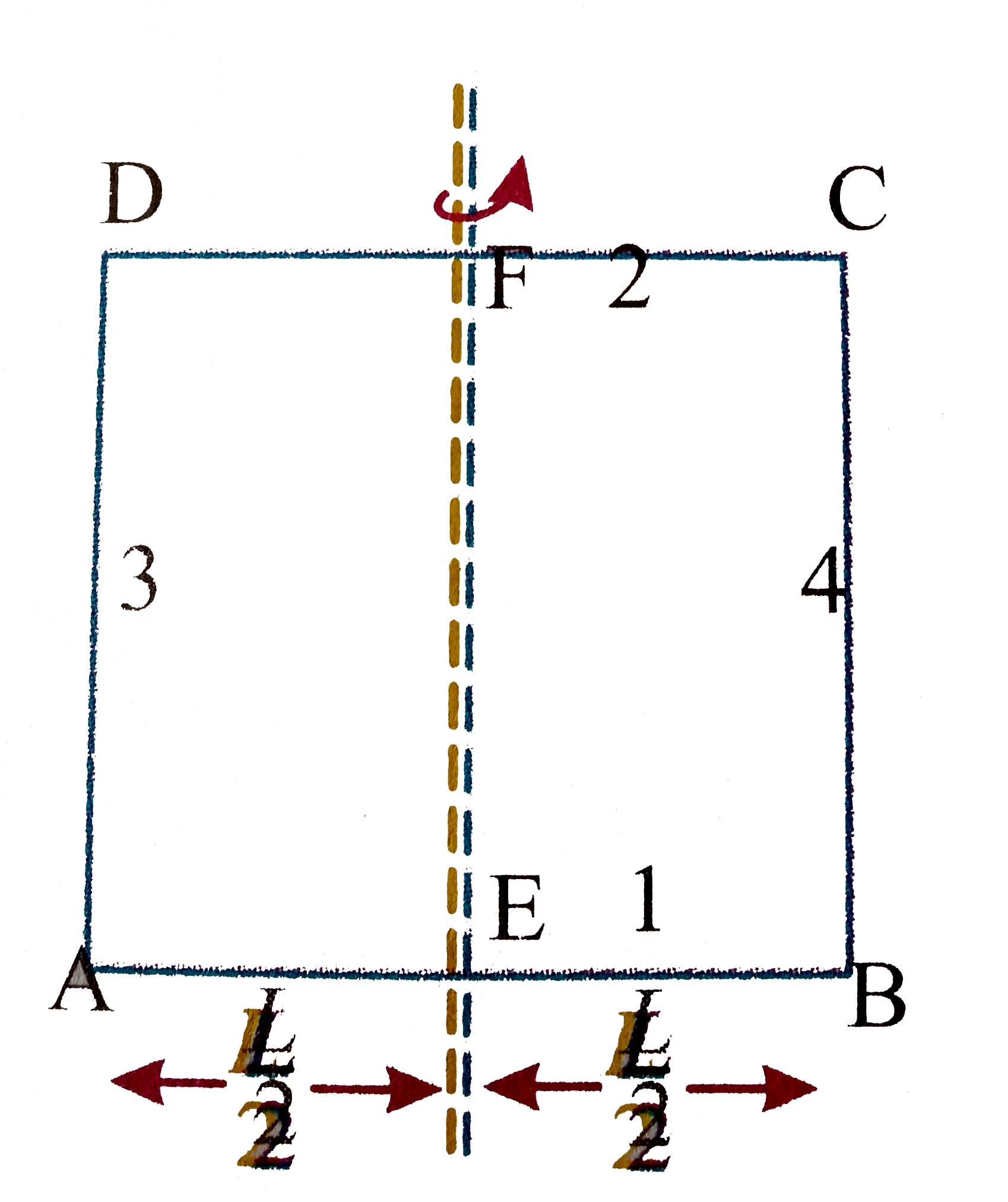
View SolutionFour thin metal rods, each of mass M and length L, are welded to form a square ABCD as shown in figure. The moment of inertia of composite structure about a line which bisects rods AB and CD is
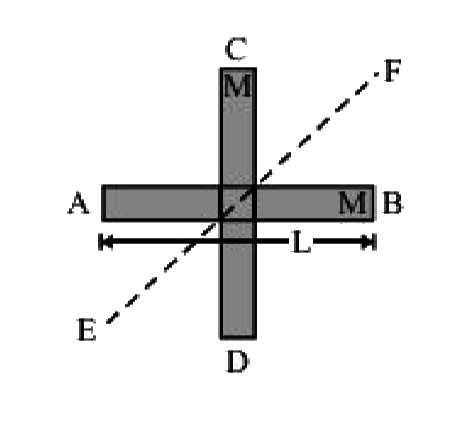
View SolutionTwo uniform thin identical rods AB and CD each of mass M and length L are joined so as to form a cross as shown. The moment of inertia of the cross about a bisector line EF is :-
View SolutionThree indentical thin rods each of mass m and length L are joined together to form an equilateral triangular frame . The moment of inertia of frame about an axis perpendicular to the palne of frame and apssing through a corner is
View SolutionTwo uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View Solution

