Three indentical thin rods each of mass m and length L are joined together to form an equilateral triangular frame . The moment of inertia of frame about an axis perpendicular to the palne of frame and apssing through a corner is
2mL23
3mL22
4mL23
3mL24
The correct Answer is:B
To find the moment of inertia of the equilateral triangular frame made of three identical thin rods about an axis perpendicular to the plane of the frame and passing through one of its corners, we can follow these steps:
Step 1: Identify the rods and their arrangement
We have three identical rods, each of mass m and length L, arranged to form an equilateral triangle. Let's label the rods as R1, R2, and R3.
Step 2: Calculate the moment of inertia of each rod about the axis
1. Rod R1: This rod is aligned along one side of the triangle and passes through the axis. The moment of inertia of a rod about an axis through one end perpendicular to its length is given by:
I1=13mL2
2. Rod R2: This rod is also aligned along one side of the triangle but does not pass through the axis. We need to use the parallel axis theorem to find its moment of inertia about the given axis. The moment of inertia about its center of mass is:
Icm=13mL2
The distance from the center of mass of rod R2 to the axis is d=L√32 (since it is at a 30∘ angle). Therefore, using the parallel axis theorem:
I2=Icm+md2=13mL2+m(L√32)2
I2=13mL2+m3L24=13mL2+34mL2
To combine these, we need a common denominator:
I2=412mL2+912mL2=1312mL2
3. Rod R3: This rod is similar to rod R2 and will have the same moment of inertia about the axis:
I3=I2=1312mL2
Step 3: Sum the moments of inertia
Now, we can find the total moment of inertia I of the triangular frame about the given axis:
I=I1+I2+I3
Substituting the values we calculated:
I=13mL2+1312mL2+1312mL2
I=13mL2+2612mL2
To combine these, we convert 13 to a fraction with a denominator of 12:
13=412
So,
I=412mL2+2612mL2=3012mL2=52mL2
Final Result
Thus, the moment of inertia of the triangular frame about the specified axis is:
I=52mL2
We have three identical rods, each of mass m and length L, arranged to form an equilateral triangle. Let's label the rods as R1, R2, and R3.
1. Rod R1: This rod is aligned along one side of the triangle and passes through the axis. The moment of inertia of a rod about an axis through one end perpendicular to its length is given by:
I1=13mL2
Icm=13mL2
The distance from the center of mass of rod R2 to the axis is d=L√32 (since it is at a 30∘ angle). Therefore, using the parallel axis theorem:
I2=Icm+md2=13mL2+m(L√32)2
I2=13mL2+m3L24=13mL2+34mL2
To combine these, we need a common denominator:
I2=412mL2+912mL2=1312mL2
I3=I2=1312mL2
Now, we can find the total moment of inertia I of the triangular frame about the given axis:
I=I1+I2+I3
Substituting the values we calculated:
I=13mL2+1312mL2+1312mL2
I=13mL2+2612mL2
To combine these, we convert 13 to a fraction with a denominator of 12:
13=412
So,
I=412mL2+2612mL2=3012mL2=52mL2
Thus, the moment of inertia of the triangular frame about the specified axis is:
I=52mL2
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - II (H.W)
Explore 60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - III
Explore 43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - I(H.W)
Explore 63 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-VI
Explore 78 Videos
- THERMAL PROPERTIES OF MATTERBook:NARAYNAChapter:THERMAL PROPERTIES OF MATTERExercise:LEVEL - II (H.W.)
Explore 19 Videos
Similar Questions
Three identical thin rods, each of mass m and length l, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to tis one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.
View Solution
Knowledge Check
In the above problem the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
AML2B2ML2C2√2ML2D4ML2In the above problem the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
AML2B2ML2C2√2ML2D4ML2A rod of mass Mkg and length Lm is bent in the from of an equilateral tringle as shown in Gig. The moment of inertia of the triangle about a vertical axis perpendicular to the plane of the triangle and passing through the centre (in units of kgm2) is.
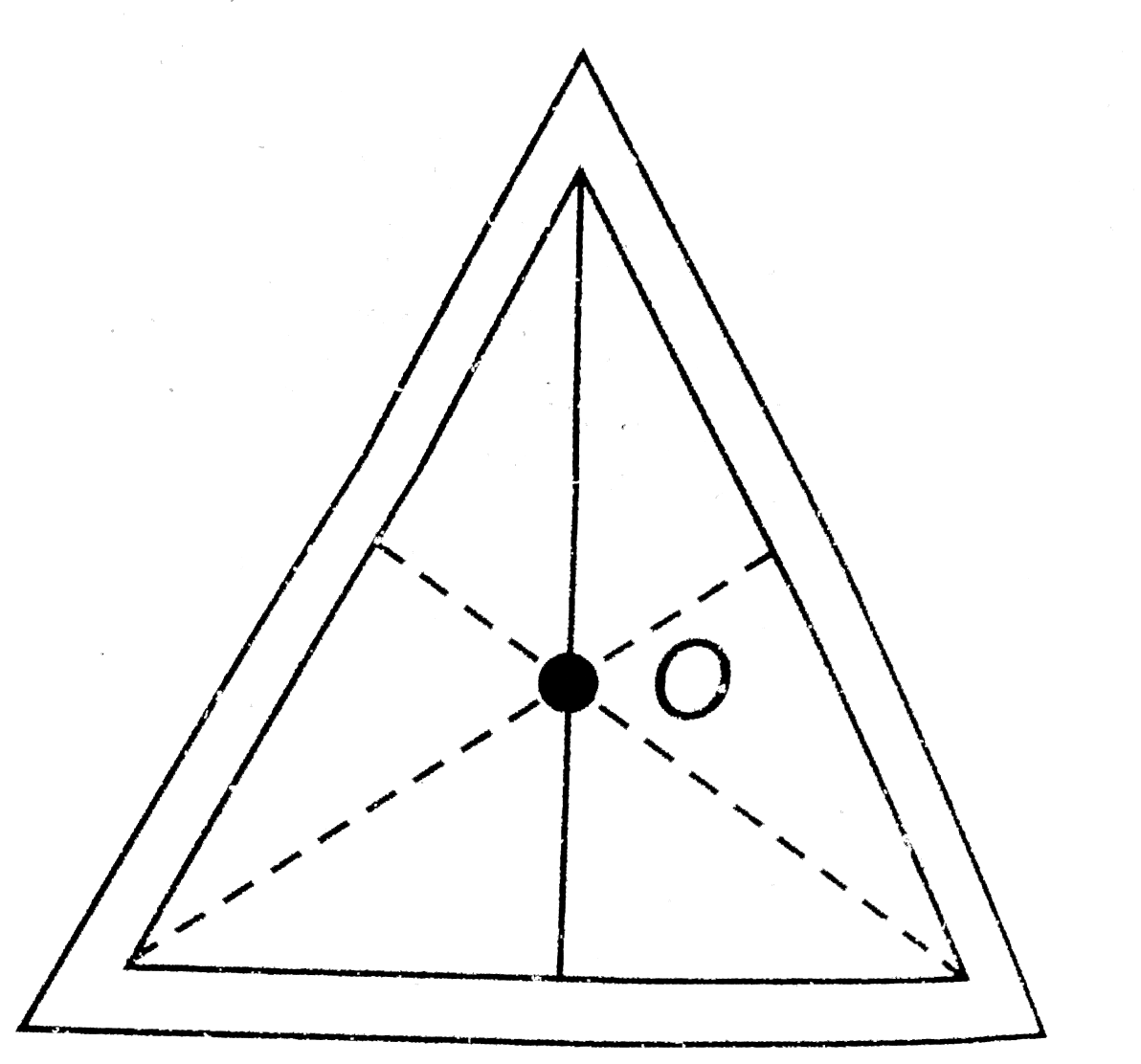 .AML212BML254CML2162DML2108
.AML212BML254CML2162DML2108
Three identical thin rods each of length l and mass M are joined together to form a letter H. What is the moment of inertia of the system about one of the sides of H?
View SolutionThree identical thin rods each of length l and mass M are joined together to from a letter H. What is the moment of inertia of the system about one of the sides of H ?
View SolutionFour particles each of mass m are placed at the corners of a square of side length l. The radius of gyration of the system the moment of inertia of four bodies about an axis perpendicular to the plane of frame and passing through a corner is
View SolutionFour point size bodies each of mass M are fixed at four corners of a light square frame of side length L. The moment of inertia of the four bodies about an axis perpendicular to the plane of frame and passing through its centre is
View SolutionThree identical thin rods each of length l and mass M are joined together to from a letter. H. What is the moment of inertia of the system about one of the sides of H ?
View Solution

