I is moment of inertia of a thin circular plate about its natural axis. The moment of inertia of a circular ring whose mass is half of mass of plate but radius is twice the radius of plate about an axis passing through any tangent of ring in its plane is
3I
4I
6I
1.5I
The correct Answer is:C
,I1=32M1R21=32[M2][2R]2=6I
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - II (H.W)
60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - III
43 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - NARAYNACHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - EXERCISE - I(H.W)
63 Videos
- SYSTEM OF PARTICLESBOOK - NARAYNACHAPTER - SYSTEM OF PARTICLESEXERCISE - Level-VI
78 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NARAYNACHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - LEVEL - II (H.W.)
19 Videos
Similar Questions
Knowledge Check
A moment of inertia of a thin circular plate is minimum about the following axis
Aaxis perpendicular to plane of plate passing through its centreBaxis passing through any diameter of plateCaxis passing through any tangent of plate in its planeDaxis passing through any tangent perpendicular to its planeIf I moment of inertia of a thin circular plate about an axis passing through tangent of plate in its plane. The moment of inertia of same circular plate about an axis perpendicular to its plane and passing through its centre is
A4I5B2I5C4I3D2I3Moment of inertia of a thin circular plate of mass M, radius R about an axis passing through its diameter is I. The moment of inertia of a circular ring of mass M, radius R about an axis perpendicular to its plane and passing through its centre is
A2IBI2C4IDI4
The moment of inertia of a ring of mass M and radius R about PQ axis will be :-
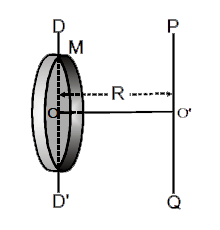
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
View SolutionI is moment of inertia of a thin square plate about an axis passing through opposite corners of plate. The moment of inertia of same plate about an axis perpendicular to the plane of plate and passing through its centre is
View SolutionThe moment of inertia of a circular plate of unit diameter and of unit mass about its diameter is,
View SolutionThe moment of inertia of ring about an axis passing through its diameter is I. Then moment of inertia of that ring about an axis passing through its centre and perpendicular to its plane is
View Solution

