
A small solid sphere of mass m and radius r starting from rest from the rim of a fixed hemispherical bowl of radius R(>>r) rolls inside it without sliding. The normal reaction exerted by the sphere on the hemisphere when it reaches the bottom of hemisphere is
(3/7)mg
(9/7)mg
(13/7)mg
(17/7)mg
At bottom total kinetic energy
= decrease in potential energy
=mgR
The ratio KRKT=25
∴KT=12mv2=57mgR
∴mv2R=107mg=N−mg
∴N=177mg

Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Multiple Correct
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A solid uniform sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls without sliding along the surface. If the rim of the hemisphere is kept horizotnal, find the normal force exerted by the cup on the ball when the ball reaches the bottom of the cup.
View SolutionConsider the situation as shown in the figure. A solid sphere of mass m is released from rest from the rim of a hemispherical cup so that it rolls along the surface. Find the normal contact force between the solid sphere and the cup at the bottom most point.
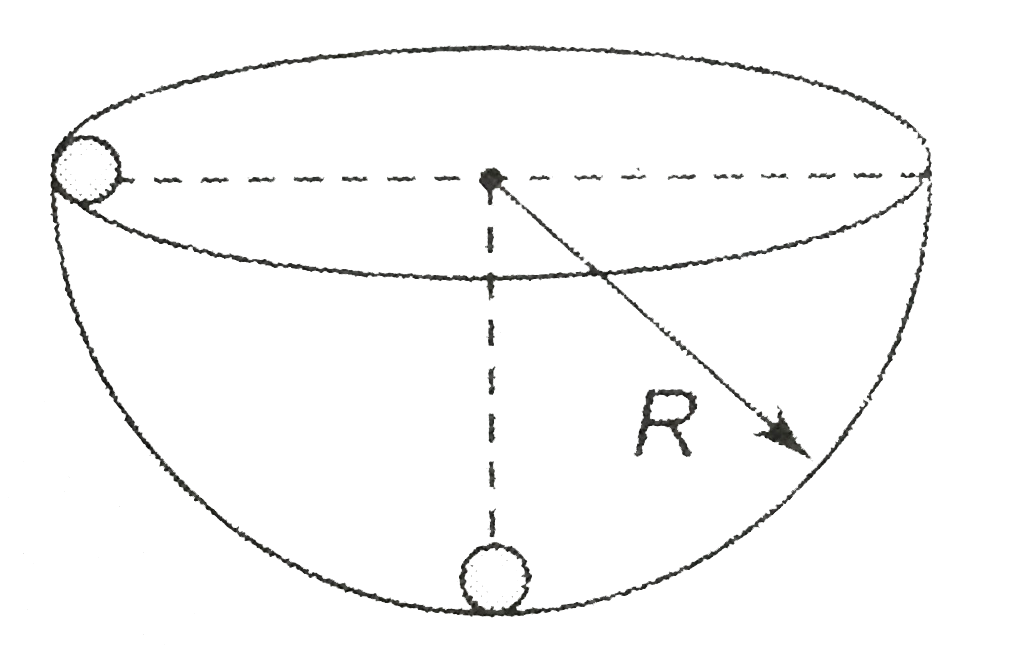
View Solution
Knowledge Check
A small sphere D of mass and radius rols without slipping inside a large fixed hemispherical radius R(>>r) as shown in figure. If the sphere starts from rest at the top point of the hemisphere normal force exerted by the small sphere on the hemisphere when its is at the bottom B of the hemisphere.
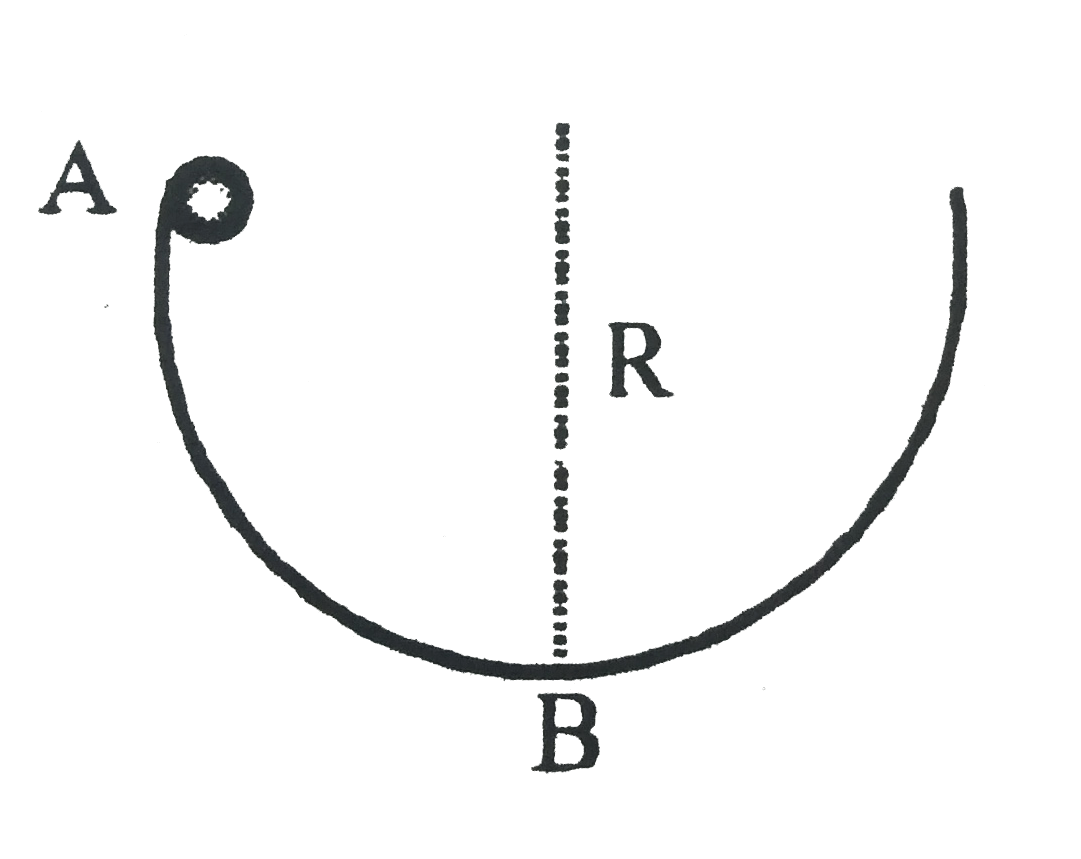 .A107mgB177mgC57mgD75mg
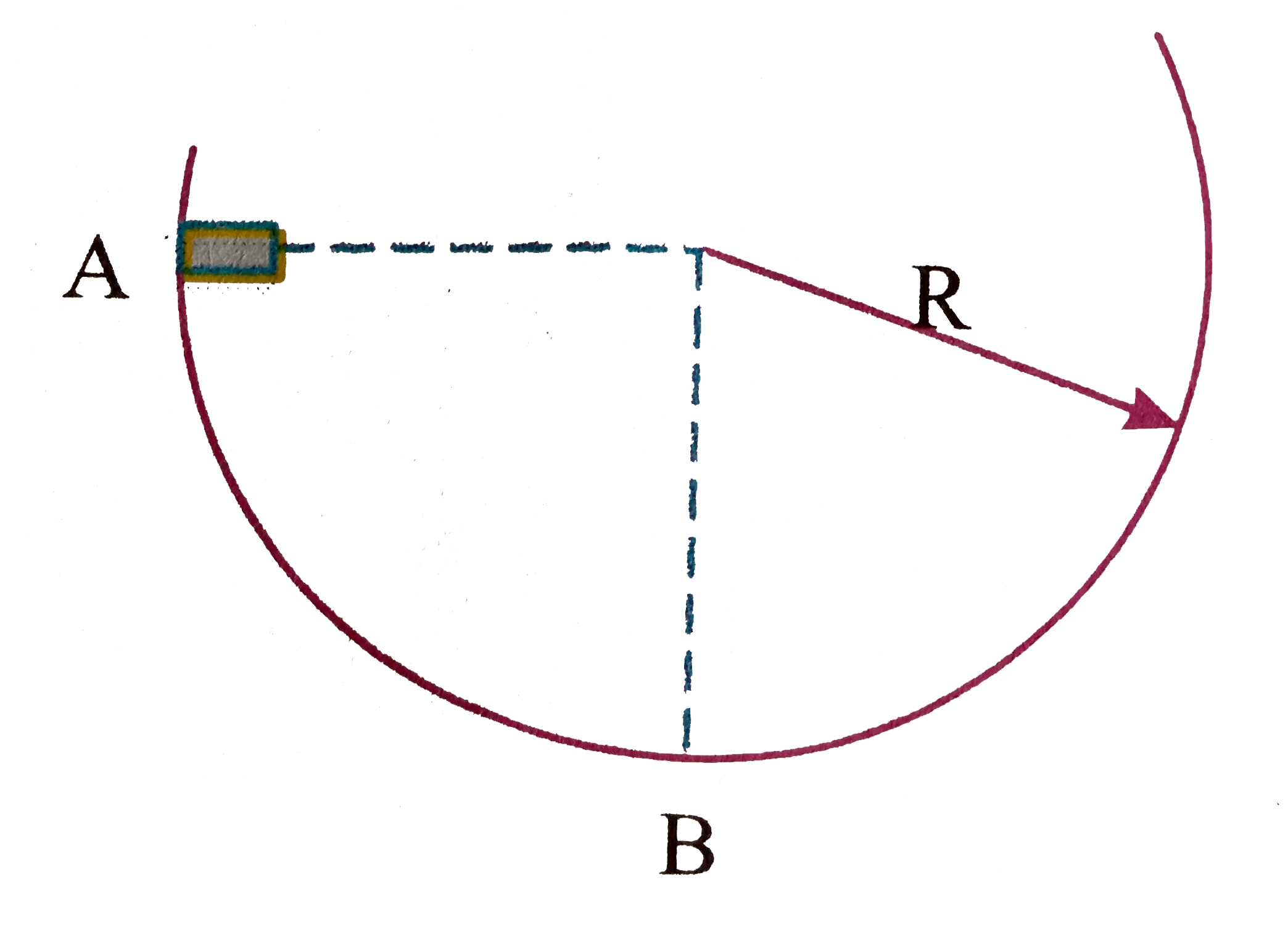
.A107mgB177mgC57mgD75mgA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.
 AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at B
AAcceleration of block is constant throughoutBAcceleration of block is g at ACAcceleration of block is 3g at BDAcceleration of block is 2g at BThe distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3
A small steel sphere of mass m and radius r rolls without slipping on the fiictionless surface of a large hemisphere of radius R{R gt gt r) whose axis of symmetry is vertical. It starts at the top from the rest, (a) What is the kinetic energy at the bottom ? (b) What fraction is the rotational kinetic energy of the total kinetic energy at the bottom? (b) What fraction is the rotational kinetic energy of the total kinetic energy? (c) What fraction is the translational kinetic energy of the total kinetic energy? (d) Calculate the normal force that the small sphere will exerton.the hemisphere at its bottom. Howthe results will be affected if r is not very sjnall as compared to R.
View SolutionA small block of mass m starts sliding down from rest along the smooth surface of a fixed hollow hemisphere of same mass m. Find the distance of centre of mass of block and hemishere from centre of hemisphere C when block m separates from the surface of hemisphere.
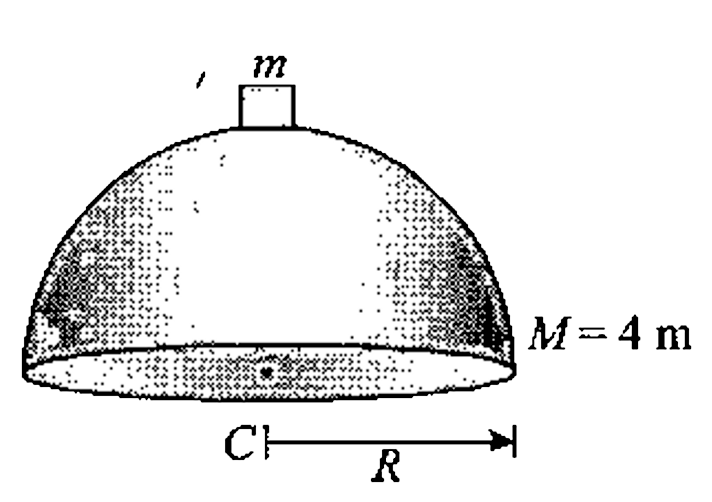
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View SolutionA particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .
.
View Solution
