Complete Solutions to MCQs of chapter OSCILLATIONS of Class 11 book with complete answers and questions
| Class 11 | PHYSICS |
| Chapter | OSCILLATIONS |
| NCERT FINGERTIPS | MCQs |
| Number Of Questions | 86 |
| Academic Year | 2023-24 |
All trignometric functions are periodic but only sine or cosine functions are used to define SHM. Why?
View SolutionThe Halley's comet appears after every
View SolutionWhich one of the following is not a periodic motion?
View SolutionWhich of the following x-t graphs does not represent periodic motion?
View SolutionIf the frequency of human heart is 1.25 Hz, the number of heart beats in 1 minutes is
View SolutionIn a certain oscillatory system (particle is performing SHM), the amplitude of motion is 5 m and the time period is 4 s. the minimum time taken by the particle for passing betweens points, which are at distances of 4 m and 3 m from the centre and on the same side of it will approximately be
View SolutionA body of mass m is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand so that the spring is neither stretched nor compressed. Suddenly the support of the hand is removed. The lowest position attained by the mass during oscillation is 4cm below the point, where it was held in hand.
(a) What is the amplitude of oscillation ?
(b) Find the frequency of oscillation?
View SolutionOut of the following functions representing motion of a particle which represents SHM?
1. `x=sin^(3)omegat`
2. `x=1+omegat+omega^(2)t^(2)`
3. `x=cosomegat+cos3omegat+cos5omegat`
4. `x=sinomegat+cosomegat`
View SolutionWhich of the following is not characteristics of simple harmonic motion?
View SolutionThe equation of motion of a simple harmonic motion is
View SolutionWhich of the following expression does not represent simple harmonic motion?
View SolutionIf a simple harmonic motion is represented by `(d^(2)x)/(dt^(2)) + alphax = 0`, its time period is :
View SolutionThe time period of simple harmonic motion depends upon
View SolutionWhich of the following motions is not simple harmonic?
View SolutionIf x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
View SolutionWhich of the following functions of time represent (a) simple harmonic motion and (b) periodic but not simple harmonic motion? Give the period for each case.
(i)` sinomegat-cosomegat` (ii) `sin^(2)omegat` (iii) `cosomegat+2sin^(2)omegat`
View SolutionA particle executing simple harmonic motion with an amplitude A. The distance travelled by the particle in one time period is
View SolutionTwo simple harmonic motions are represented by the equations.
`y_(1)=10"sin"(pi)/(4)(12t+1),y_(2)=5(sin3pt+sqrt(3)cos3pt)` the ratio of their amplitudes is
View SolutionFigure shows the displacement-time graphs of two simple harmonic motions I and II. From the graph it follows that

View SolutionA vibratory motion is represented by `x=2Acosomegat+Acos(omegat+(pi)/(2))+Acos(omegat+pi)+(A)/(2)cos(omegat+(3pi)/(2))`.
the resultant amplitude of the motion is
View SolutionA particle executing SHM is described by the displacement function `x(t)=Acos(omegat+phi)`, if the initial (t=0) position of the particle is 1 cm, its initial velocity is `pi" cm "s^(-1)` and its angular frequency is `pis^(-1)`, then the amplitude of its motion is
View SolutionTwo particles execute SHMs of the same amplitude and frequency along the same straight line. They cross one another when going in opposite direction. What is the phase difference between them when their displacements are half of their amplitudes ?
View SolutionTwo particles execute SHM of same amplitude and frequency on parallel lines. They pass one another when moving in opposite directions each time their displacement is one third their amplitude. What is the phase difference between them?
View SolutionA mass of 2kg is attached to the spring of spring constant `50Nm^(-1)`. The block is pulled to a distance of 5 cm from its equilibrium position at `x=0` on a horizontal frictionless surface from rest at t=0. Write the expression for its displacement at anytime t.
View SolutionA non viscous liquid of density `rho` is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

View Solutionthe circular motion of a particle with constant speed is
View SolutionSimple harmonic motion is the projection of uniform circular motion on
View SolutionIn an SHM, x is the displacement and a is the acceleration at time t. the plot of a against x for one complete oscillation will be
View SolutionWhich one of the following statement is true for the speed `v` and the acceleration a of a particle executing simple harmonic motion?
View SolutionWhich of the following relationships between the acceleration a and the displacement x of a particle executing simple harmonic motion?
View SolutionA particle executing simple harmonic motion with an amplitude A and angularr frequency `omega`. The ratio of maximum acceleration to the maximum velocity of the particle is
View SolutionA particle executing SHM with time period T and amplitude A. The mean velocity of the particle averaged over quarter oscillation, is
View SolutionA particle executing SHM. The phase difference between velocity and displacement is
View SolutionA particle executing SHM. The phase difference between acceleration and displacement is
View SolutionA mass attached to a spring is free to oscillate, with angular velocity `omega`, in a horizontal plane without friction or damping. It is pulled to a distance `x_(0)` and pushed towards the centre with a velocity `v_(0)` at time `t=0`. Determine the amplitude of the resulting oscillations in terms of the parameters `omega, x_(0)and v_(0)`.
View SolutionThe piston in the cylinder head of a locomotive has a stroke (twice the amplitude) of 6.0m. If the piston moves with simple harmonic motion with an angular frequency of `200 (rad)/min`, what is its maximum speed ?
View SolutionA particle executing SHM according to the equation `x=5cos(2pit+(pi)/(4))` in SI units. The displacement and acceleration of the particle at t=1.5 s is
View SolutionA point mass oscillates along the x-axis according to the law `x=x_(0) cos(omegat-pi//4)`. If the acceleration of the particle is written as `a=Acos(omegat+delta)`, the .
View SolutionThe displacement of a particle executing simple harmonic motion is given by
`x=3sin(2pit+(pi)/(4))`
where x is in metres and t is in seconds. The amplitude and maximum speed of the particle is
View SolutionA particle executes SHM of period 12s. Two sec after it passes through the centre of oscillation, the velocity is found to be 3.142 cm `s^(-1)` find the amplitude and the length of the path.
View SolutionA particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
View SolutionA string of mass 3 kg is under tension of 400 N. the length of the stretched string is 25 cm. if the transverse jerk is stuck at one end of the string how long does the disturbance take to reach the other end?
View SolutionNatural length of a spring is 60 cm and its spring constant is 4000 N/m. A mass of 20 kg is hung from it. The extension produced in the spring is (Take, `g = 9.8 m//s^(2)`)
View SolutionIn simple harmonic motion, at the extreme positions
View SolutionThe total energy of a simple harmonic oscillation is proportional to
View SolutionA particle of mass m executing SHM with amplitude A and angular frequency `omega`. The average value of the kinetic energy and potential energy over a period is
View SolutionA simple harmonic oscillator has a period T and energy E. the amplitude of the oscillator is doubled. Choose the correct answer.
View SolutionA particle executing simple harmonic motion with time period T. the time period with which its kinetic energy oscillates is
View SolutionA particle executing SHM with an amplitude A. The displacement of the particle when its potential energy is half of its total energy is
View SolutionA particle of mass m is hanging vertically by an ideal spring of force constant K . If the mass is made to oscillate vertically, its total energy is
View SolutionFrequency of variation of kinetic energy of a simple harmonic motion of frequency n is
View SolutionWhen the displacement of a particle executing SHM is one-fourth of its amplitude, what fraction of the total energy is the kinetic energy?
View SolutionA block whose mass is 1 kg is fastened to a spring. The spring has a spring constant of 100N/m. the block is pulled to a distance x=10 cm from its equilibrium position at x=0 on a frictionless surface from rest at t=0. the kinetic energy and potential energy of the block when it is 5 cm away from the mean position is
View SolutionA body of mass m is situated in a potential field `U(x)=U_(0)(1-cosalphax)` when `U_(0)` and `alpha` are constant. Find the time period of small oscialltions.
View SolutionThe frequency of oscillations of a mass m suspended by spring of `v_(1)`. If the length of the spring is cut to one-half, the same mass oscillates with frequency `v_(2)`. Determine the value of `v_(2)//v_(1)`
View SolutionTime period of oscillation of a spring is 12 s on earth. What shall be the time period if it is taken to moon?
View SolutionA 5 kg collar is attached to a spring of spring constant 500 N `m^(-1)`. It slides without friction over a horizontal rod. The collar is displaced from its equilibrium position by 10 cm and released. The time period of oscillation is
View SolutionIn the question number 64, the maximum acceleration of the collar is
View SolutionA body of mass 20 g connected to a spring of spring constant k, executes simple harmonic motion with a frequency of `(5//pi)` Hz. The value of spring constant is
View SolutionAn air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
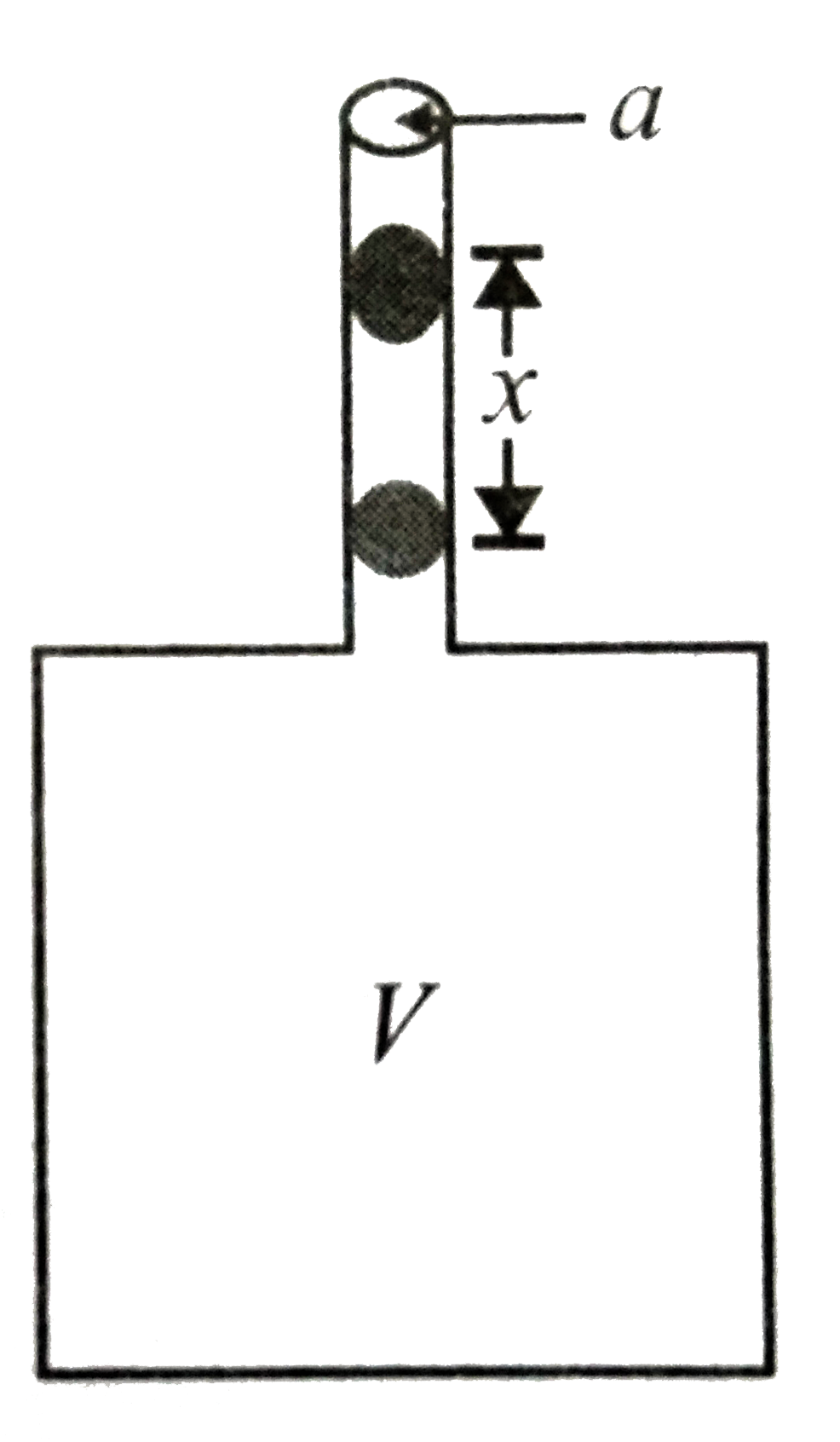
View SolutionA spring balance has a scale that reads from 0 to 50 kg. the length of the scale is 20 cm. a block of mass m is suspended from this balance, when displaced and released, it oscillates with a period 0.5 s. the value of m is (Take `g=10ms^(-2)`)
View SolutionTo show that a simple pendulum executes simple harmonic motion, it is necessary to assume that
View SolutionMotion of an oscillating liquid column in a U-tube is
View SolutionWhat is the effect on the time period of a simple pendulum if the mass off the bob is doubled?
View SolutionThe acceleration due to gravity on the surface of the moon is `1.7ms^(-2)`. What is the time perioid of a simple pendulum on the surface of the moon, if its time period on the surface of earth is `3.5s ?` Take `g=9.8ms^(-2)` on the surface of the earth.
View SolutionConsider a pair of identical pendulums, which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of `2^(@)` to the right with the vertical , the other pendulum makes an angle of `1^(@)` to the left of the vertical. What is the phase difference between the pendulums?
View SolutionTwo pendulums differ in lengths by `22cm`. They oscillate at the same place so that one of them makes 30 oscillations and the other makes 36 oscillations during the same time. The length `(` in `cm)` of the pendulum are `:`
View SolutionThe time period of a simple pendulum on the surface of the earth is 4s. Its time period on the surface of the moon is
View SolutionA disc of radius R=10 cm oscillates as a physical pendulum about an axis perpendicular to the plane of the disc at a distance r from its centre. If `r=(R)/(4)`, the approximate period of oscillation is (Take `g=10ms^(-2)`)
View SolutionA simple pendulum is oscillating in a stationery lift. When the lift falls freely, the frequency of oscillations of the pendulum is
View SolutionA simple pendulum of length l and having a bob of mass M is suspended ina car. The car is moving on a circular track of radius R with a uniform speed v. If the pendulum makes small oscillations in a radial direction about its equilibrium, what will be its time period ?
View SolutionA simple pendulum executing SHM with a period of 6 s between two extreme positions B and C about a point O. if the length of the arc BC is 10 cm, how long will the pendulum take the move from position C to a position D towards O exactly midway between C and O?
View SolutionThe length of a second's pendulum on the surface of Earth in 1m. What will be the length of a second's pendulum on the moon?
View SolutionWhat is the length of a simple pendulum which ticks second?
View SolutionA rectangular block of mass m and area of cross-section A floats in a liquid of density `rho`. If it is given a small vertical displacement from equilibrium, it undergoes oscillation with a time period T. Then
View SolutionA particle oscillating under a force `vecF=-kvecx-bvecv` is a (k and b are constants)
View SolutionWhich of the following displacement-time graphs represent damped harmonic oscillation?
View SolutionWhich of the following energy-time graphs represents dajmped harmonic oscillator?
View SolutionA block of mass 200 g executing SHM under the influence of a spring of spring constant `k=90Nm^(-1)` and a damping constant `b=40gs^(-1)`. The time elapsed for its amplitude to drop to half of its initial value is (Given, ln `(1//2)=-0.693`)
View SolutionIn the question number 93, the time elapsed for its mechanical energy to drop half of its initial value is
View SolutionIn case of force oscillations of a body
View SolutionResonance is an example of
View SolutionIn case of a forced vibration, the resonance wave becomes very sharp when the
View SolutionAt resonance, the amplitude of forced oscillations is
View SolutionWhich of the following statements is correct?
View SolutionA particle of mass (m) is attached to a spring (of spring constant k) and has a natural angular frequency `omega_(0)`. An external force `R(t)` proportional to `cos omegat(omega!=omega_0)` is applied to the oscillator. The time displacement of the oscillator will be proportional to.
View Solution
MCQs questions and complete solutions for chapter OSCILLATIONS of MTG PHYSICS (ENGLISH) of Class 11
All Exercises from NCERT FINGERTIPS Class 11 PHYSICS OSCILLATIONS
- Assertion & Reason
- Assertion And Reason
- Damped Simple Harmonic Motion
- Energy In Simple Harmonic Motion
- Exemplar Problems
- Force Law For Simple Harmonic Motion
- Forced Oscillation And Resonance
- Higher Order Thinking Skills
- MCQs
- NCERT Exemplar
- Periodic And Oscillatory Motions
- Simple Harmonic Motion
- Simple Harmonic Motion And Uniform Circular Motion
- Some Systems Executing Simple Harmonic Motion
- Velocity And Acceleration In Simple Harmonic Motion