A spring balance has a scale that reads from 0 to 50 kg. the length of the scale is 20 cm. a block of mass m is suspended from this balance, when displaced and released, it oscillates with a period 0.5 s. the value of m is (Take g=10ms−2)
8 kg
12 kg
16 kg
20 kg
The correct Answer is:C
To solve the problem step by step, we will follow these instructions:
Step 1: Calculate the maximum force exerted by the spring balance
The maximum mass that the spring balance can read is 50 kg. To find the maximum force (F_max) exerted by this mass, we use the formula:
Fmax=m⋅g
Where:
- m=50kg
- g=10m/s2
Calculating:
Fmax=50kg×10m/s2=500N
Step 2: Calculate the spring constant (k)
The spring constant (k) can be calculated using the formula:
k=FmaxL
Where:
- Fmax=500N
- L=20cm=0.2m
Calculating:
k=500N0.2m=2500N/m
Step 3: Use the formula for the period of oscillation
The period (T) of oscillation for a mass-spring system is given by:
T=2π√mk
Step 4: Rearranging the formula to find mass (m)
Squaring both sides gives:
T2=4π2mk
Rearranging for mass (m):
m=T2⋅k4π2
Step 5: Substitute the known values
Given that T=0.5s and k=2500N/m:
m=(0.5)2⋅25004π2
Calculating:
m=0.25⋅25004π2
m=6254π2
Step 6: Calculate the numerical value of m
Using π≈3.14:
m=6254⋅(3.14)2
m=6254⋅9.8596
m=62539.4384≈15.8kg
Conclusion
The value of m is approximately 16 kg.
The maximum mass that the spring balance can read is 50 kg. To find the maximum force (F_max) exerted by this mass, we use the formula:
Fmax=m⋅g
Where:
- m=50kg
- g=10m/s2
Fmax=50kg×10m/s2=500N
The spring constant (k) can be calculated using the formula:
k=FmaxL
Where:
- Fmax=500N
- L=20cm=0.2m
k=500N0.2m=2500N/m
The period (T) of oscillation for a mass-spring system is given by:
T=2π√mk
Squaring both sides gives:
T2=4π2mk
Rearranging for mass (m):
m=T2⋅k4π2
Given that T=0.5s and k=2500N/m:
m=(0.5)2⋅25004π2
m=0.25⋅25004π2
m=6254π2
Using π≈3.14:
m=6254⋅(3.14)2
m=6254⋅9.8596
m=62539.4384≈15.8kg
The value of m is approximately 16 kg.
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills
8 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A spring balance has a scale that reads from 0 to 50kg. The length of the scale is 20cm. A body suspended from this spring, when displaced and released, oscillates with period of 0.60s. What is the weight of the body?
View SolutionA spring balance has a scale that reads from 0 to 50 kg. The length of the scale is 20 cm. A body suspended from this spring, when displaced and released, oscillates with a period of 0.6s. What is the weight of the body? When 50 kg is put, the extension of spring is 20 cm.
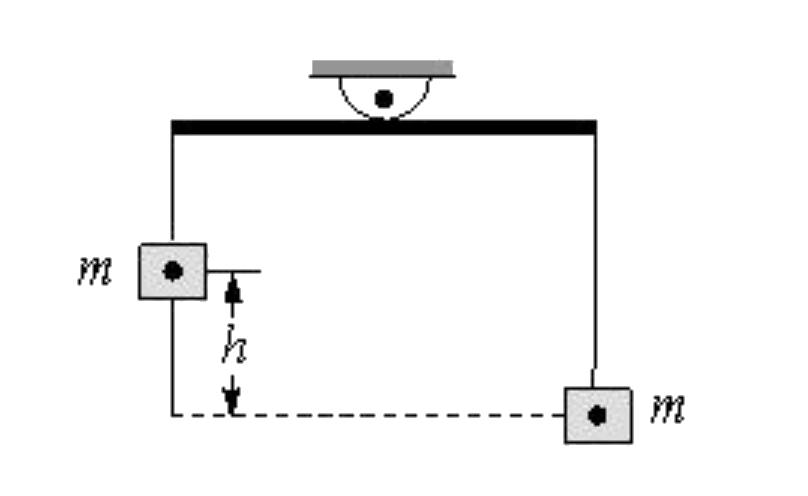
View SolutionTwo identical blocks of mass m are suspended from a beam balance whose scale pans differ in vertical height by h(h<<R), if R and ρ are the radius and density of the earth, then the error in weighing is
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
View SolutionA light spring balance hangs from the hook of the other light spring balance and a block of mass M kg hangs from the former one. Then the true statement about the scale reading is
View SolutionA light spring balance hangs from the hook of the other light spring balance and a block of mass M kg hangs from the former one. Then the true statement about the scale reading is
View Solution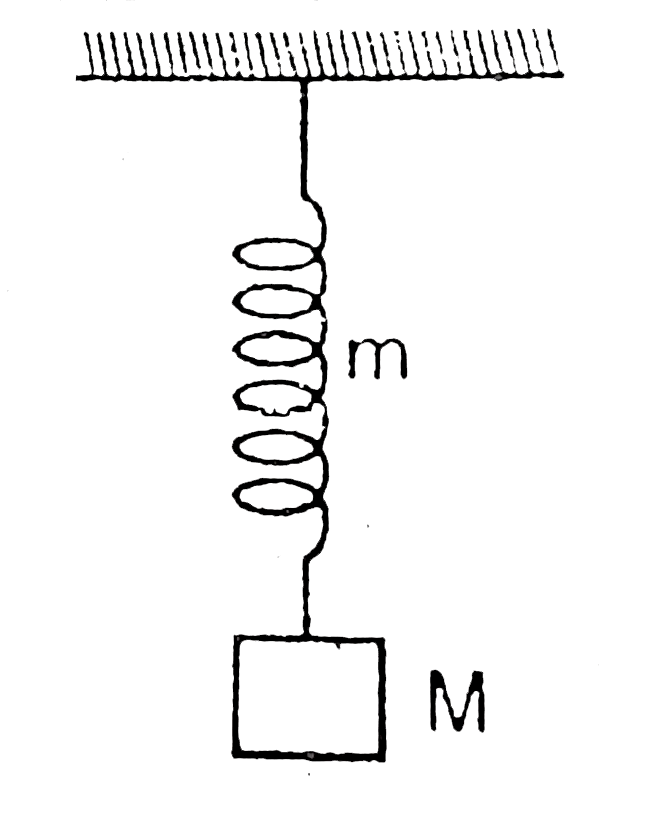
A block of M is suspended from a vertical spring of mass m as shown in the figure. When block is pulled down and released the mass oscillates with maximum velocity v.
View SolutionA beaker containing water is kept on a spring scale. The mass of water and beaker is 5 kg . A block of mass 2 kg and specific gravity 10 is suspended by means of thread from a spring balance as shown. The readings of scales S1 and S2 are respectively Take, g=10ms−2

View SolutionA spring balance reads forces in Newton. The scale is 20 cm long and read from 0 to 60 N. Find potential energy of spring when the scale reads 20 N.
View Solution
