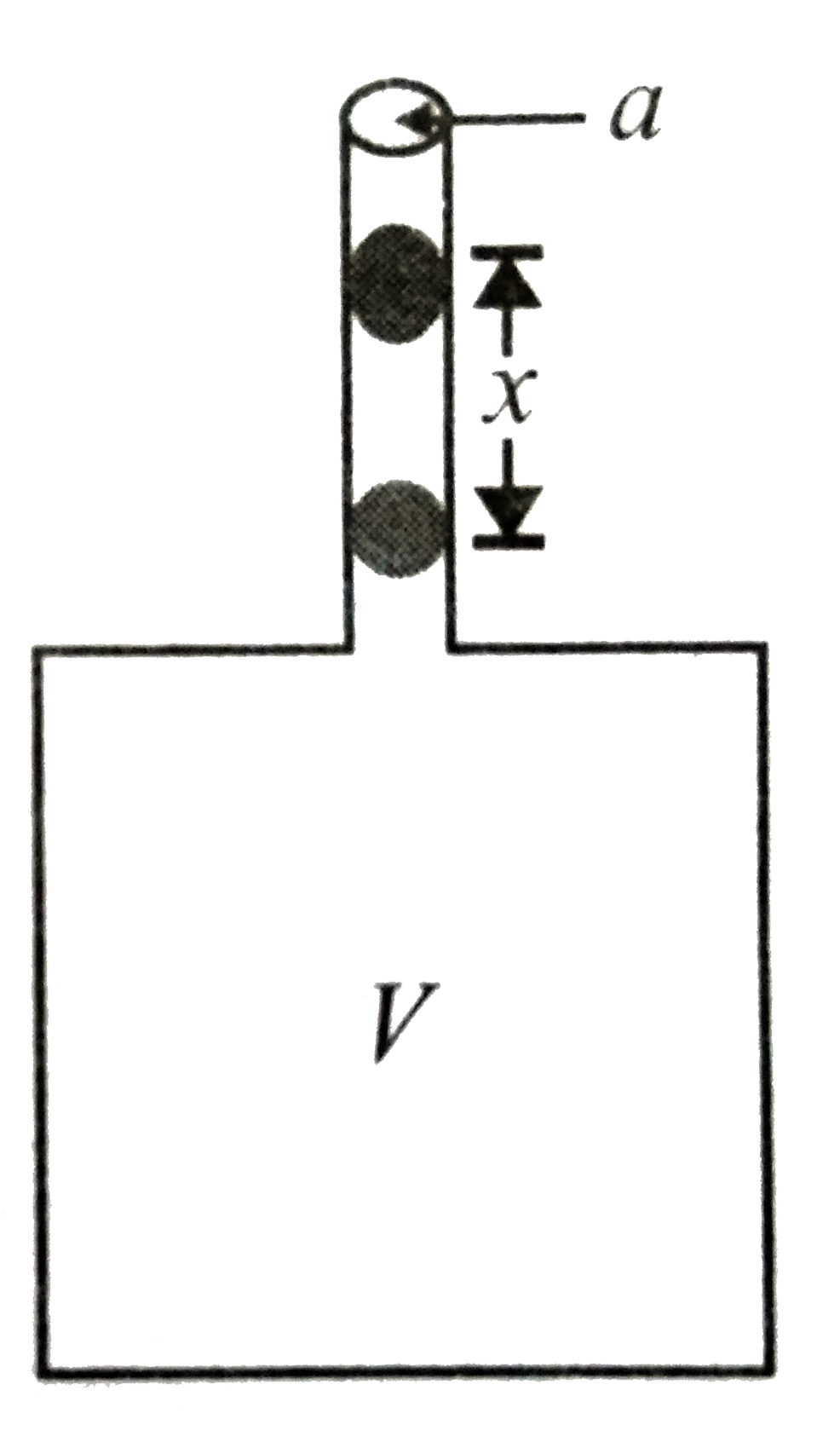
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure volume variations of air to be isothermal.
T=2π√Ba2mV
T=2π√BVma2
T=2π√mBVa2
T=2π√mVBa2
The correct Answer is:D

The situation is as shown in the figure. Let P be pressure of air in the chamber. When the ball is pressed down a distance x, the volume of air decreases from V to say V−ΔV. Hence the pressure increases from P to P+ΔP. the change in volume is ΔV=ax
The excess pressure ΔP is related to the bulk modulus B as
ΔP=−BΔVV
Restoring force on ball=excess pressure×cross-sectional
or F=−BaVΔV or F=−Ba2Vx (∵ΔV=ax)
or F=−kx, where k=Ba2V i.e., F∝−x
Hence, the motion of the ball is simple harmonic. if m is the ball, the time period of the SHM is
T=2π√mk or T=2π√mVBa2
Topper's Solved these Questions
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills
8 Videos
- OSCILLATIONS BOOK - NCERT FINGERTPS ENGLISHCHAPTER - OSCILLATIONS EXERCISE - Exemplar Problems
9 Videos
- MOTION IN A STRAIGHT LINEBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NCERT Exemplar
6 Videos
- PHYSICAL WORLDBOOK - NCERT FINGERTPS ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason
10 Videos
Similar Questions
A cylindrical log of wood of height h and area of cross-section A floats in water. It is pressed and then released. Show that lon would execute SHM with a time period. T=2π√mApg where, m is mass of the body and p is density of the liquid.
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
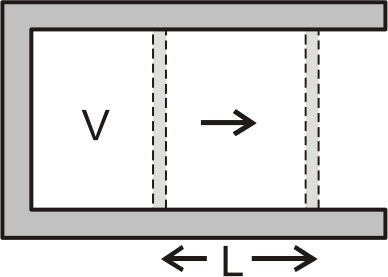
After the piston has moved by distance S. Its velocity is:
View SolutionFigure shows initial state of an ideal gas trapped in a container with conducting walls and a piston (mass m) which can move without any friction. The container is placed on point supports and its wall are conducting. Assuming that atmospheric pressure is P0 and the mass of the ideal gas is negligible as compared to the mass of the piston and the mass of container. Take the cross section area of piston to be A. The piston is slowly lifted by an external agent and held in its position. Let M be the maximum mass of container so that it may "lift off" while pulling the piston upwards and Pi be the pressure of ideal gas in initial state. Pick the correct choice:

View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).
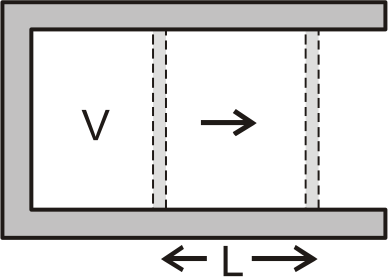
For the temperature of the gas to drop to one half of its original value. the piston will have to move by a distance:
View SolutionThe fixed non-conducting cylinder shown in figure has a noconducting heavy piston of mass M that can slide without friction. The area of piston is S and the cylinder is filled with an ideal gas (λ=1.5) with an initial volume V and an initial pressure P. Assume that the outside pressure on the piston is zero (vaccum). (Neglect acceleration due to gravity).

The initial acceleration of piston is:
View Solution
When a sound wave enters the ear, it sets the eardrum into oscillation, which in turn causes oscillation of 3 tiny bones in the middle ear called ossicles. This oscillation is finally transmitted to the fluid filled in inner portion of the ear termed as inner ear, the motion of the fluid disturbs hair cells within the inner ear which transmit nerve impulses to the brain with the information that a sound is present. The theree bones present in the middle ear are named as hammer, anvil and stirrup. Out of these the stirrup is the smallest one and this only connects the middle ear to inner ear as shown in the figure below. The area of stirrup and its extent of connection with the inner ear limits the sensitivity of the human ear consider a person's ear whose moving part of the eardrum has an area of about 50mm2 and the area of stirrup is about 5mm2. The mass of ossicles is negligible. As a result, force exerted by sound wave in air on eardum and ossicles is same as the force exerted by ossicles on the inner ear. Consider a sound wave having maximum pressure fluctuation of 4×10−2Pa from its normal equilibrium pressure value which is equal to 105Pa. Frequency of sound wave in air is 332ms. Velocity of sound wave in fluid (present in inner ear) is 1500ms. Bulk modulus of air is 1.42×105Pa. Bulk modulus of fluid is 2.18×109Pa.
Q. Find the pressure amplitude of given sound wave in the fluid of inner ear.
View SolutionAn ideal monoatomic gas is enclosed in a fixed horizontal adiabatic cylinder of cross sectional area A. The cylinder is fitted with an adiabatic piston of mass m (attached to one end of a spring as shown) which can move horizontally without friction inside the cylinder. In equilibrium, the spring is in natural length and pressure and volume are P0 and V0 respectively. The piston is slightly displaced from equilibrium and released. Then, frequency of small oscillation is

View SolutionIf a body moves through a liquid or a gas then the fluid applies a force on the body which is called drag force. Direction of the drag force is always opposite to the motion of the body relative to the fluid. At low speeds of the body, drag frog (FP) is directly proportional to the speed.
FD=kv
What K is a proportionally constant and it depends upon the dimension of the body moving in air at relatively high speeds, the drag force applied by air an the body is proportional to v2
Where this proportionally constant K can be given by
K2ρCA
Where ρ is the density of air
C is another constant givig the drag property of air
A is area of cross-section of the body
Consider a case an object of mass m is released from a height h and it falls under gravity. As it's speed increases the drag force starts increasing on the object. Due to this at some instant, the object attains equilibrium. The speed attained by the body at this instant is called "terminal speed" of the body.
Assume that the drag force applied by air on the body follows the relation FD=kv,neglect the force by buoyancy applied by air on the body then answer the following questions.
What is the pattern of acceleration change of the body ?
View SolutionIf a body moves through a liquid or a gas then the fluid applies a force on the body which is called drag force. Direction of the drag force is always opposite to the motion of the body relative to the fluid. At low speeds of the body, drag frog (FP) is directly proportional to the speed.
FD=kv
What K is a proportionally constant and it depends upon the dimension of the body moving in air at relatively high speeds, the drag force applied by air an the body is proportional to v2
Where this proportionally constant K can be given by
K2ρCA
Where ρ is the density of air
C is another constant givig the drag property of air
A is area of cross-section of the body
Consider a case an object of mass m is released from a height h and it falls under gravity. As it's speed increases the drag force starts increasing on the object. Due to this at some instant, the object attains equilibrium. The speed attained by the body at this instant is called "terminal speed" of the body.
Assume that the drag force applied by air on the body follows the relation FD=kv,neglect the force by buoyancy applied by air on the body then answer the following questions.
What is the terminal speed of the object ?
View Solution
When a sound wave enters the ear, it sets the eardrum into oscillation, which in turn causes oscillation of 3 tiny bones in the middle ear called ossicles. This oscillation is finally transmitted to the fluid filled in inner portion of the ear termed as inner ear, the motion of the fluid disturbs hair cells within the inner ear which transmit nerve impulses to the brain with the information that a sound is present. The theree bones present in the middle ear are named as hammer, anvil and stirrup. Out of these the stirrup is the smallest one and this only connects the middle ear to inner ear as shown in the figure below. The area of stirrup and its extent of connection with the inner ear limits the sensitivity of the human ear consider a person's ear whose moving part of the eardrum has an area of about 50mm2 and the area of stirrup is about 5mm2. The mass of ossicles is negligible. As a result, force exerted by sound wave in air on eardum and ossicles is same as the force exerted by ossicles on the inner ear. Consider a sound wave having maximum pressure fluctuation of 4×10−2Pa from its normal equilibrium pressure value which is equal to 105Pa. Frequency of sound wave in air is 332ms. Velocity of sound wave in fluid (present in inner ear) is 1500ms. Bulk modulus of air is 1.42×105Pa. Bulk modulus of fluid is 2.18×109Pa.
Q. This person (without hearing aid machine) is sitting inside a busy restaurant where average sound intensity is 3.2×10−5Wm2. How much energy in the form of sound is taken up by the person in his meal time of 1 h?
View Solution
