For the circle x2+y2=r2, find the value of r for which the area enclosed by the tangents drawn from the point P(6,8) to the circle and the chord of contact and the chord of contact is maximum.
The given circle is x2+y2=r2. From point (6,8), tangents are drawn to this circle.
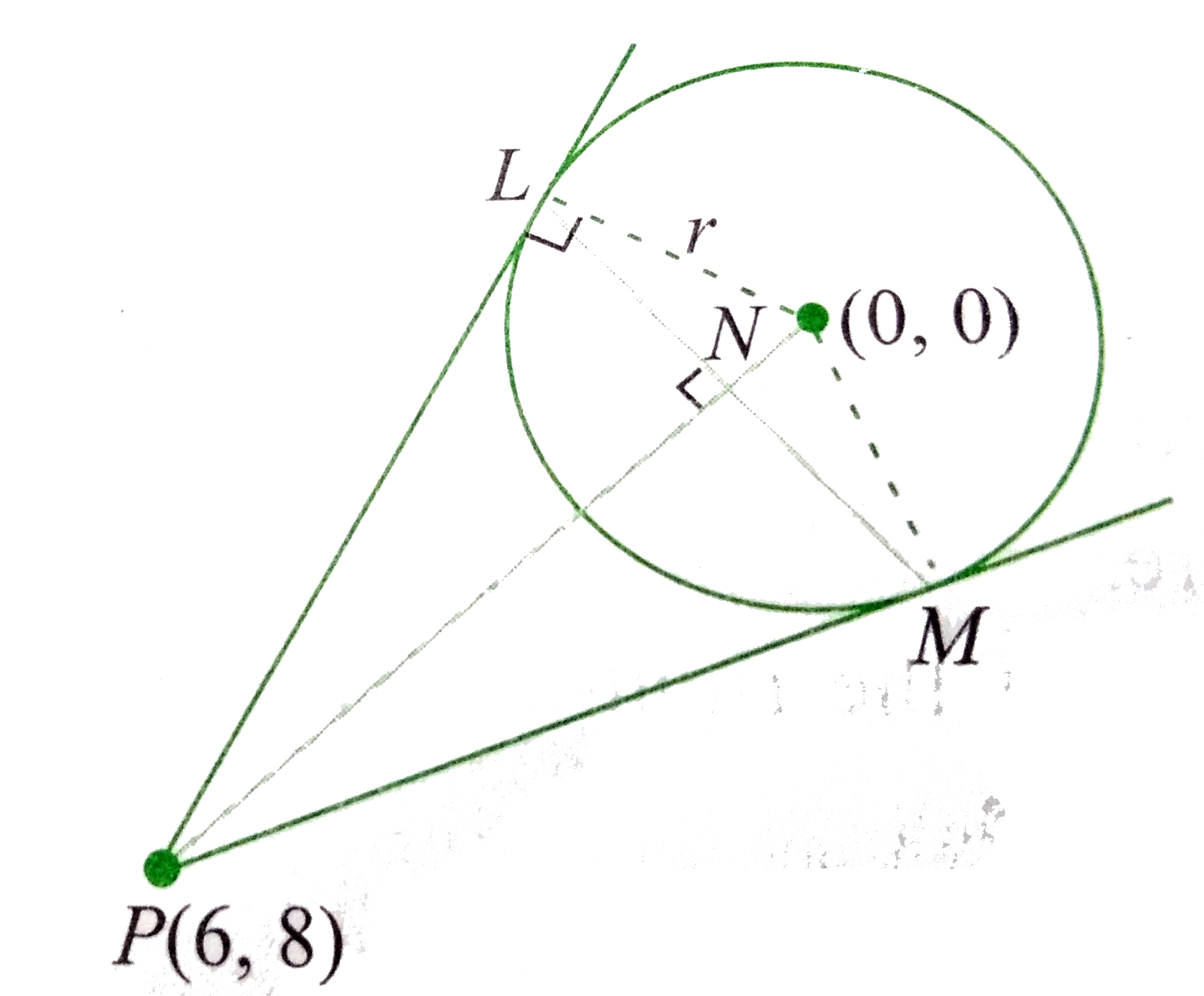
Then, the length of tangent is
PL=√62+82−r2=√100−r2
Also, the equation of chord of contact LM is 6x+8y−r2=0.
PN= Length of ⊥ from P to LM
=36+64−r2√36+64=100−r210
Now, in right - angles ΔPLN
LN2=PL2−PN2
=(100−r2)−(100−r2)2100=(100−r2)r2100
or LN=r√100−r210
∴LM=r√100−r25 (∵LM=2LN)
∴ Area of ΔPLM=Δ=12×LM×PN
=12×r√100−r25×100−r210
=1100[r(100−r2)3/2]
For the maximum value of Δ, we should have
dΔdr=0
or 1100[(100−r2)3/2+r32(100−r2)1/2(−2r)]=0
or (100−r2)1/2[100−r2−3r2]=0
i.e., r=10 or r=5
But r=10 gives the length of tangent PL. Therefore, r cancel (=)10.
Hence, r=5.
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.1
Explore 1 Video
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.2
Explore 2 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:MATRIX MATCH TYPE
Explore 7 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
Find the area of the triangle formed by two tangents drawn from (3,5) to the circle x2+y2=16 and the chord of contact of (3,5)
View SolutionFind the area of the triangle formed by the tangents drawn from the point (4,6) to the circle x2+y2=25 and their chord of contact.
Answer: 405√352 sq. units
View SolutionFind the area of the triangle formed by the tangents from the point (4, 3) to the circle x2+y2=9 and the line joining their points of contact.
View SolutionFind the area of the triangle formed by the tangents from the point (4, 3) to the circle x2+y2=9 and the line joining their points of contact.
View SolutionThe area of the triangle formed by the tangents from (1,3) to the circle x2+y2−4x+6y+1=0 and its chord of contact is
View SolutionTangents are drawn from the point (-1, 2) to the parabola y2=4x The area of the triangle for tangents and their chord of contact is
View SolutionTangents are drawn from the point (-1, 2) to the parabola y2=4x The area of the triangle for tangents and their chord of contact is
View SolutionThe area of triangle formed by the tangents from the point (3, 2) to the hyperbola x2−9y2=9 and the chord of contact w.r.t. the point (3, 2) is_____________
View SolutionThe points of contact of the tangents drawn from the point (4, 6) to the parabola y2=8x
View SolutionThe length of the chord of contact of the tangents drawn from the point (−2,3) to the circle x2+y2−4x−6y+12=0 is:
View Solution

