Question

Tangents are drawn to the circle $x^2+y^2=a^2$
from two points on the axis of $x,$
equidistant from the point $(k,0)\stackrel{.}{}$
Show that the locus of their intersection is $k{y}^2=a^2(k-x)\stackrel{.}{}$

Explanation

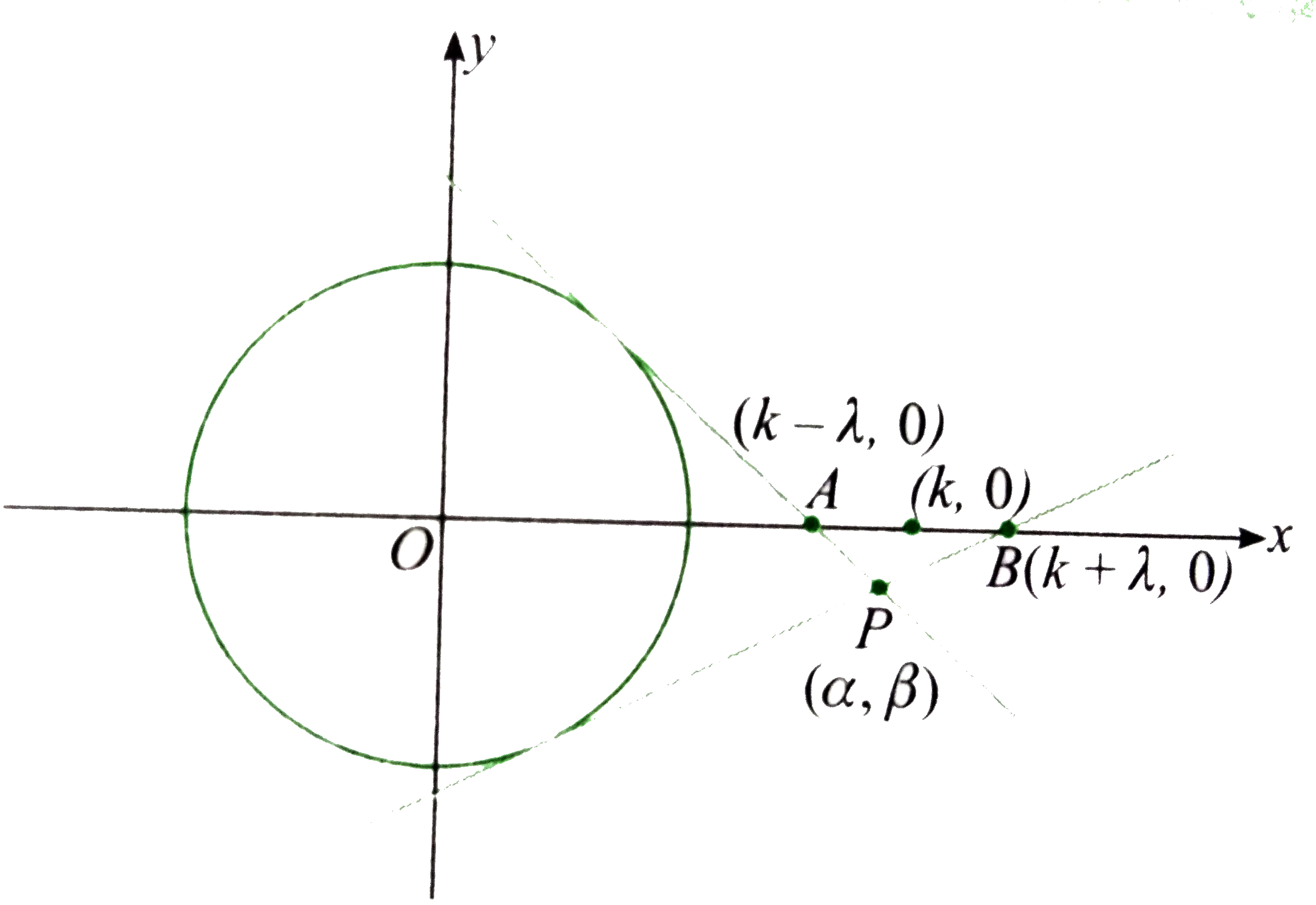
As shown in figure , point A and B are equidistant from point (k,0).
Tangents drawn from point A and B intersect at point `P(alpha,beta)`.
Equation of pair of tangents from point P is
`(x^(2)+y^(2)-a^(2))(alpha^(2)+beta^(2)-a^(2))=(alpha x +betay-a^(2))^(2)` (Using `T^(2)=S S_(1))`
This equation is satisfied by points A and B .
`:. ((k-lambda)^(2)-a^(2))(alpha^(2)+beta^(2)-a^(2))=(alpha(k-lambda)-a^(2))^(2)` (1)
and `((k+lambda)^(2)-a^(2))(alpha^(2)+beta^(2)-a^(2))=(alpha(k+lambda)-a^(2))^(2)` (2)
Subtracting (1) and (2) , we get
`(alpha^(2)+beta^(2)-a^(2))(4klambda)=[(k+lambda)alpha-a^(2)+(k-lambda)alpha-a^(2)][(k+lambda)alpha-(k-lambda)alpha]=[2(k alpha-a^(2))][2 lambda alpha]=4 lambda alpha[k alpha -a^(2)]`
`implies k( alpha^(2)+beta^(2)-a^(2))=k alpha^(2)-a^(2) alpha`
`implies k beta^(2)=a^(2)(k-alpha)`
Hence, the locu is `ky^(2)=a^(2)(k-x)`