A circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
The equation of the circle is
(x−1)2+(y−1)2=1
or x2+y2−2x−2y+1=0 (1)
Let the equation of the variable straight line through origin be
y=mx (2)
This line intersects the cricle at two points D and E.
Distance of line from point B(0,1) is
BM=|m(0)−1|√1+m2=1√1+m2
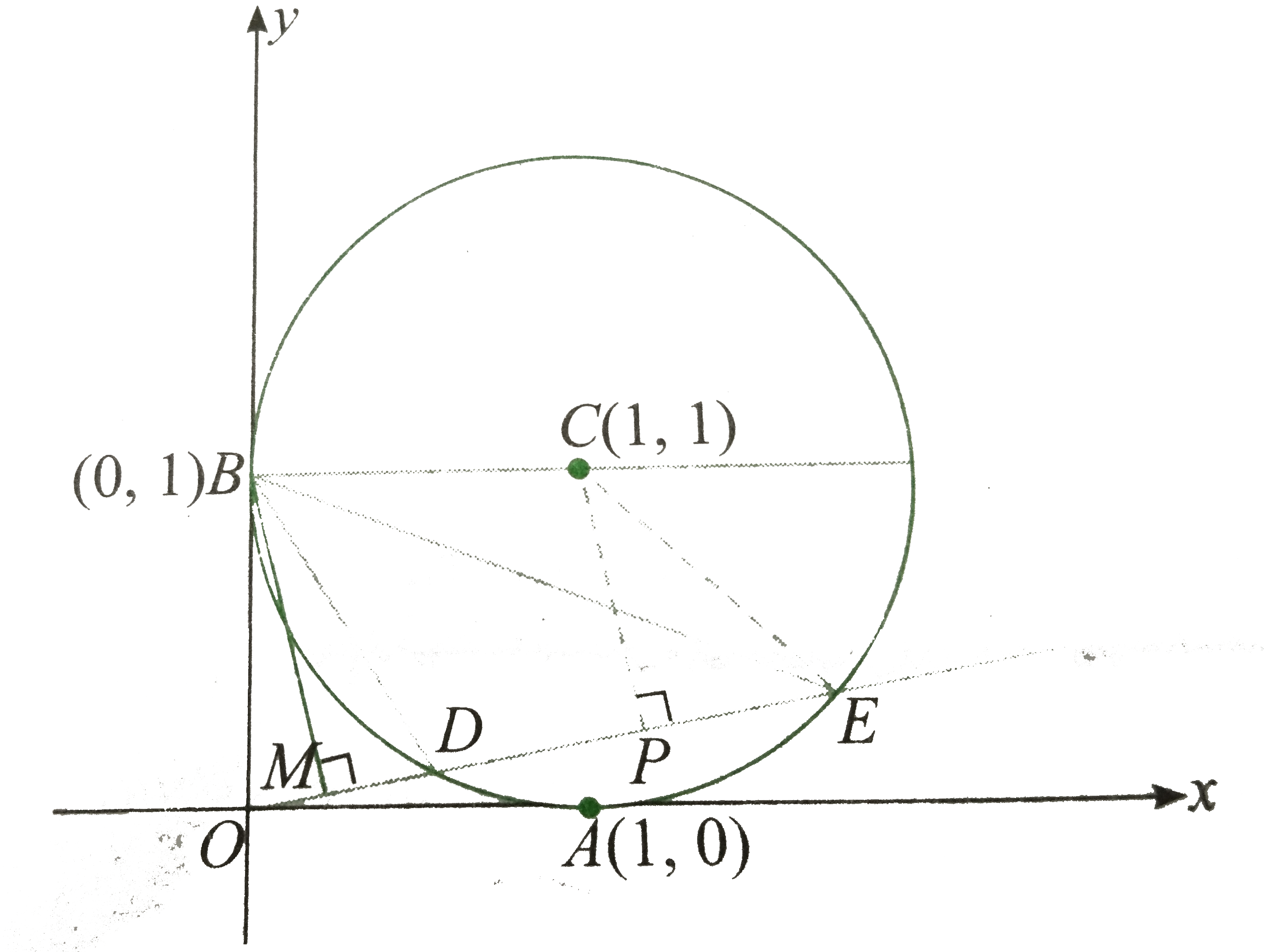
Also, CP=|m(1)−1|√1+m2=|m−1|√1+m2
∴DE=2PE=2√CE2−CP2=2√1−(m−1)21+m2=2√2m1+m2
∴Area of triangle DEB.
Δ=12BM×DE
=121√1+m2×2√2m1+m2=√2m1+m2
Differentiating Δ w.r.t. m, we get
dΔdm=√2⎡⎢⎣12√m(1+m2)−2m√m(1+m2)2⎤⎥⎦=1−3m2√2√m(1+m2)2
If dΔdm=0 , then m=1√m, whichi is point of maxima.
Therefore, area is maximum if m=1√3.
Topper's Solved these Questions
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.1
Explore 1 Video
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:CONCEPT APPLICATION EXERCISE 4.2
Explore 2 Videos
- CIRCLE Book:CENGAGE ENGLISHChapter:CIRCLE Exercise:MATRIX MATCH TYPE
Explore 7 Videos
- BINOMIAL THEOREMBook:CENGAGE ENGLISHChapter:BINOMIAL THEOREMExercise:Matrix
Explore 4 Videos
- CIRCLESBook:CENGAGE ENGLISHChapter:CIRCLESExercise:Comprehension Type
Explore 8 Videos
Similar Questions
If a line passing through the origin touches the circle (x−4)2+(y+5)2=25 , then find its slope.
View SolutionA line L passing through the focus of the parabola y2=4(x−1) intersects the parabola at two distinct points. If m is the slope of the line L, then −1<m<1 (b) m<−1 or m>1 m∈R (d) none of these
View SolutionA line L passing through the focus of the parabola y2=4(x−1) intersects the parabola at two distinct points. If m is the slope of the line L, then (a) −1<m<1 (b) m<−1 or m>1 (c) m∈R (d) none of these
View SolutionCircle with centre C (1, 1) passes through the origin and intersects the x-axis at A and y-axis at B. The area of the part of the circle that lies in the first quadrant is
View SolutionA variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionIf the radius of the circle passing through the origin and touching the line x+y=2 at (1,1) is r units, then the value of 3√2r is
View SolutionA variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is
View SolutionA variable circle passes through the fixed point (2, 0) and touches y-axis Then, the locus of its centre, is
View SolutionIf a circle passes through the point of intersection of the lines x+y+1=0 and x+λy−3=0 with the coordinate axis, then find the value of λ .
View SolutionA line L passing through the focus of the parabola (y−2)2=4(x+1) intersects the two distinct point. If m be the slope of the line I,, then
View Solution