Lines 5x+12y−10=0 and 5x−12y−40=0 touch a circle C1 of diameter 6. If the center of C1, lies in the first quadrant then the equation of the circle C2, which is concentric with C1, and cuts intercept of length 8 on these lines
According to the question, circles are drawn as shown in the figure.
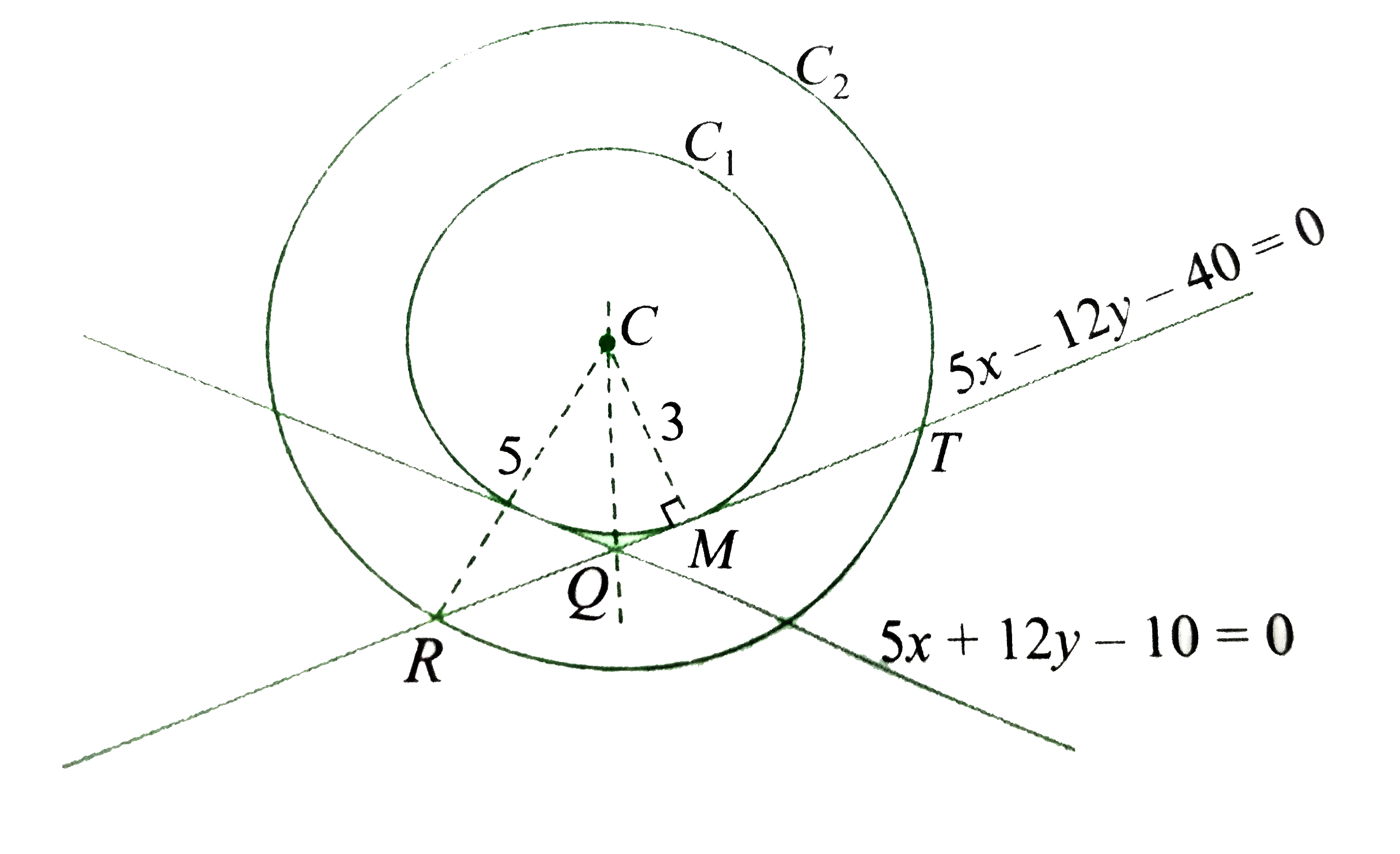
Centre of the circles lies on one of the angle bisectors of the given lines.
5x+12y−1013=±5x−12y−4013
or 24y=−30 and 10x=50
But centre lies in first quadrant.
So, for centre , x=5.
Distance of centre (C(5,y) from the line 5x+12y−10=0 is 3.
∴5(5)+12y−1013=±13
∴y=2 (As centre lies in first quadrant)
Sol, centre is (5,2).
Alsok, in right angles triangle CMR, CR=5( as RM=4).
Hence, equation of circle is (x−5)2−(y−2)2=52.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.2
2 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Find the equation of a circle whose centre is (3,-1) and which cuts off a chord 6 length 6 units on the line 2x-5y + 18 = 0.
View SolutionFind the equation of the circle which is concentric with x2+y2+8x+12y+15=0 and passing through (2,3).
View SolutionFind the equation of the circle which has centre C (3, 1) and which touches the line 5x-12y + 10 = 0.
View SolutionThe equation of the circle withcentre at (4,3) and touching the line 5x−12y−10=0 is
View SolutionFind the equation of the circle centre C(1,2) and tangent x+y-5 =0
View SolutionIf the line 2x−y+1=0 touches the circle at the point (2,5) and the centre of the circle lies in the line x+y−9=0. Find the equation of the circle.
View SolutionFind the equation of the circle which has its centre at the point (3,4) and touches the straight line 5x+12y−1=0.
View SolutionFind the equation of the circle having centre at (3,−4) and touching the line 5x+12y−12=0.
View SolutionFind the equation of the circle having centre at (3,−4) and touching the line 5x+12y−12=0.
View SolutionFind the equation of the circle which touches the lines x=0,y=0andx=4 and lies in the first quadrant.
View Solution
