Question

If eight distinct points can be found on the curve $\left|x\right|+\left|y\right|=1$
such that from eachpoint two mutually perpendicular tangents can be
drawn to the circle $x^2+y^2=a^2,$
then find the range of $a\stackrel{.}{}$

Explanation

`|x| +|y|=1` forms a square having vertices at A(1,0), B(0,1),C(-1,0) and D(0,-1).

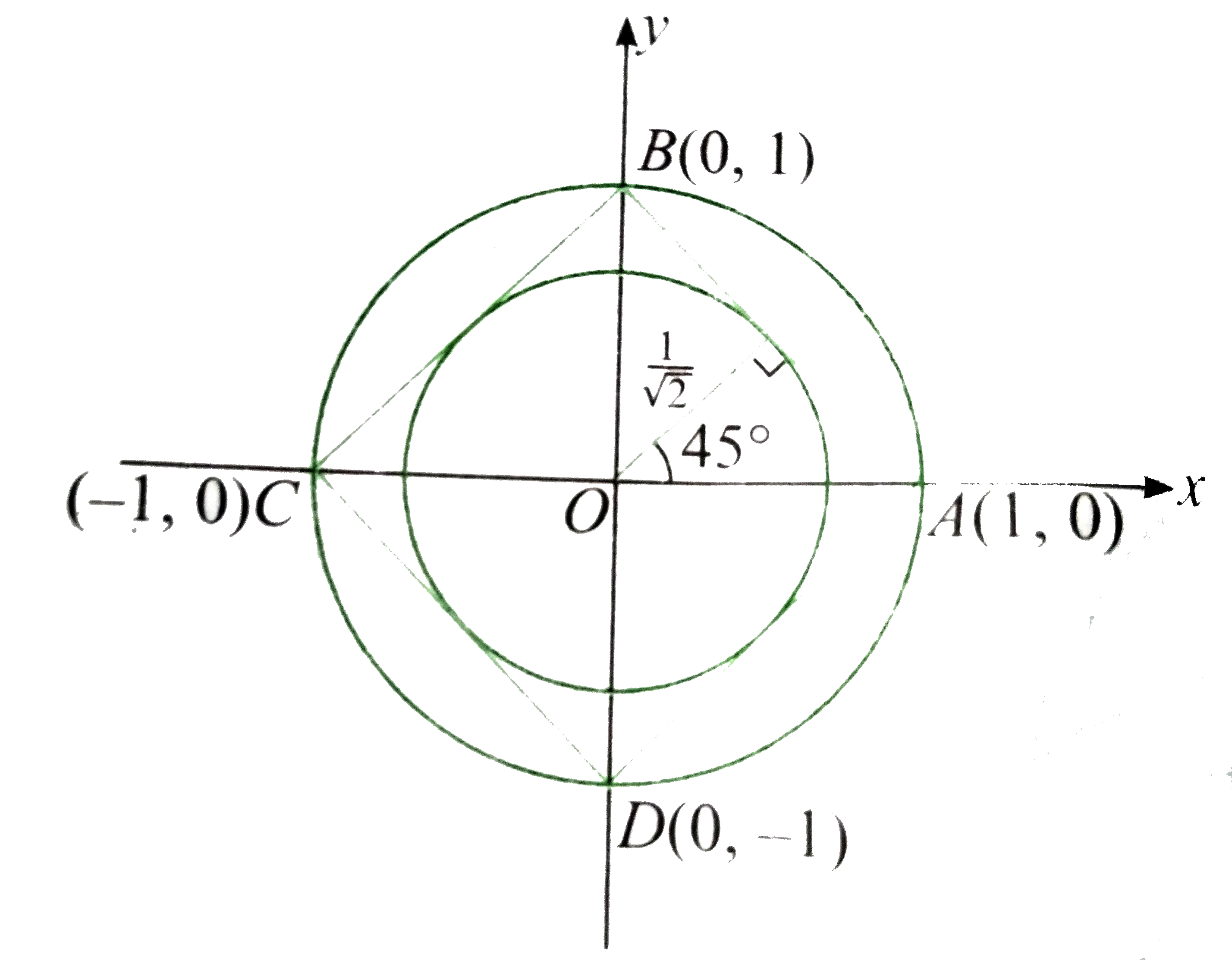
Mutually perpendicular tangents meet on the director circle whose equation is `x^(2)+y^(2)=2a^(2)`.
Equation of circle passing through vertices of square is `x^(2)+y^(2)=1` and its radius is 1.
Equation of circle inscribed in the circle is `x^(2)+y^(2)=(1)/(2)` and its radius is `(1)/(sqrt(2))`.
For eight points on the square, radius of the director circle must lie between `(1)/(sqrt(2))` and 1.
Thus, `(1)/(sqrt(2))lt sqrt(2)a lt1`.
Hence, `(1)/(sqrt(2))lt alt (1)/(sqrt(2))`