Let P be any moving point on the circle x2+y2−2x=1.AB be the chord of contact of this point w.r.t. the circle x2+y2−2x=0 . The locus of the circumcenter of triangle CAB(C being the center of the circle) is 2x2+2y2−4x+1=0 x2+y2−4x+2=0 x2+y2−4x+1=0 2x2+2y2−4x+3=0
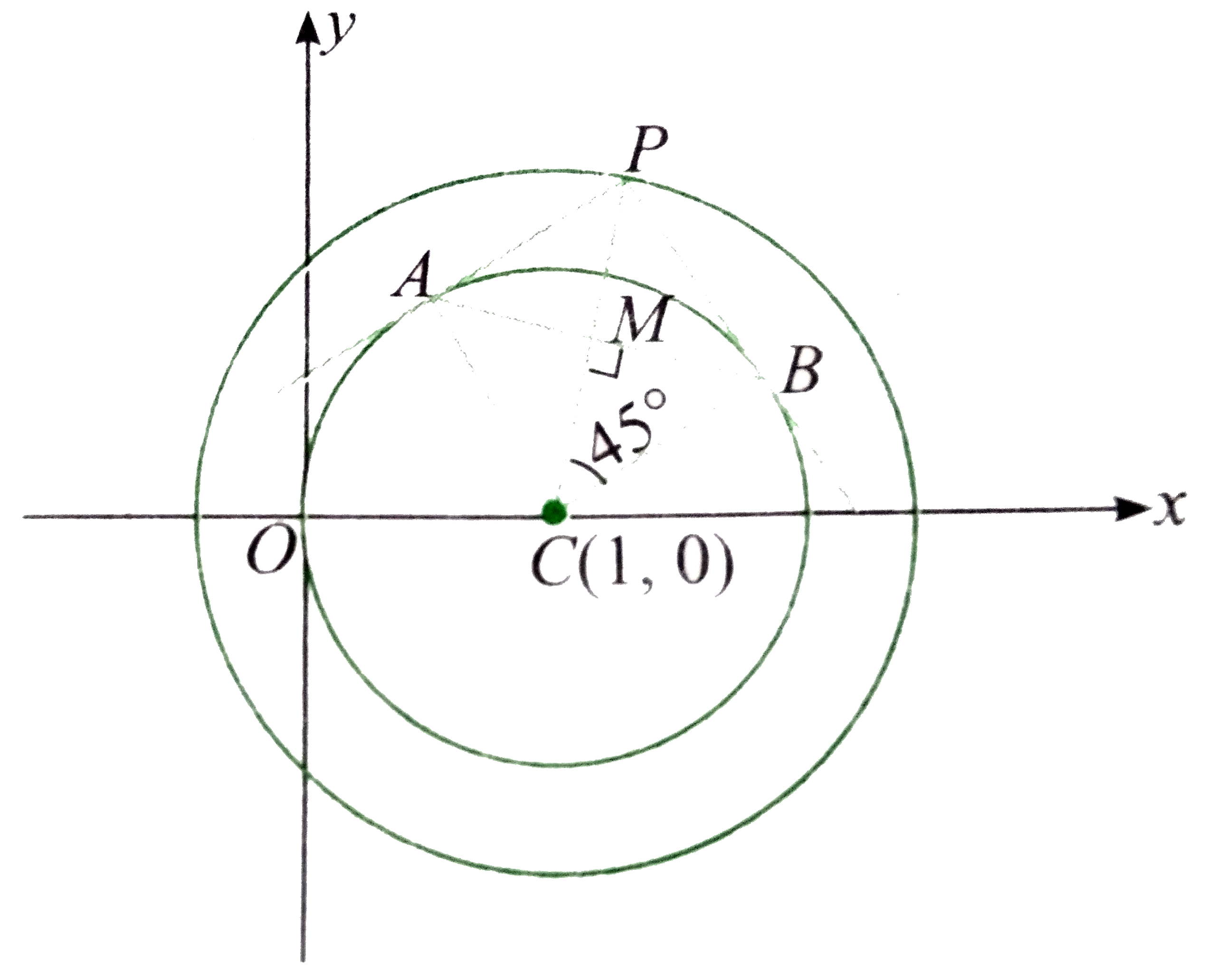
The two circles are
(x−1)2+y2=1 (1)
(x−1)2+y2=2 (2)
Clearly, the second circle is the director circle of the first circle.
∴∠AB=90∘
S, APBC is square.
Now, circumcentre of the right-angled triangle CAB will be midpoint of hypotenuse.
Let midpoint of AB be M(h,k).
Now, CM=CBsin45∘=1√2
So, (h−1)2+k2=12
Hence, locus of M is (x−1)2+y2=12
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.2
2 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
Let P be any moving point on the circle x2+y2−2x=1.AB be the chord of contact of this point w.r.t. the circle x2+y2−2x=0 . The locus of the circumcenter of triangle CAB(C being the center of the circle) is a.2x2+2y2−4x+1=0 b.x2+y2−4x+2=0 c.x2+y2−4x+1=0 d.2x2+2y2−4x+3=0
View SolutionThe chord of contact of (3,-1) w.r.t the circle x2+y2+2x−4y+1=0 is
View SolutionThe chord of contact of (2,1) w.r.t to the circle x2+y2+4x+4y+1=0 is
View SolutionThe chord of contact of (1,2) with respect to the circle x2+y2−4x−6y+2=0 is
View SolutionLength of chord of contact of point (4,4) with respect to the circle x2+y2−2x−2y−7=0 is
View SolutionThe radical centre of the circles x2+y2=9,x2+y2−2x−2y−5=0,x2+y2+4x+6y−19=0 is
View SolutionFind the radical centre of the following circles
x2+y2−4x−6y+5=0
x2+y2−2x−4y−1=0
x2+y2−6x−2y=0
View SolutionThe mid point of the chord x−2y+7=0 w.r.t the circle x2+y2−2x−10y+1=0 is
View SolutionFor the circle x2+y2−4x+2y+c=0 radius is 4 then c=
View SolutionFind the length of the common chord of the circles x2+y2+2x+6y=0 and x2+y2−4x−2y−6=0
View Solution
