A solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
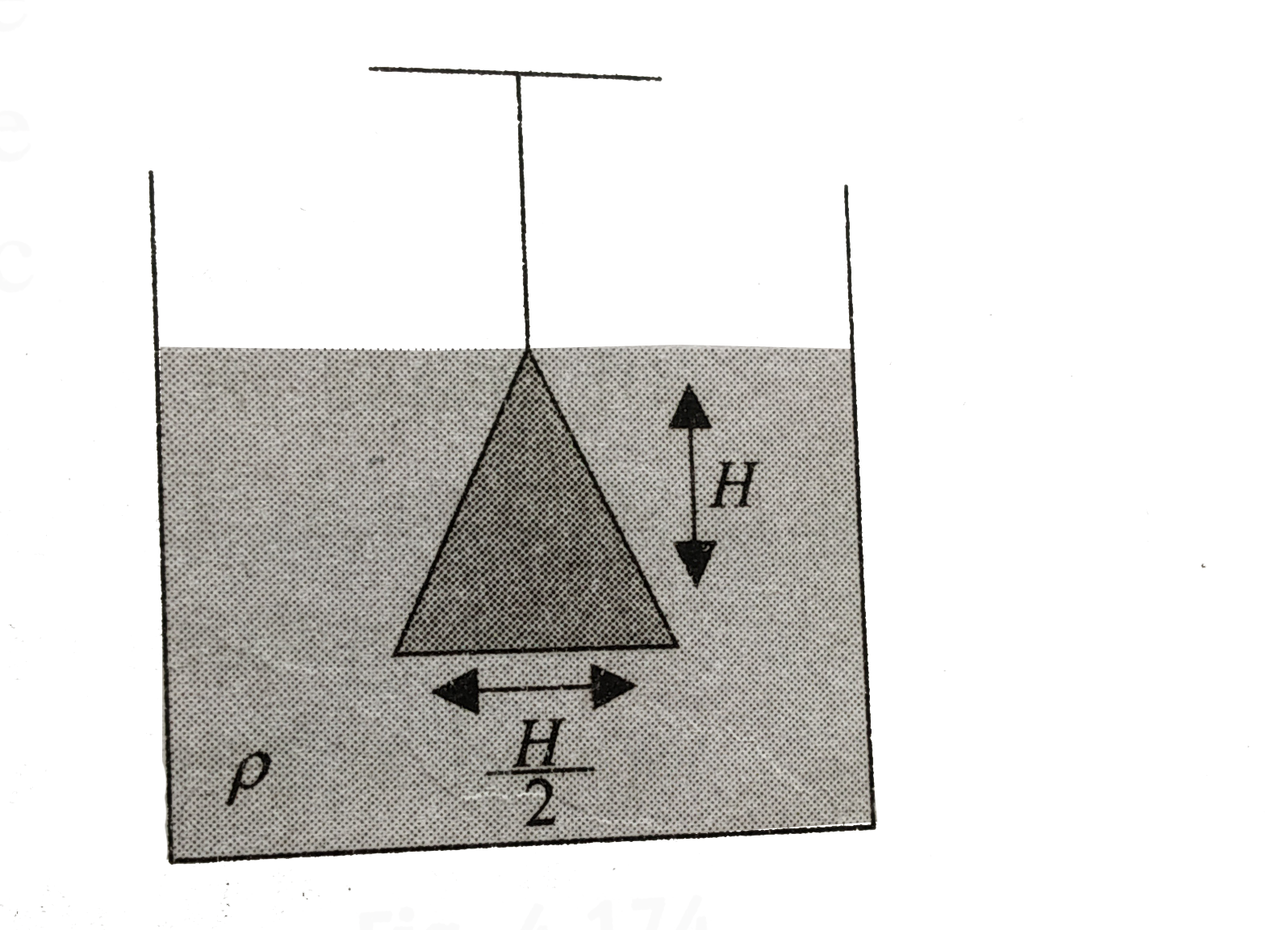
There will be only vertically downard force on the curved surface of the cone as the horizontal force will be cancelled. Let this force be F
Buoyoney force =(P0+SgH)πR2−F
1/3πR2HSg=(P0+SgH)πR2−F
F=πR23(3P0+2SgH)
Similar Questions
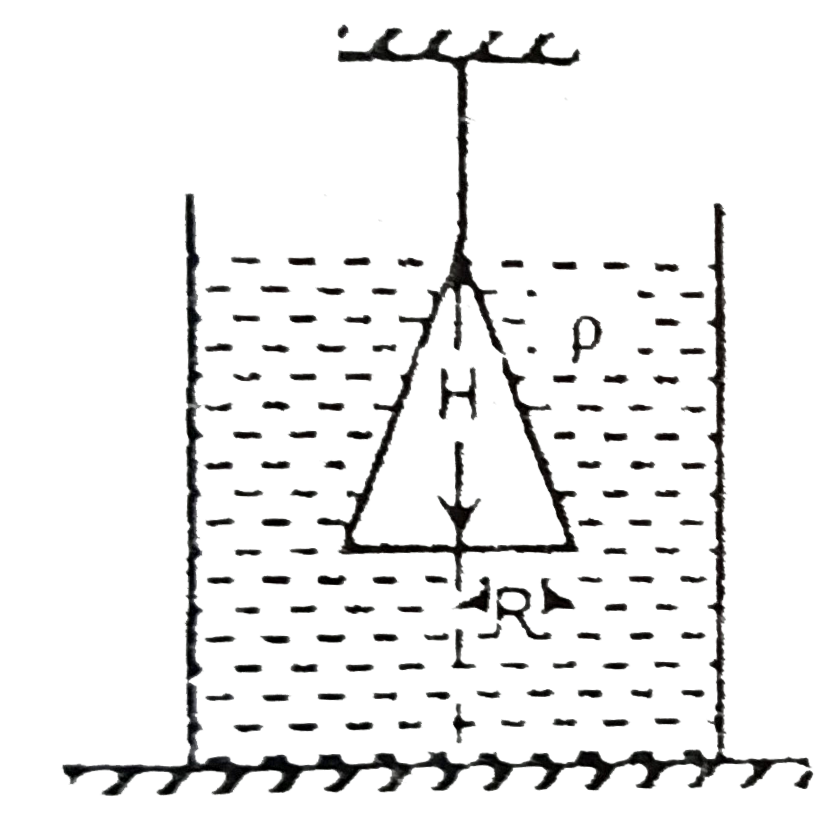
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
View SolutionA beaker is filled with a liquid of density ρ upto a height h If the beaker is at rest, the mean pressure at the walls is:
View SolutionA solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and diameter 1 cm. Find the number of cones formed.
View SolutionThe cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.

View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionConsider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

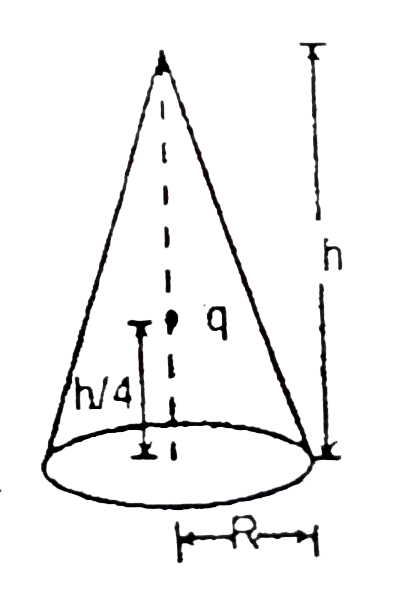
View SolutionA charge q is placed at a height h4 from the base of a cone of height h and radius R as shown in figure. Calculate the flux linked with the curved surface of the cone.
View SolutionA Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View SolutionA solid sphere of radius r is melted and cast into the shape of a solid cone of height r , the radius of the base of the cone is
View Solution
