
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)
πr2dg(H−r3)
2πr2dg(H−2r3)
πr2dg(2H−r3)
πr2dg(2H−2r3)
The correct Answer is:A
Force due to liquid on curved surface =F
F= weight of liquid above the cone
F=(πr2H−13πr3)dg=πr2dg[H−r3]
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:integer Type Questions
Explore 25 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Level 1 (H.W)
Explore 55 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Paragraph Type Questions
Explore 5 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
A triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
View SolutionA solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
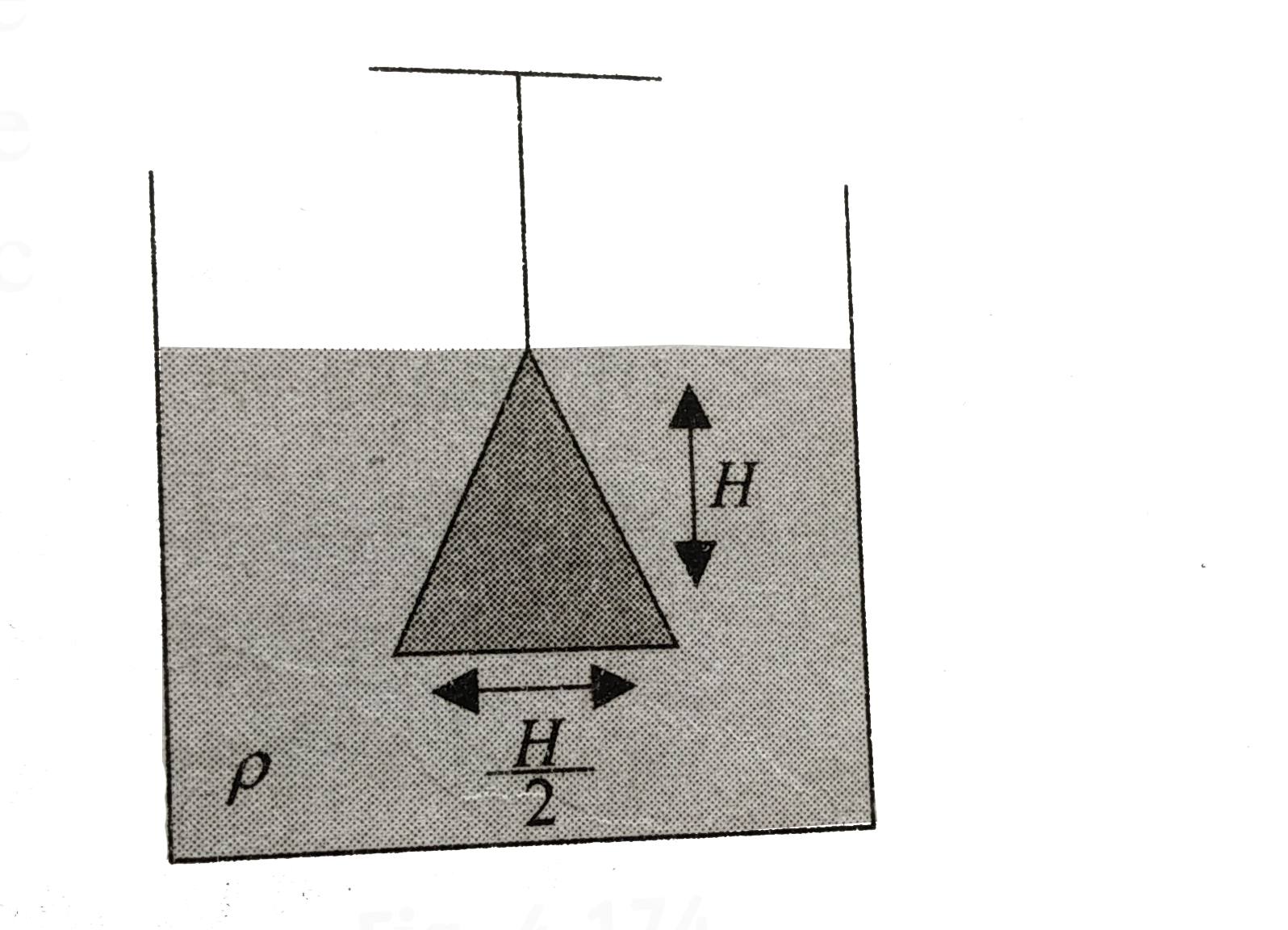
View Solution
Knowledge Check
The cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.
 ANet force on the cone by the liquid is equal to buoyancy force on the cone.BForce on the bottom surfae of the cone is more than buoyancy force on the cone.CNet force on the slant surface of the cone is more than buoyancy force on the cone.DNet force on the slant surface of the cone is less than buoyancy force on the cone.
ANet force on the cone by the liquid is equal to buoyancy force on the cone.BForce on the bottom surfae of the cone is more than buoyancy force on the cone.CNet force on the slant surface of the cone is more than buoyancy force on the cone.DNet force on the slant surface of the cone is less than buoyancy force on the cone.A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
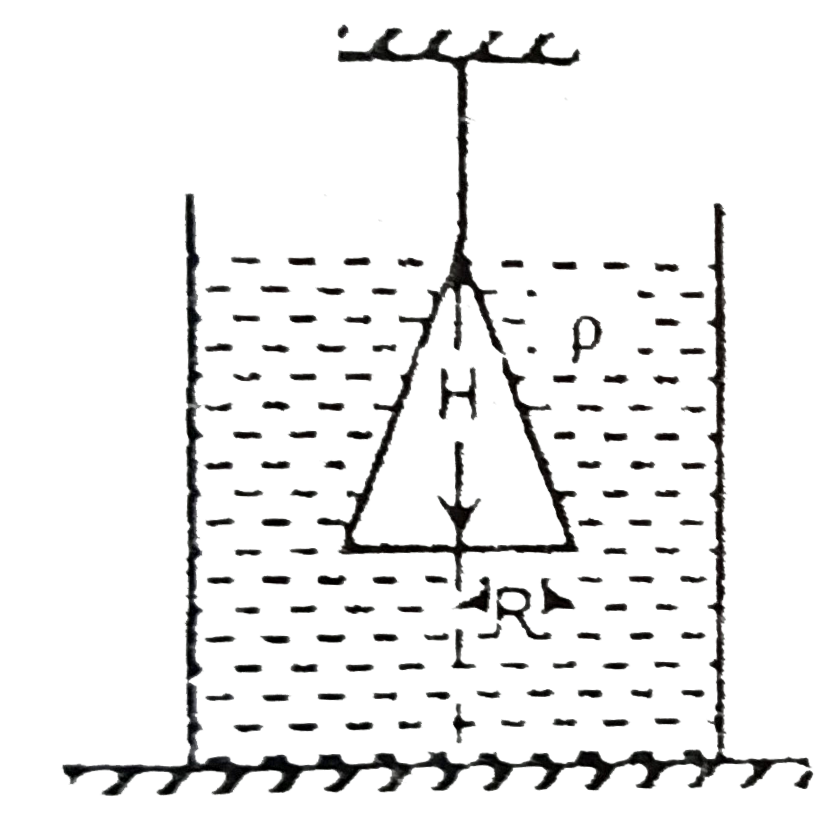 AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2A beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
AhρgBhρ(g+a)Chρ(g−a)D2hρg(g−ag+a)
A ring of radius r, and weight W is lying on a liquid surface . If the surface tension of the liquid is T , then the minimum force required to be applied in order to lift the ring up
View SolutionThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
View SolutionDensity of a liquid varies with depth as ρ=αh. A small ball of density ρ0 is released from the free surface of the liquid. Then
View SolutionA sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
View SolutionA hemispherical portion of radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass M. It is suspended by a string in a liquid of density ρ where it stays vertical. The upper surface of the cylinder is at a depth h below the liquid surface. The force on the bottom of the cylinder by the liquid is

View Solution

