A solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
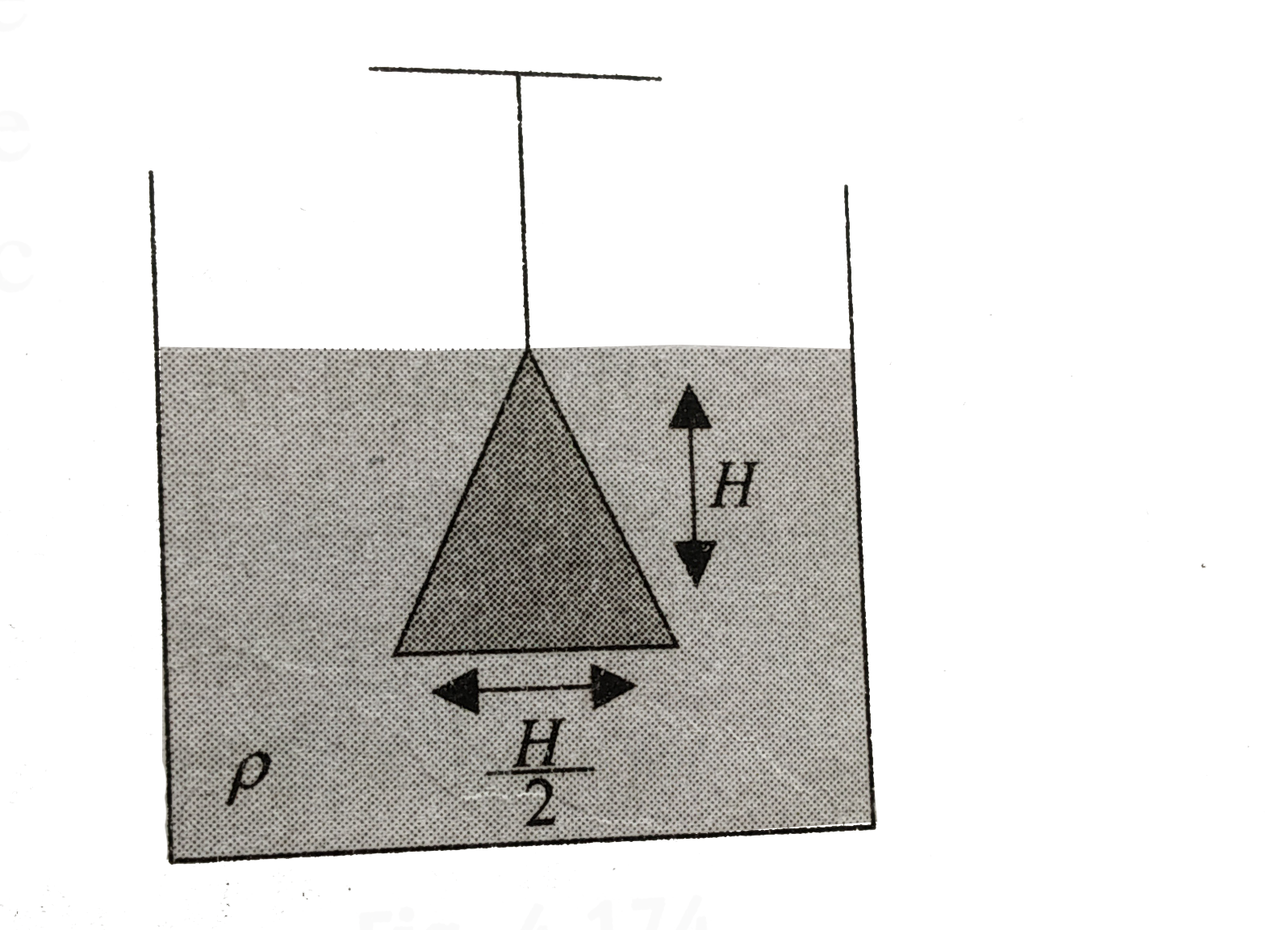
πH2(P04+ρgH3)
πH2(P04+ρgH6)
πH24(P04+ρgH)
πH24(P0+ρgH)
The correct Answer is:B
13π(H2)2Hρg=(P0+ρgH)π(H2)2−Fv
Fv=P0πH24+ρg(H3)4π−πH3ρg12
=P0πH24+ρgH3π6
Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water).
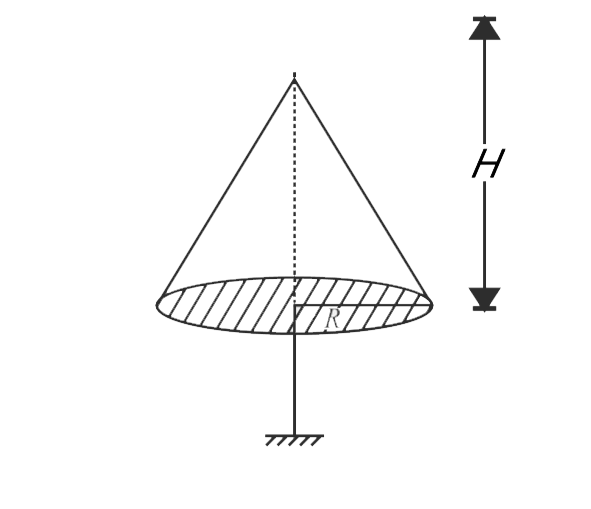
(a) Find tension in the string.
(b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p0.
View SolutionThe radius of the base of a cone is 14 cm and its height is 48 cm . What is the curved surface area of the cone ?
View Solution
Knowledge Check
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
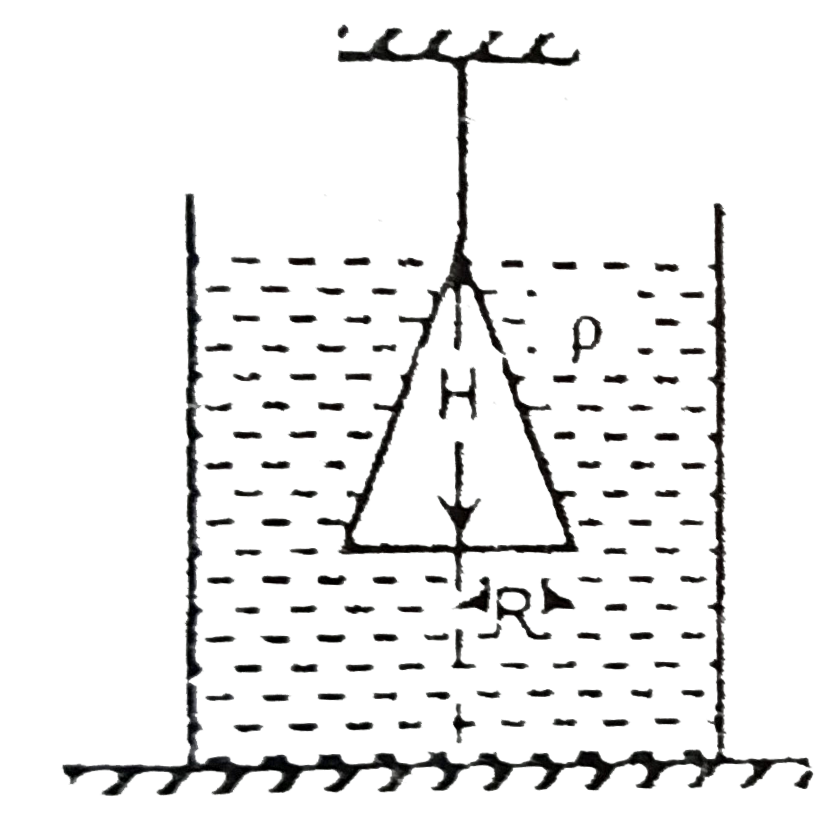 AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)Aπr2dg(H−r3)B2πr2dg(H−2r3)Cπr2dg(2H−r3)Dπr2dg(2H−2r3)The area of the base of a right circular cone is 154 cm2 and its height is 14cm . Its curved surface area is
A(154×√5)cm2B11cm2C(154+√7)cm2D5324cm2
A solid cone of height 8 cm and base radius 6 cm is melted and recast into identical cones, each of height 2 cm and radius 1 cm. What is the number of cones formed ?
View SolutionFind the curved surface area of a cone whose height is 12cm and base radius is 5cm ?
View SolutionA charge q is placed at a height h4 from the base of a cone of height h and radius R as shown in figure. Calculate the flux linked with the curved surface of the cone.
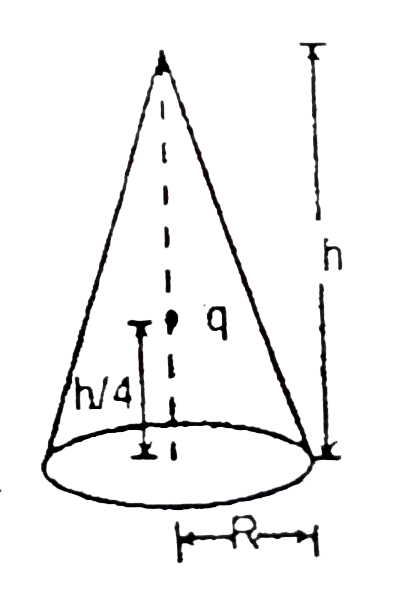
View SolutionThe cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.

View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View Solution

