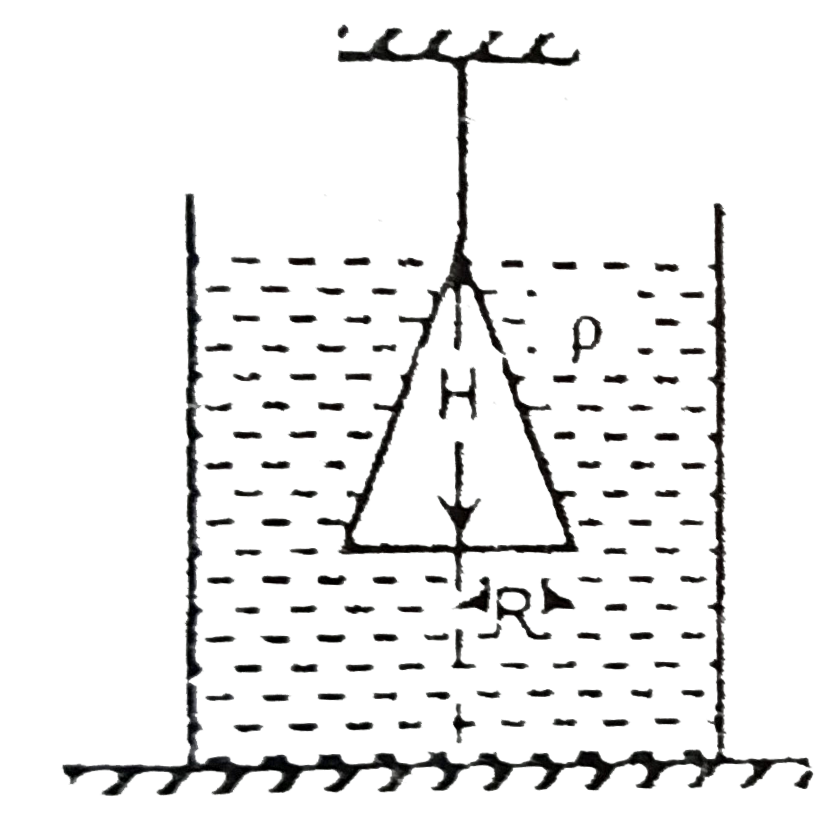
The cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.

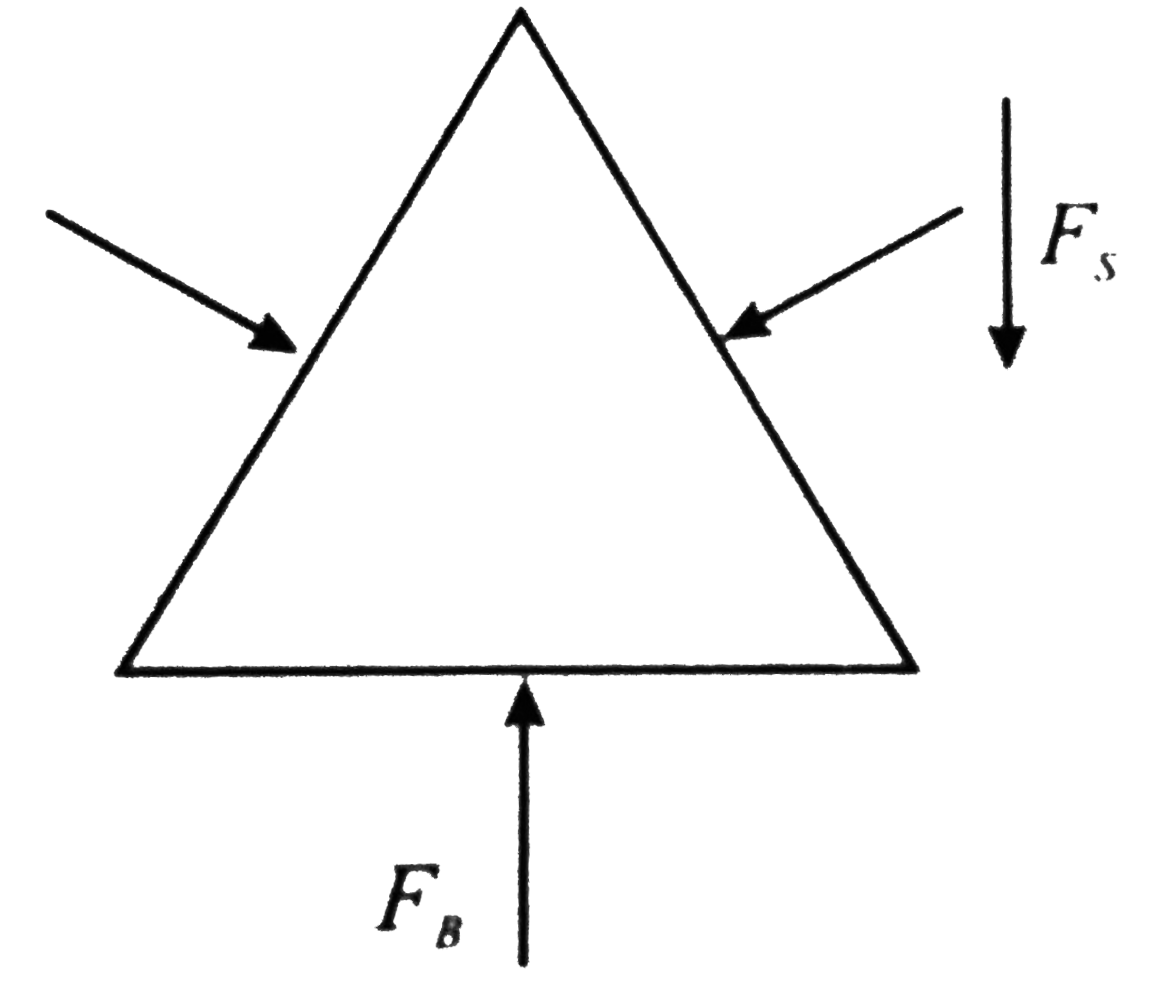
Net force on the cone by the liquid is equal to buoyancy force on the cone.
Force on the bottom surfae of the cone is more than buoyancy force on the cone.
Net force on the slant surface of the cone is more than buoyancy force on the cone.
Net force on the slant surface of the cone is less than buoyancy force on the cone.
The correct Answer is:A, B, C
B=FB−FS, where FS is the net vertical downward force on the slant surface and FB is net force on the bottom surface.
B=Vρg=13πR2ρg,FB=ρgHπR2
Now Fs=Fb−B
⇒FS=ρgHπR2−HρgπR23=23ρgHπR2
Clearly FB>B,FS>B
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:LC_TYPE
Explore 34 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- MISCELLANEOUS VOLUME 2Book:CENGAGE PHYSICSChapter:MISCELLANEOUS VOLUME 2Exercise:INTEGER_TYPE
Explore 10 Videos
- MISCELLANEOUS KINEMATICSBook:CENGAGE PHYSICSChapter:MISCELLANEOUS KINEMATICSExercise:Interger type
Explore 3 Videos
- NEWTON'S LAWS OF MOTION 1Book:CENGAGE PHYSICSChapter:NEWTON'S LAWS OF MOTION 1Exercise:Integer
Explore 5 Videos
Similar Questions
Knowledge Check
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
 AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
AρπgHR2BπρgHR2C43πρgHR2D23πρgHR2
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)Aπr2dg(H−r3)B2πr2dg(H−2r3)Cπr2dg(2H−r3)Dπr2dg(2H−2r3)A sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
A(ρ2−σρ1−σ)v1B(ρ1−σρ1−σ)v1C(ρ1ρ2)v1D(ρ2ρ1)v1
A right circular cone with radius R and height H contains a liquid which evaporates at a rate proportional to its surface area in contact with air (proportionality constant k is positive). Suppose that r(t) is the radius of the liquid cone at time t. The radius of water cone at t = 1 is
View SolutionA right circular cone with radius R and height H contains a liquid which evaporates at a rate proportional to its surface area in contact with air (proportionality constant k is positive). Suppose that r(t) is the radius of the liquid cone at time t. The time after which the cone is empty is
View SolutionFrom a uniform solid cone of base radius R and height H, a symmetric cone of the base radius R2 is removed as shown. Then the centre of mass is shifted by H/n. Find the value of of n.
View SolutionWhen one end of a tube of radius r is immersed vertically in a liquid of density ρ, surface tension S, the rise of liquid in the tube is h and angle of contact is θ . If the tube is broken and its length is made h'(<h), then find the value of height of rise of liquid in the tube and angle of contact.
View SolutionA cylindrical vessel of base radius R and height H has a narrow neck of height h and radius r at one end (see figure). The vessel is filled with water (densityρw) and its neck is filled with immiscible oil (density ρO). Then the pressure at
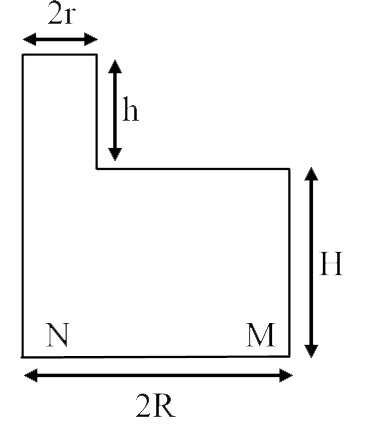
View Solution