The minimum horizontal acceleration of the container4 so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
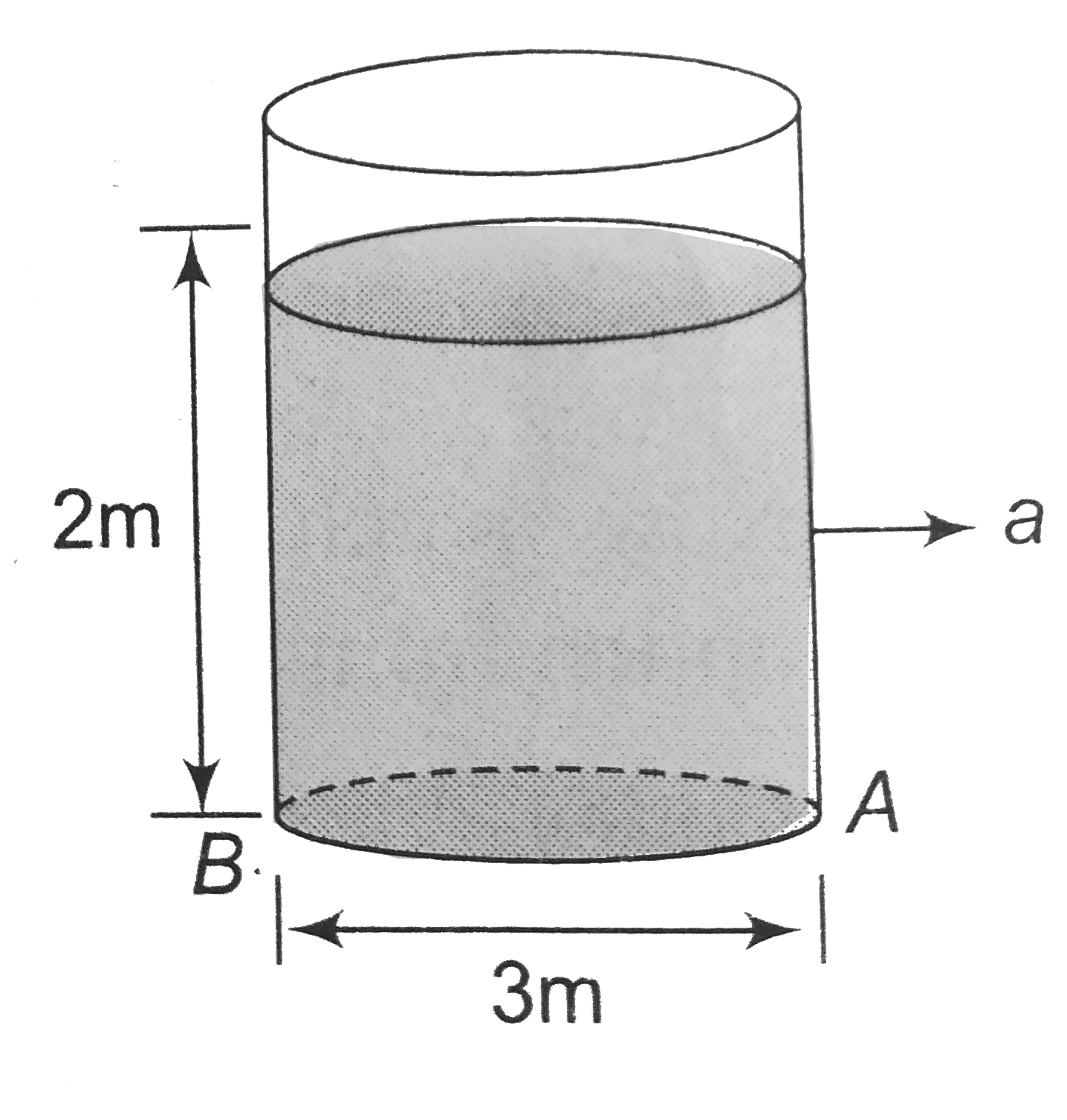
32g
43g
42g
34g
The correct Answer is:B
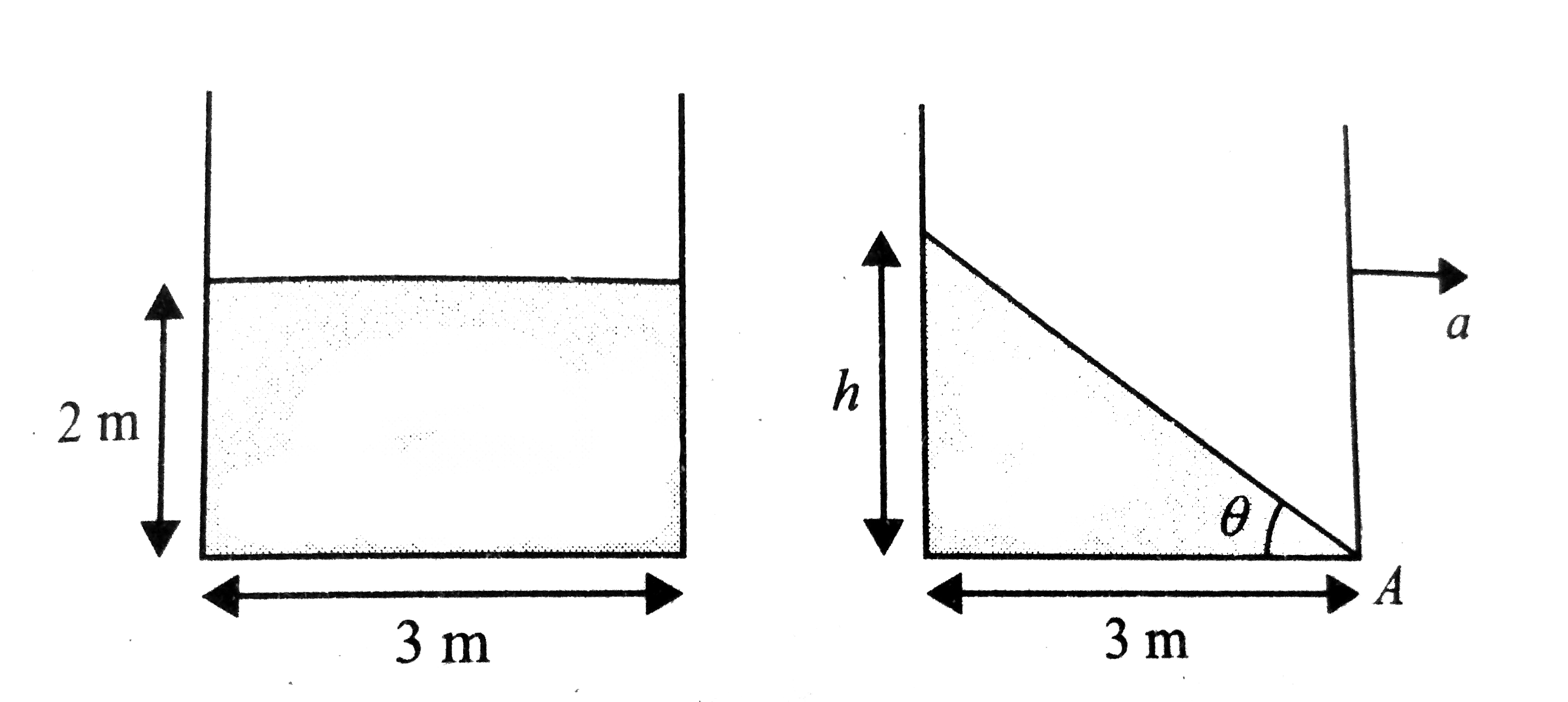
Volume equality gives
2×3=12×h×3⇒h=4m
∴tanθ=43=ag⇒a=43g
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Assertion-Reasoning
8 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Subjective
25 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Videos
Similar Questions
Knowledge Check
The minimum horizontal acceleration of the container IS a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
 A32gB43gC42gD34g
A32gB43gC42gD34gThe pressure at the bottom of a tank containing a liquid does not depend on
AAcceleration due to gravityBHeight of the liquid columnCArea of the bottom surfaceDNature of the liquidThe pressure at the bottom of a tank containing a liquid does not depend on
AAcceleration due to gravityBHeight of the liquid columnCArea of the bottom surfaceDNature of the liquid
Prove that the pressure exerted by water at the bottom of the container depends on the height of its column.
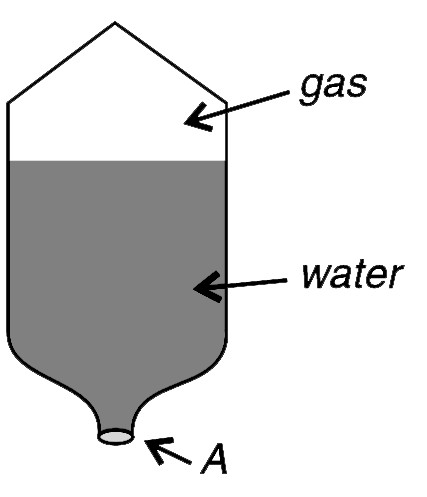
View SolutionTo illustrate th principle of a rocket, a student designed a water rocket as shwon in the figure. It is basically a container having pressurized gas in its upper part and water in its lower part. Pressure of the gas is 4.0Mpa. Mass of empty container is 1.0kg and mass of its content is also 1.0kg. The nozzle at the bottom is opened to impart a vertical acceleration to the contaienr. If it is desired that the initial upwards acceleration of the container be 0.5g. what should be the cross sectional area (A) of the exit of the nozzle?
Neglect the pressure due to height of water in the contaienr and take atmospheric pressure to be 1.0MPa. g=10ms−2.
View SolutionIf the container filled with liquid gets accelerated horizontally or vertically, pressure in liquid gets changed. In liquid (ay) for calculation of pressure, effective g is used. A closed box horizontal base 6m by 6m and a height 2m is half filled with liquid. It is given a constant horizontal acceleration g/2 and vertical downward acceleration g/2.
Water pressure at the bottomof centre of the box is equal to (atmospheric pressure =105N/m2 density of water =1000kg/m3,g=10m/s2)
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

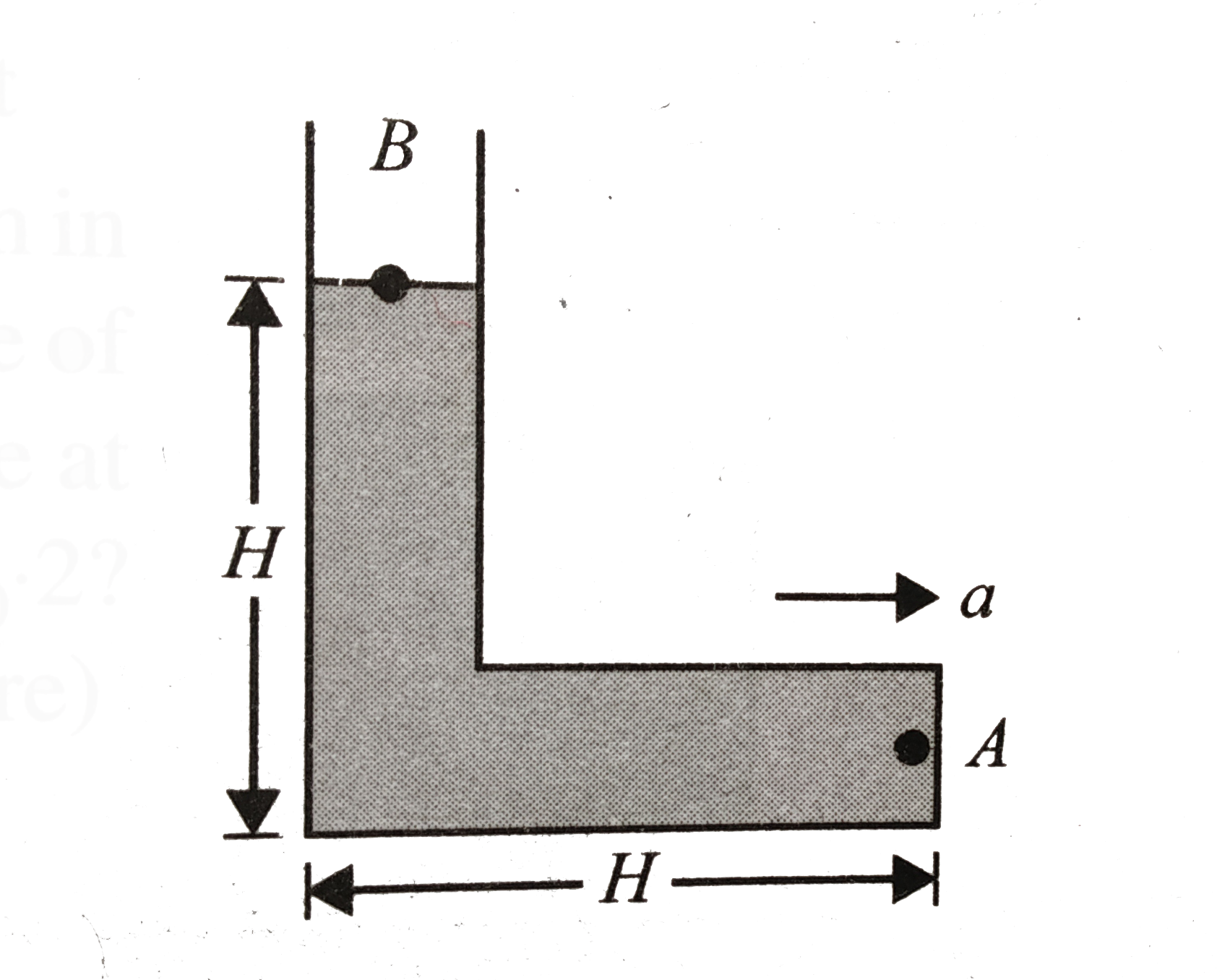
View SolutionFor the L-shaped vessel shown in the figure, determine the value of acceleration a so that pressure at point A becomes equal to p02? (p0 is the atmospheric pressure)
View Solution

