A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is

ρ2ρ1
ρ2−ρρ2−ρ1
ρ−ρ1ρ2−ρ1
ρ1ρ2
The correct Answer is:B
Let V be the total volume of the ball and v be the volume of the ball in the upper liquid. Then V−v is the volume of the lower liquid displaced.
Using the law of floatation we have
Vρg=vρ1+(V−v)ρ2g
Vρ=vρ1+Vρ2−vρ2
or V(ρ−ρ2)=v(ρ1−ρ2)
vV=ρ−ρ2ρ1−ρ2=ρ2−ρρ2−ρ1

Topper's Solved these Questions
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Multipe Correct
Explore 15 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Assertion-Reasoning
Explore 8 Videos
- FLUID MECHANICSBook:CENGAGE PHYSICSChapter:FLUID MECHANICSExercise:Subjective
Explore 25 Videos
- DIMENSIONS & MEASUREMENTBook:CENGAGE PHYSICSChapter:DIMENSIONS & MEASUREMENTExercise:Integer
Explore 2 Videos
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:INTEGER_TYPE
Explore 1 Video
Similar Questions
A stream line body with relative density ρ1 falls into air from a height h1 on the surface of a liquid of realtive density ρ2, where ρ2>ρ1. Find the time of immersion of the body into the liquid.
View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View Solution
Knowledge Check
A Solid uniform ball of volume V floats on the interface of two immiscible liquids . [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is the specific gravity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
A23VB13VCV4D3V4A solid uniform ball of volume V floats on the interface of two immiscible liquids [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is th especific gracity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
A23VB13VCV4D3V4A solid uniform ball having volume V and density ρ floats at the interface of two unmixable liquids as shown in the figure. The densities of the upper and the lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2 . What fraction of the volume of the ball will be in the lower liquid ?
 Aρ−ρ2ρ1−ρ2Bρρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2
Aρ−ρ2ρ1−ρ2Bρρ1−ρ2Cρ1−ρρ1−ρ2Dρ1−ρ2ρ2
A solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densityes ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionA uniform cube of mass M is floating on the surface of a liquid with three fourth of its volume immersed in the liquid (density=ρ). The length of the side of the cube is equal to

View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
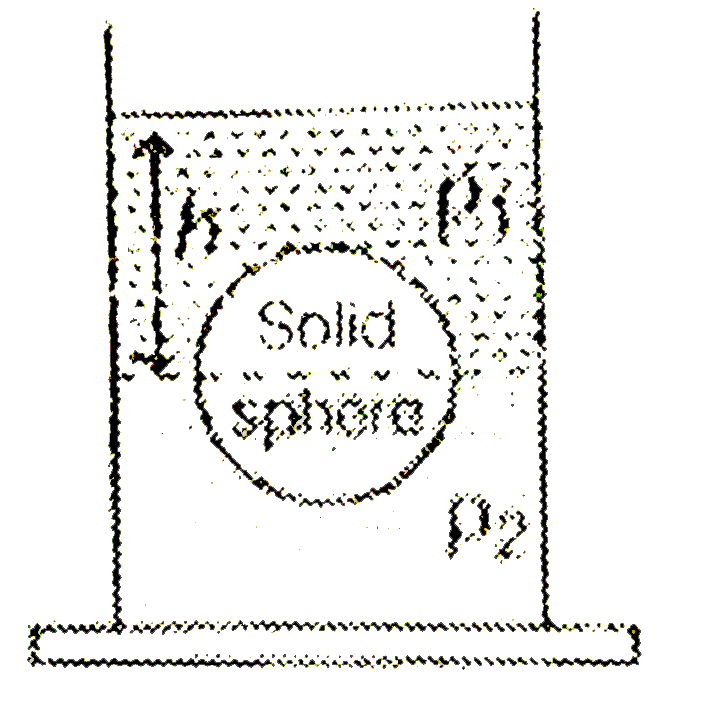
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View Solution

