
Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.
The coefficient of viscosity varies as η=η0x (x measured from centre of the disk) at the given instant the disk is floating towards right with a velocity v as shown, find the force required to move the disk slowly at the given instant.
2η0R2vT
8η0R2vT
πη0R2vT
16η0R3vT
The correct Answer is:C
df=ηAdvdx
f=∫R0(η0x).(2πxdx)VT
f=23.πη0R3VT
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Single Answer Questions
Explore 108 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:integer Type Questions
Explore 25 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:Comprehension Type Questions
Explore 40 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBook:NARAYNAChapter:MATHEMATICAL REVIEW & PHYSICAL WORLDExercise:C.U.Q
Explore 13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:NARAYNAChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:LEVEL-II (H.W)
Explore 24 Videos
Similar Questions
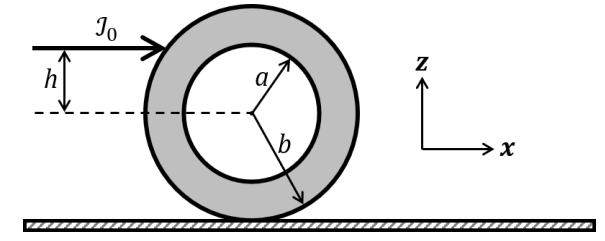
An annular disk of mass M, inner radius a and outer radius b is placed on a horizontal surface with coefficient of friction μ,as shown in the figure. At some time, an impulse J0ˆx is applied at a height h above the center of the disk. If h = hm then the disk rolls without slipping along the x-axis. Which of the following statement(s) is (are) correct?
View SolutionA metal plate of area 10−3m2 is placed on a liquid layer of thickness 0.8mm . The coefficient of viscosity of that liquid is 24poise.Then the horizontal force required to move the plate with a velocity of 1cms−1.
View Solution
Knowledge Check

Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.

The torque required to rotate the disk at a constant angular velocity Ω given the viscosity is uniformly η.A4πωηR4TBπωηR42TC2πωηR4TD16πωηR4
Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.
A disc rotating with angularvelocity ω is placed on a viscous liquid of thickness T. Find the angle rotated by the disc before it comes to rest. (viscosity=η, mass of disc =M, radius of disc =R)A4ω0TMηπR2B2ω0TMηπR2Cω0TMηπR2Dω0TM2ηπR2A sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time v0>ω0R)
 Av0/μgBω0R/μgC2(v0−ω0R)/5μgD2(v0−ω0R)/7μg
Av0/μgBω0R/μgC2(v0−ω0R)/5μgD2(v0−ω0R)/7μg
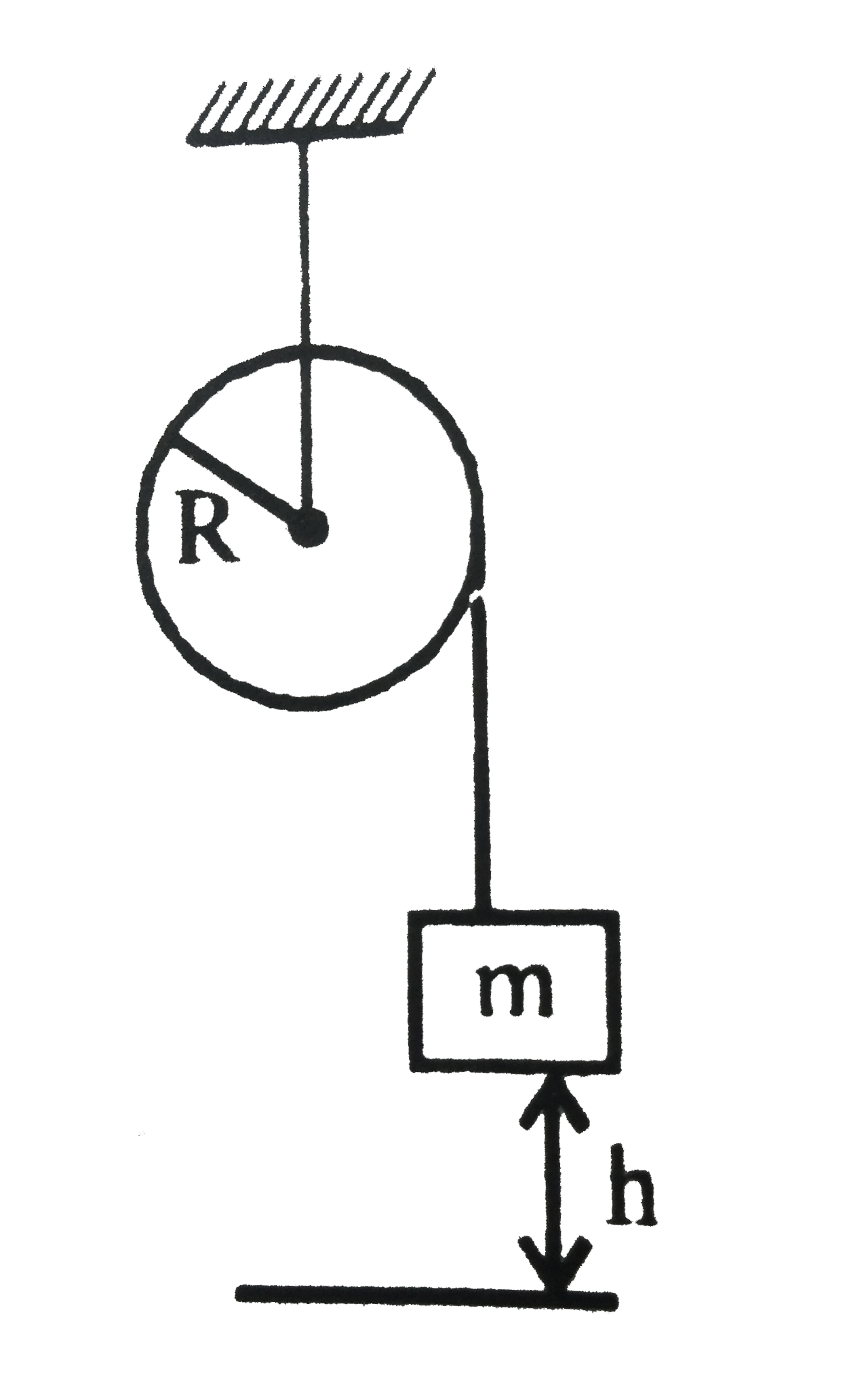
A mass m is attached to a pulley through a cord as shown in figure. The pulley is a solid disk with radius R. The cord does not slip on the disk. The mass is released from rest at a height h from the ground and at the instant the mass reaches the ground, the disk is rotating with angular velocity ω. Find the mass of the disk.
 .
.
View SolutionA liquid of coefficient of viscosity η is flowing steadily through a capillary tube of radius r and length I. If V is volume of liquid flowing per sec. the pressure difference P at the end of tube is given by
View SolutionA small steel ball of mass m and radius r is falling under gravity through a viscous liquid of coefficient of viscosity η. If g is the value of acceleration due to gravity. Then the terminal velocity of the ball is proportional to (ignore buoyancy)
View SolutionThe terminal velocity v of a small steel ball ofradius r fal ling under gravity through a column ofa viscous liquid of coefficient of viscosity η depends on mass of the ball m, acceleration due to gravity g, coefficient of viscosity η and radius r. Which of the following relations is dimensionally correct?
View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.

The maximum value of V0 for whic the disk will roll without slipping is-
View Solution

