
Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.
A disc rotating with angularvelocity ω is placed on a viscous liquid of thickness T. Find the angle rotated by the disc before it comes to rest. (viscosity=η, mass of disc =M, radius of disc =R)
4ω0TMηπR2
2ω0TMηπR2
ω0TMηπR2
ω0TM2ηπR2
The correct Answer is:C
τ=πωηR42T=Iα=MR22α and α=ω.dωdthη
∵θ=ωTMηπR2
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Single Answer Questions
108 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - integer Type Questions
25 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - Comprehension Type Questions
40 Videos
- MATHEMATICAL REVIEW & PHYSICAL WORLDBOOK - NARAYNACHAPTER - MATHEMATICAL REVIEW & PHYSICAL WORLDEXERCISE - C.U.Q
13 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
Similar Questions
A disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionSelect ALL correct answer :
A disc of radius R is placed over a horizontal table in such a way that plane of the disc is horizontal and rotated about its vertical axis passing through its center with angular velocity ω. A layer of grease of thickness l is present between the table and the disc.Coefficient of viscosity of grease is η .Then,
(A) torque needed to rotate the disc with constant angular velocity is πηωR44l
(B) torque needed to rotate the disc with constant angular velocity is πηωR42l
(C) power needed to rotate the disc with constant angular velocity is πηω2R42l
(D) power needed to rotate the disc with constant angular velocity is πnω2R44l
View Solution
Knowledge Check

Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.

The torque required to rotate the disk at a constant angular velocity Ω given the viscosity is uniformly η.A4πωηR4TBπωηR42TC2πωηR4TD16πωηR4
Consider a disk of mass m, radius R lying on a liquid layer of thickness T and coefficient of viscosity η as shown in the fig.
The coefficient of viscosity varies as η=η0x (x measured from centre of the disk) at the given instant the disk is floating towards right with a velocity v as shown, find the force required to move the disk slowly at the given instant.A2η0R2vTB8η0R2vTCπη0R2vTD16η0R3vTA point mass m collides with a disc of mass m and radius R resting on a rough horizontal surface as shown . Its collision is perfectly elastic. Find angular velocity of the disc after pure rolling starts
 A(2u3R)B(3u3R)C(5u3R)D(2u5R)
A(2u3R)B(3u3R)C(5u3R)D(2u5R)
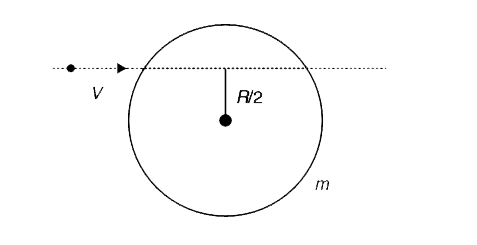
A disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
View SolutionA disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionA disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
View SolutionA disc has mass 'M" and radius 'R'. How much tangential force should be applied to the rim of the disc so as to rotate with angular velocity ω in time 't'?
View SolutionA disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time 't' ?
View Solution
