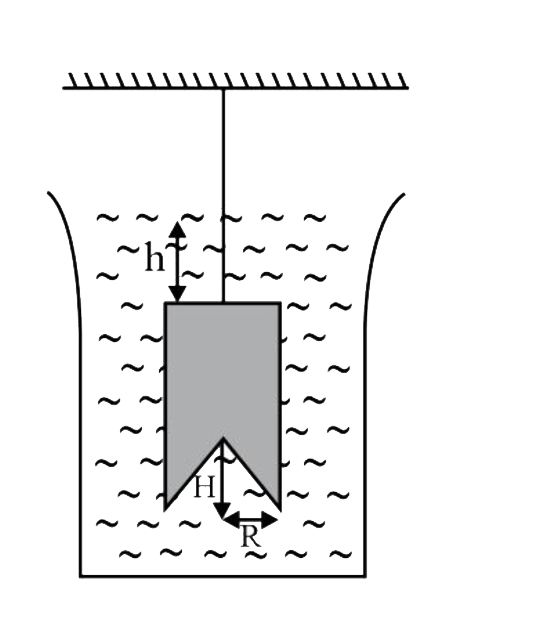
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
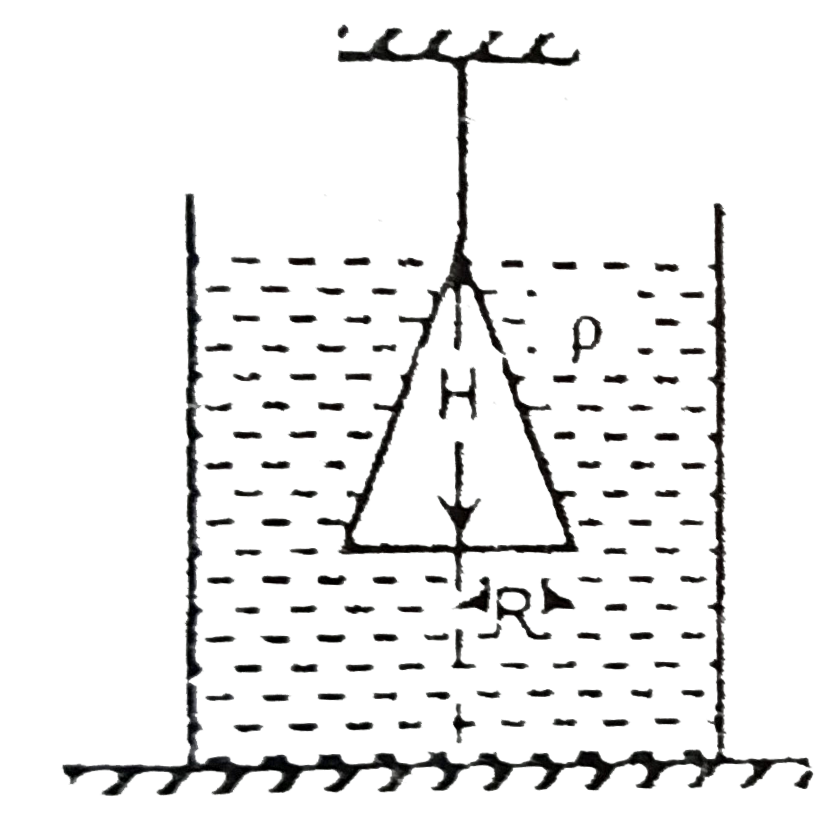
ρπgHR2
πρgHR2
43πρgHR2
23πρgHR2
HρgπR2−Fa=FB
FB=Vρg=13πR2Hρg
∴F3=HρgπR2−HρgπR23=23πR2ρGh
Topper's Solved these Questions
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Assertion & Reason
Explore 15 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Multiple Question
Explore 58 Videos
- GMP ASSESMENTBook:FIITJEEChapter:GMP ASSESMENTExercise:Numerical Based
Explore 61 Videos
- GENERAL PHYSICSBook:FIITJEEChapter:GENERAL PHYSICSExercise:MATRIX MATCH TYPE
Explore 3 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
Similar Questions
Consider a regular tank of size (l×b) filled with a liquid of density ρ to a height H as shown in figure. Find the force at the base and on the wall of the tank.

View SolutionWhen a capillary tube of radius r is immersed in a liquid of density ρ, the liquid rises to a height h in it. If m is the mass of the liquid in the capillary tube, find the potential energy of this mass of the liquid in the tube.
View Solution
Knowledge Check
The cone of radius R and height H is hanging inside a liquid of density by means of a string a shwon in the figure.
 ANet force on the cone by the liquid is equal to buoyancy force on the cone.BForce on the bottom surfae of the cone is more than buoyancy force on the cone.CNet force on the slant surface of the cone is more than buoyancy force on the cone.DNet force on the slant surface of the cone is less than buoyancy force on the cone.
ANet force on the cone by the liquid is equal to buoyancy force on the cone.BForce on the bottom surfae of the cone is more than buoyancy force on the cone.CNet force on the slant surface of the cone is more than buoyancy force on the cone.DNet force on the slant surface of the cone is less than buoyancy force on the cone.A solid cone of height H and base radius H2 floats in a liquid of density ρ. It is hanging from the ceiling with the help of a string. The force by the fluid on the curved surface of the cone is (P0= atmospheric pressure)
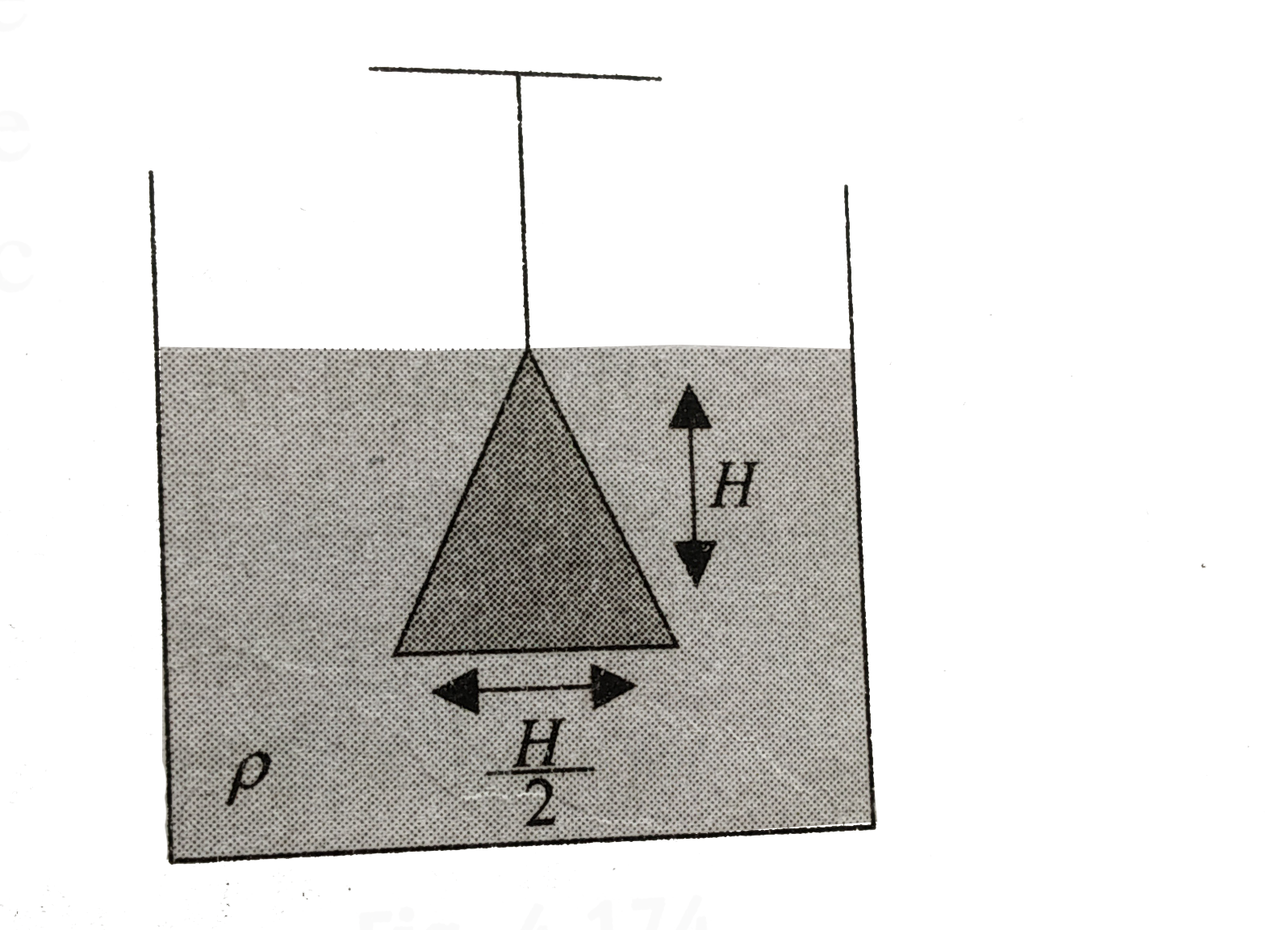 AπH2(P04+ρgH3)BπH2(P04+ρgH6)CπH24(P04+ρgH)DπH24(P0+ρgH)
AπH2(P04+ρgH3)BπH2(P04+ρgH6)CπH24(P04+ρgH)DπH24(P0+ρgH)A beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
AhρgBhρ(g+a)Chρ(g−a)D2hρg(g−ag+a)
A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is v. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water).
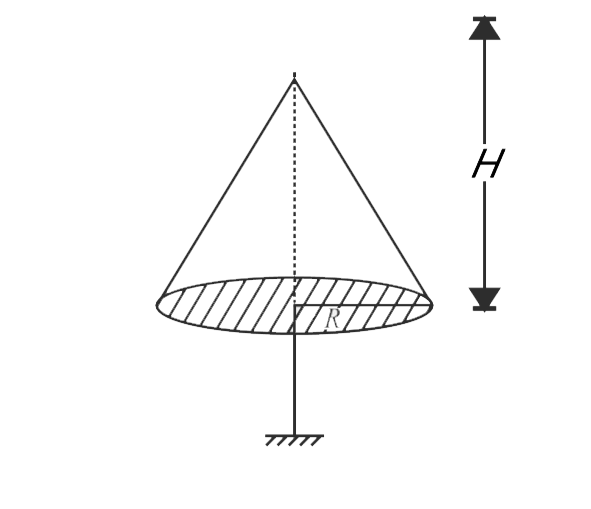
(a) Find tension in the string.
(b) Find the force applied by the water on the slant surface of the coone. take atmospheric pressure to be p0.
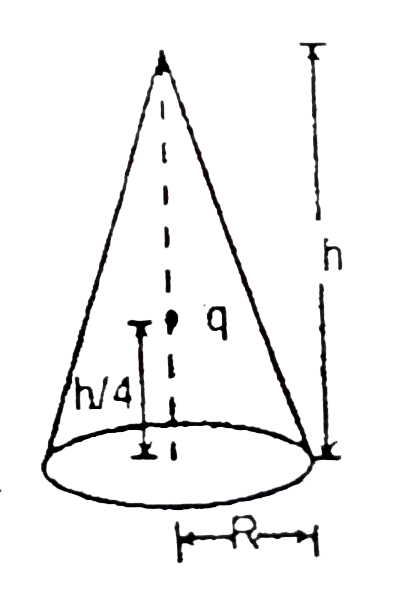
View SolutionA charge q is placed at a height h4 from the base of a cone of height h and radius R as shown in figure. Calculate the flux linked with the curved surface of the cone.
View Solution
A cone of radius r and height r is under a liquid of density d.its base is parallel to the free surface of the liquid at a depth H from it as shown.What is the net force due to liquid on its curved surface? (neglect atmospheric pressure)
View SolutionA triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is
View Solution

