Two identical rods of length , area of cross-sectional and thermal conductivity are joined end to end. If temperature difference of free ends is , the heat flows along rods per second. Find the total heat flowing per second along the rods if the two rods are placed parallel and temperature difference of free ends is . There is no heat loss from curved surface.
For series connection
For parallel connection
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason15videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Multiple Question58videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Numerical Based61videos
GMP ASSESMENT
- BOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE3videos
GENERAL PHYSICS
- BOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question2videos
GRAVITATION
Similar Questions
Three rods of same cross-section but different length and conductivity are joined in series . If the temperature of the two extreme ends are T1andT2(T1>T2) find the rate of heat transfer H.
 View Solution
View SolutionTwo identical rods AB and CD, each of length L are connected as shown in figure-4.22. Their cross-sectional area is A and their thermal conductivity is k. Ends A, C and D are maintained at temperatures T1,T2andT3 respectively. Neglecting heat loss to the surroundings, find the temperature at B.
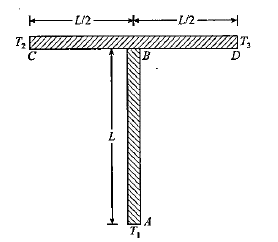 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The lengths and radii of two rods made of same material are in the ratios 1 : 2 and 2 : 3 respectively. If the temperature difference between the ends for the two rods be the same, then in the steady state, the amount of heat flowing per second through them will be in the ratio
A1:3B4:3C8:9D3:2 - Question 2 - Select One
The lengths and radii of two rods made of same material are in the ratios 1 : 2 and 2 : 3 respectively. If the temperature difference between the ends for the two rods be the same, then in the steady state, the amount of heat flowing per second through them will be in the ratio
A1:3B4:3C8:9D3:2 - Question 3 - Select One
Two adiabatic vessels, each containing the same mass m of water but at different temperatures, are connected by a rod of length L, cross-section A, and thermal conductivity K. the ends of the rod are inserted into the vessels, while the rest of the rod is insulated so that .there is negligible loss of heat into the atmosphere. The specific heat capacity of water is s, while that of the rod is negligible. The temperature difference between the two vessels reduces to l/e of its original value after a time, δt. The thermal conductivity (K) of the rod may be expressed by:
AmsLAδtBemsLAδtCmsL2eAδtDmsL2Aδt
Figure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section. A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat top the atmosphere.
 View Solution
View SolutionTwo rods of same length and cross section are joined along the length. Thermal conductivities of first and second rod are K1 and K2. The temperature of the free ends of the first and seconds rods are maintained at θ1 and θ2 respectively. The temperature of the common junction is
View SolutionThe ends of the two rods of different materials with their lengths, diameters of cross-section and thermal conductivities all in the ratio 1 : 2 are maintained at the same temperature difference. The rate of flow of heat in the shorter rod is 1cals−1. What is the rate of flow of heat in the larger rod:
View SolutionTwo rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
View SolutionTwo rods of the same length and areas of cross-section A1 and A2 have their ends at the same temperature. K1 and K2 are the thermal conductivities of the two rods. The rate of flow of heat is same in both the rods if-
View Solution

