Question

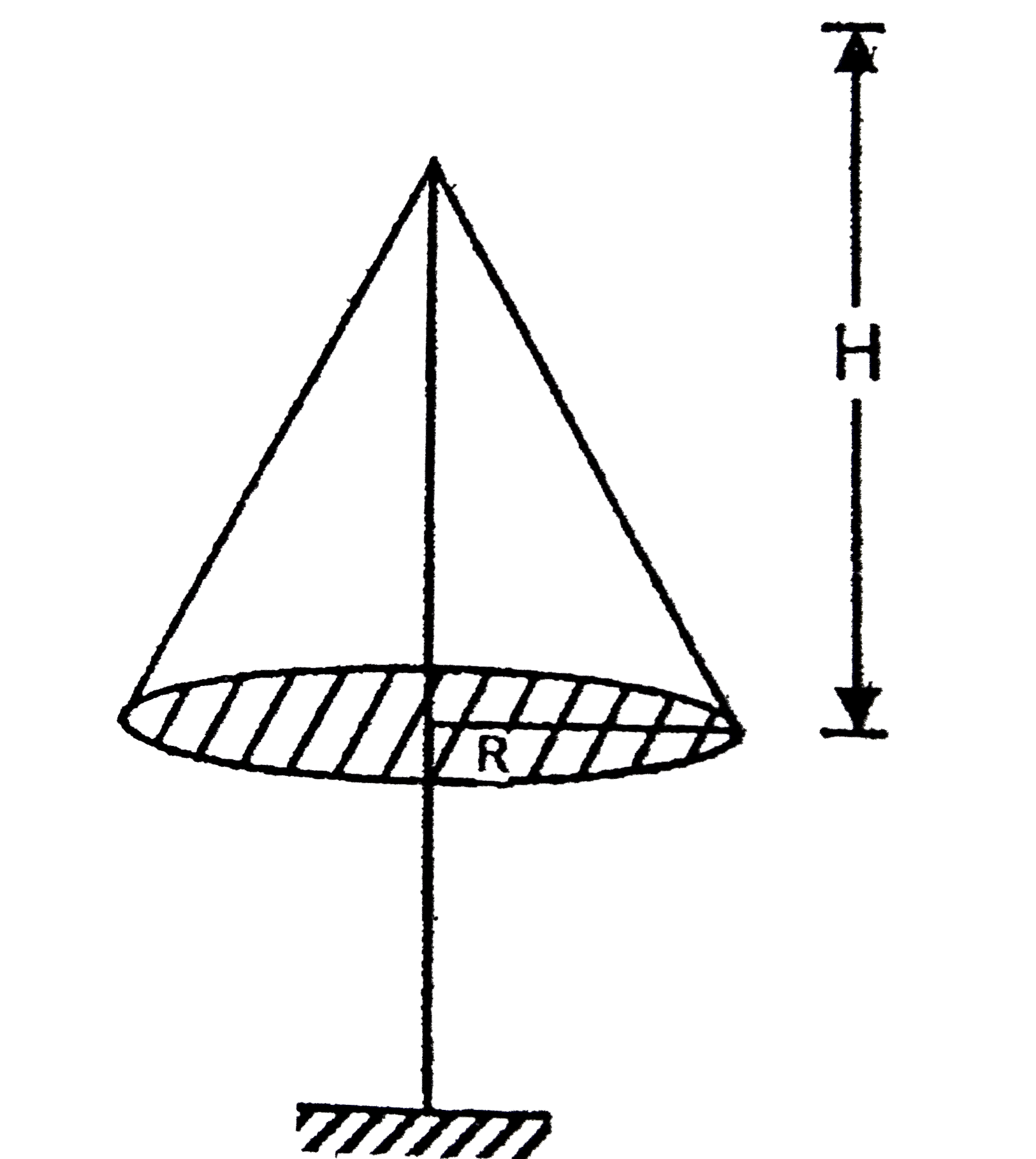
A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is $R$ and the volume of the cone is $V$. In equilibrium the base of the cone is at a depth $H$ below the water surface. Density of wood is $d(<\rho$, density of water) Then tension in the string is

Options

A. `Vg(rho -d)`
B. `Vg(d+rho)`
C. `2Vg(rho - d)`
D. None of these

Answer

A

Explanation

(a) Buoyancy force is `F_(B) = vrhog`
Weight of the cone `W = vdg`
`:.` Tension `T = W - F_(a) = vg(d- rho)`
(b) `F_(B) - vrhog`
Buoyancy is resultant of vertically upward force `(F_(1))` applied by water perssure on the base of the cone
and the vertically downward force `(F_(2))` applied by water on the slant surface. [The horizontal component of this force same up to zero due to symmetry

`:. F_(1) - F_(2) = F_(B)`
`piR^(2) .[rho_(0) + rhogH] - F_(2) = vrhog`
`:. F_(2) = piR^(2)[rho_(0) + rhogH] - vrhog`