A beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
hρg
hρ(g+a)
hρ(g−a)
2hρg
The correct Answer is:B
To solve the problem of finding the pressure due to a liquid at a depth h below the free surface when the beaker is moving upwards with an acceleration a, we can follow these steps:
1. Understand the Basic Concept of Pressure in Fluids:
The pressure at a certain depth h in a fluid at rest is given by the formula:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the depth below the free surface.
2. Consider the Effect of Acceleration:
When the beaker is accelerating upwards with an acceleration a, we need to consider the effect of this acceleration on the pressure at depth h. In this case, we introduce a pseudo force acting downwards due to the upward acceleration of the beaker.
3. Combine the Effects of Gravity and Acceleration:
The effective acceleration acting on the liquid at depth h will be the sum of the gravitational acceleration g and the upward acceleration a. Therefore, the total effective acceleration acting downwards is:
g+a
4. Write the Modified Pressure Formula:
Now, substituting the effective acceleration into the pressure formula, we get:
P=ρ(g+a)h
5. Final Expression for Pressure:
Thus, the pressure at a depth h below the free surface of the liquid in the moving beaker is:
P=ρh(g+a)
Final Answer:
The pressure due to the liquid at a depth h below the free surface of the liquid is given by:
P=ρh(g+a)
The pressure at a certain depth h in a fluid at rest is given by the formula:
P=ρgh
where ρ is the density of the liquid, g is the acceleration due to gravity, and h is the depth below the free surface.
When the beaker is accelerating upwards with an acceleration a, we need to consider the effect of this acceleration on the pressure at depth h. In this case, we introduce a pseudo force acting downwards due to the upward acceleration of the beaker.
The effective acceleration acting on the liquid at depth h will be the sum of the gravitational acceleration g and the upward acceleration a. Therefore, the total effective acceleration acting downwards is:
g+a
Now, substituting the effective acceleration into the pressure formula, we get:
P=ρ(g+a)h
Thus, the pressure at a depth h below the free surface of the liquid in the moving beaker is:
P=ρh(g+a)
The pressure due to the liquid at a depth h below the free surface of the liquid is given by:
P=ρh(g+a)
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL -2
Explore 50 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL-0 ( Short Answer Type - II )
Explore 15 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
View SolutionA conical portion of radius R and height H is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at depth h below the liquid surface . The force on the bottom of the cylinder by the liquid is

View Solution
Knowledge Check
A hemispherical portion of a radius R is removed from the bottom of a cylinder of radius R. The volume of the remaining cylinder is V and its mass is M. It is suspended by a string in a liquid of density ρ where it stays vertical . The upper surface of the cylinder is at a depth of h below the liquid surface. THe force on the bottom of the cylinder by the liquid is
AM gBMg−Vρ gCMg+ΠR2hgρDρg(V+ΠR2h)The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρThe pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth
A cone of radius R and height H, is hanging inside a liquid of density ρ by means of a string as shown in figure. The force due to the liquid acting on the slant surface of the cone is
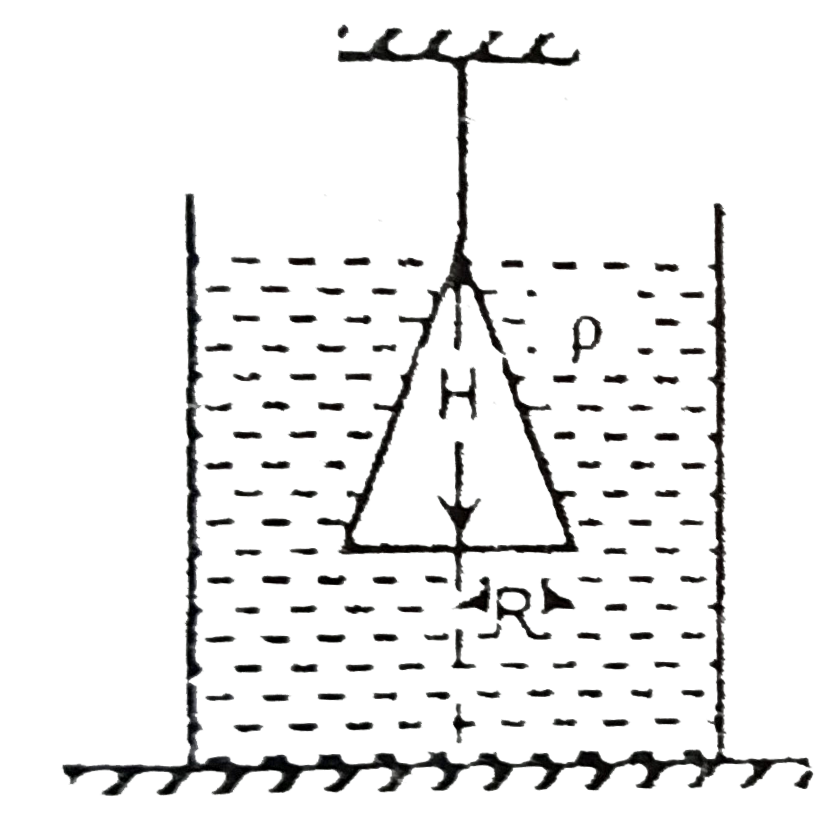
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionA sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be

View Solution_E01_052_Q01.png)
An object of volume V is submerged in a liquid of density ρ. It has flat bottom of area A which is at depth of H in the liquid and a dome shaped top find the total force of liquid acting on the top of the object.
View SolutionA container containing a liquid is moving down an incline plane with constant acceleration 'a' . The angle made by the water surface in equilibrium with the inclined plane is

View Solution
