A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B is
hρg
Lρa
hρg−Lρa
hρg+Lρa
The correct Answer is:D
PC−PA=ρaL also PB−PC=ρghorPB−(PA+ρaL)ρghorPB−PA=hρg+ρLa
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL -1
Explore 90 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions
Knowledge Check
The pressure inside a liquid of density ρ at a depth h is :
AhρgBhρgChρgDhρ
Figure shows a siphon. The liquid shown in water. The pressure difference PB−PA between the points A and B is

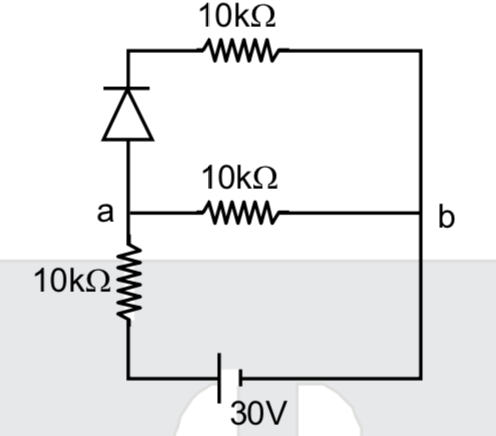
View SolutionA liquid kept in a container has a horizontal acceleration 'a' as shown in figure.
Using the pressure equation along the path ABC find the angle θ.
View SolutionIn the circuit shown in figure potential difference between the points A and B in the steady state is
View SolutionA beaker containing a liquid of density ρ moves up with an acceleration a. The pressure due to the liquid at a depth h below the free surface of the liquid is.
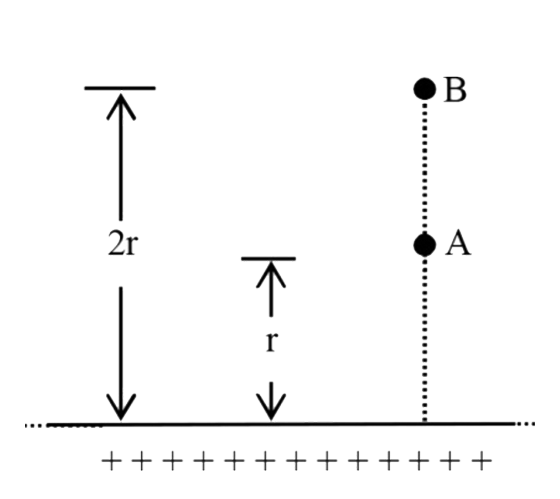
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
View SolutionFigure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.

View SolutionA ball of density ais released from rest from the centre of an accelerating sealed cubical vessel completely filled with a liquid of density ρ. If the trough moves with a horizontal acceleration →a0 find the initial acceleration of the ball.
View Solution