The tension in a string holding a solid block below the surface of a liquid (of density greater than that of solid) as shown in figure is T0 when the system is at rest. What will be the tension in the string if the system has an upward acceleration a?
 .
.
T(1−ag)
T(1+ag)
T(ag−1)
agT
The correct Answer is:B
When system is at rest:
T=B−mg=Vρ1g−(Vpg)=V(ρ1−ρ)g ...(i)
Where ρ1 = Density of liquid and ρ = Density of block
If system is moving upward with acceleration a: B'−mg−T'=ma⇒Vρ1(g+a)−Vρ(g+a)=T'
T'=V(ρ1−ρ)(g+a) ...(ii) From (i) and (ii) T'=T(1+ag)
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -1
90 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
For the system shown in figure, the tensions in the string
View SolutionThe tension T in the string shown in figure is

View SolutionA string is holding a solid block below the surface of the liquid as shown in figure. If the system is given an upward acceleration a, then as compared to previous state.

View SolutionA string is holding a solid block below the surface of the liquid as shown in figure. If the system is given an upward acceleration a, then as compared to previous state.

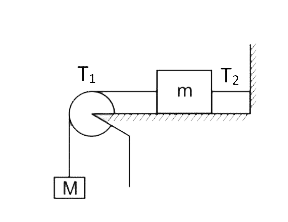
View SolutionFind the tension T2 in the system shown in the figure.
View SolutionConsider the double Atwood's machine as shown in the figure
(a) Whatis acceleration of the masses?
(b) What is the tension in each string?

View SolutionConsider the double Atwood's machine as shown in the figure
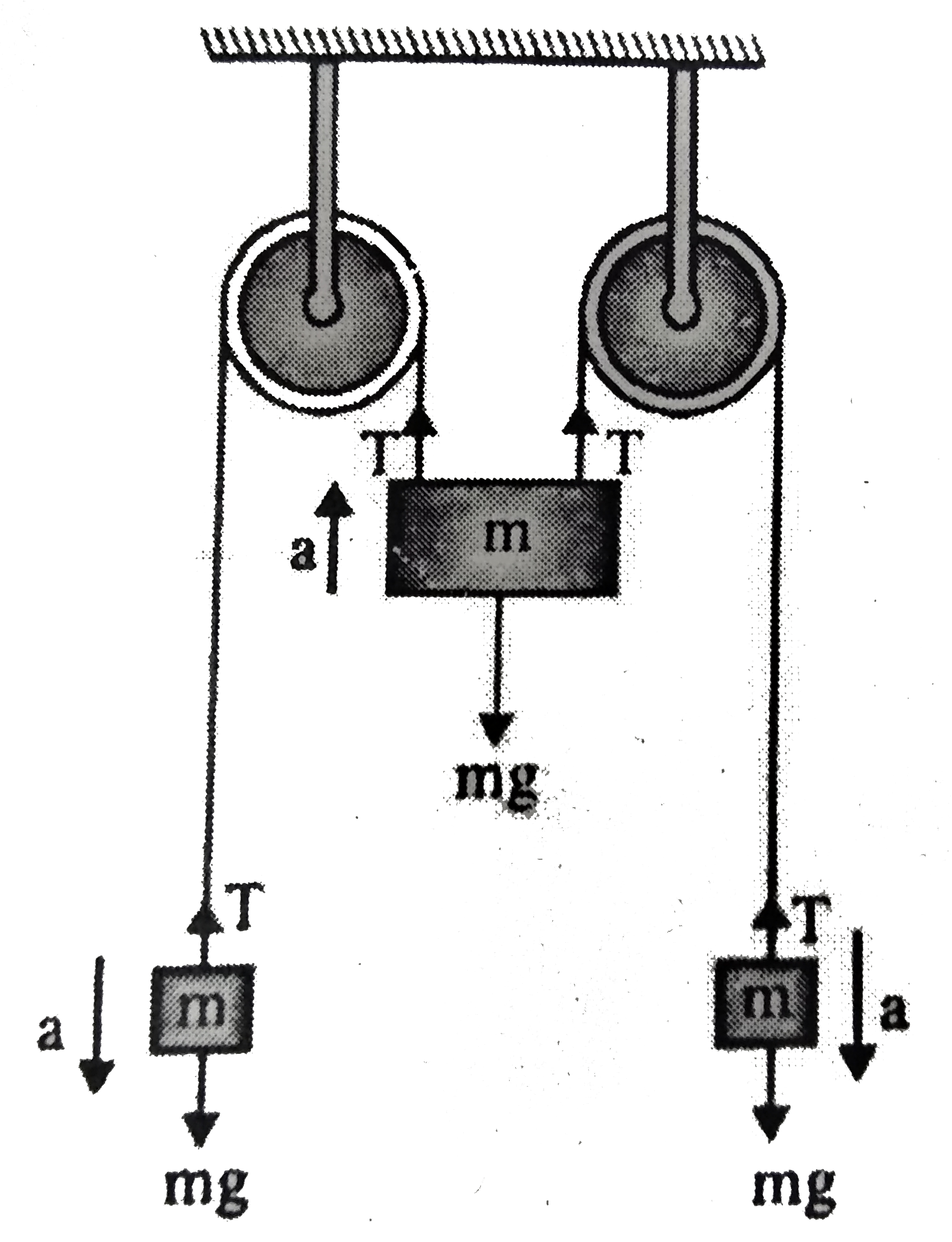
(a) What is acceleration of the masses?
(b) What is the tension in each string?
View SolutionFor the system shown in the figure, the pulleys are light and frictionless. The tension in the string will be (Assume all surfaces to be smooth)
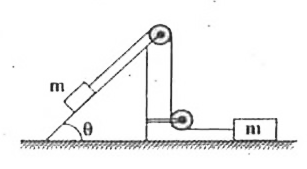
View Solution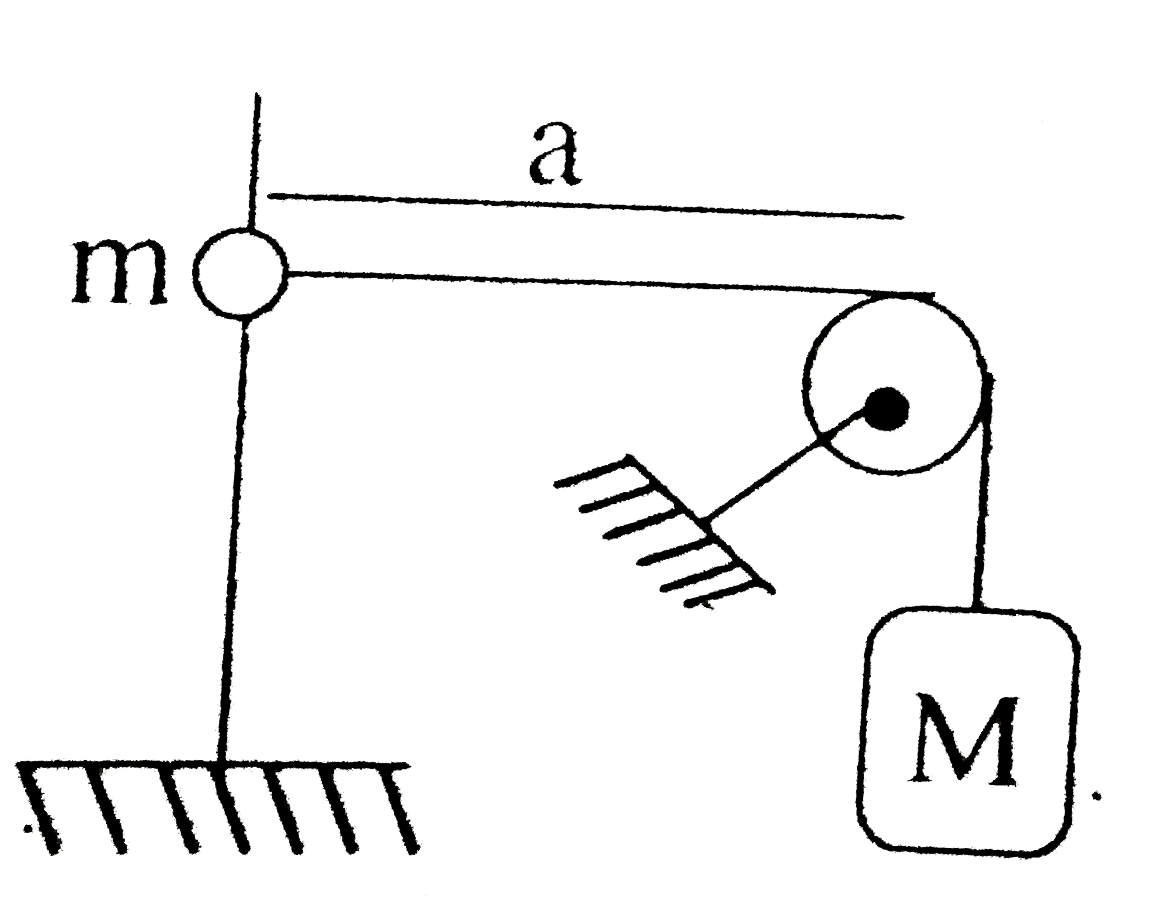
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string is
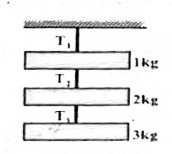
View SolutionDetermine the tensions T1 and T2 in the string as shown in figure.
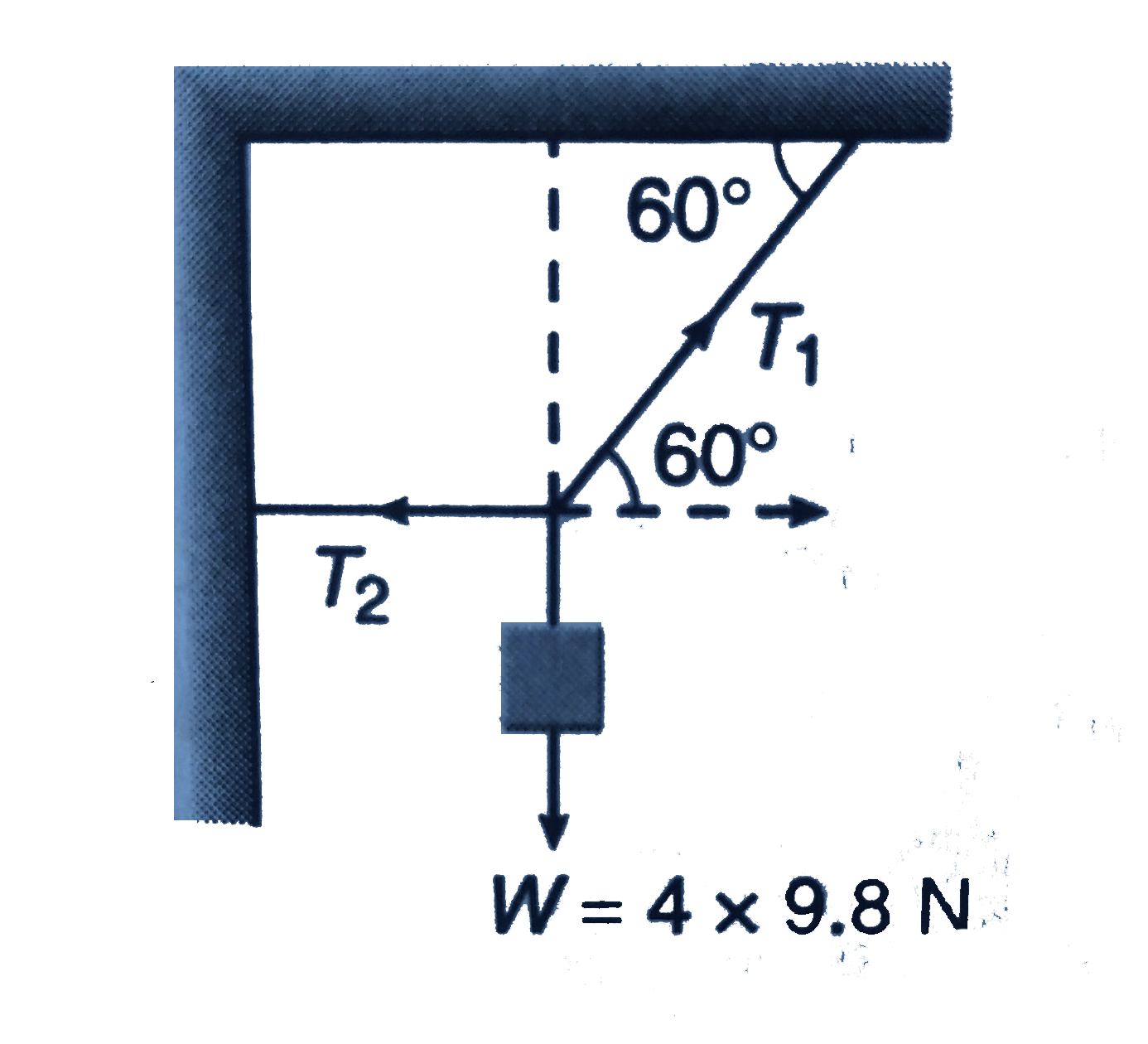
View Solution
