A non-uniform rod of mass m, length l and radius r is having its centre of mass at a distance l/4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is I. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

πρgl2r2I
πρgl2r24I
πρgl2r22I
3πρgl2r24I
The correct Answer is:B
Torque about CM
Fb14=ICMα or α1I(πr2)(1)(ρ)(g)14=πr212gρ4I 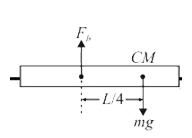
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -1
90 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A non-uniform cylinder of mass m, length l and radius r is having its centre of mass at a distance l.4 from the centre and lying on the axis of the cylinder. The cylinder is kept in a liquid of uniform density ρ. The moment of inertia of the rod about the centre of mass is l. The angular acceleration of point A relative to point B just after the rod is released from the position as shown in the figure is

View SolutionA non uniform cylinder of mass m, length l and radius r having its C.O.M at a distance l4 from centre and lying on axis of cylinder . The cylinder is kept in a liquid of unifrom density ρ. The moment of inertia of the rod about C.O.M is I. The angular acceleration of point A relative to point B just after the rod is released from position shown in figure is .

View SolutionA thin wire of length L and uniform linear mass density ρ is bent into a circular loop with centre at O as shown. The moment of inertia of the loop about the axis XX' is
View Solution
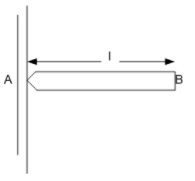
Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionA uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionA uniform rod AB of length l and mass m is free to rotate about an Axis passing through A and perpendicular to length of the rod. The rod is released from rest as shown in figure. Given that the moment of inertia of the rod about A is ml23 The initial angular acceleration of the rod will be
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionA thin uniform rod of mass M and length L. Find the radius of gyration for rotation about an axis passing through a point at a distance ofL4 from centre and perpendicular to rod.
View SolutionThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View Solution
