A sphere of radius R and made of material of relative density has a concentric cavity of radius r. It just floats when placed in a tank full of water. The value of the ratio will be
(a)
(b)
(c)
(d)
The correct Answer is:C
To solve the problem, we need to apply the principle of flotation, which states that a floating body displaces its own weight of fluid. Let's break down the solution step by step.
1. Understanding the Problem:
- We have a sphere of radius R made of a material with relative density σ.
- There is a concentric cavity of radius r within the sphere.
- The sphere is floating in water, meaning the weight of the sphere equals the weight of the water displaced.
2. Weight of the Sphere:
- The volume of the sphere can be calculated as:
Vsphere=43πR3
- The volume of the cavity is:
Vcavity=43πr3
- Therefore, the effective volume of the sphere (considering the cavity) is:
Veffective=Vsphere−Vcavity=43π(R3−r3)
3. Weight of the Sphere:
- The weight of the sphere can be expressed as:
Wsphere=Veffective⋅density of sphere⋅g=43π(R3−r3)⋅(σ⋅ρwater)⋅g
- Here, ρwater is the density of water.
4. Weight of the Displaced Water:
- The weight of the water displaced by the sphere is equal to the volume of water displaced times the density of water:
Wdisplaced=Vdisplaced⋅ρwater⋅g=43πR3⋅ρwater⋅g
5. Setting the Weights Equal:
- According to the principle of flotation:
Wsphere=Wdisplaced
- Thus, we have:
43π(R3−r3)⋅(σ⋅ρwater)⋅g=43πR3⋅ρwater⋅g
6. Canceling Common Terms:
- Cancel out the common terms 43πg and ρwater:
(R3−r3)⋅σ=R3
7. Rearranging the Equation:
- Rearranging gives:
R3−r3=R3σ
- This simplifies to:
R3(1−1σ)=r3
8. Finding the Ratio:
- Taking the cube root on both sides:
r=R(1−1σ)1/3
- Thus, the ratio Rr can be expressed as:
Rr=RR(1−1σ)1/3=1(1−1σ)1/3
9. Final Expression:
- Therefore, the final expression for the ratio Rr is:
Rr=(σσ−1)1/3
Conclusion:
The value of the ratio Rr is (σσ−1)1/3.
- We have a sphere of radius R made of a material with relative density σ.
- There is a concentric cavity of radius r within the sphere.
- The sphere is floating in water, meaning the weight of the sphere equals the weight of the water displaced.
- The volume of the sphere can be calculated as:
Vsphere=43πR3
- The volume of the cavity is:
Vcavity=43πr3
- Therefore, the effective volume of the sphere (considering the cavity) is:
Veffective=Vsphere−Vcavity=43π(R3−r3)
- The weight of the sphere can be expressed as:
Wsphere=Veffective⋅density of sphere⋅g=43π(R3−r3)⋅(σ⋅ρwater)⋅g
- Here, ρwater is the density of water.
- The weight of the water displaced by the sphere is equal to the volume of water displaced times the density of water:
Wdisplaced=Vdisplaced⋅ρwater⋅g=43πR3⋅ρwater⋅g
- According to the principle of flotation:
Wsphere=Wdisplaced
- Thus, we have:
43π(R3−r3)⋅(σ⋅ρwater)⋅g=43πR3⋅ρwater⋅g
- Cancel out the common terms 43πg and ρwater:
(R3−r3)⋅σ=R3
- Rearranging gives:
R3−r3=R3σ
- This simplifies to:
R3(1−1σ)=r3
- Taking the cube root on both sides:
r=R(1−1σ)1/3
- Thus, the ratio Rr can be expressed as:
Rr=RR(1−1σ)1/3=1(1−1σ)1/3
- Therefore, the final expression for the ratio Rr is:
Rr=(σσ−1)1/3
The value of the ratio Rr is (σσ−1)1/3.
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL -2
Explore 50 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL-0 ( Short Answer Type - II )
Explore 15 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions
A sphere of solid material of specific gravity 8 has a concentric spherical cavity and just sinks in water. The ratio of radius of cavity to that of outer radius of the sphere must be
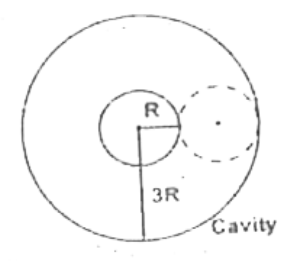
View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density σc/m3. It has a spherical cavity of radius R as shown in the figure. The electric field at the centre of the cavity is
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?
View SolutionA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.
Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?

View SolutionA conducting sphere of radius r has a charge . Then .
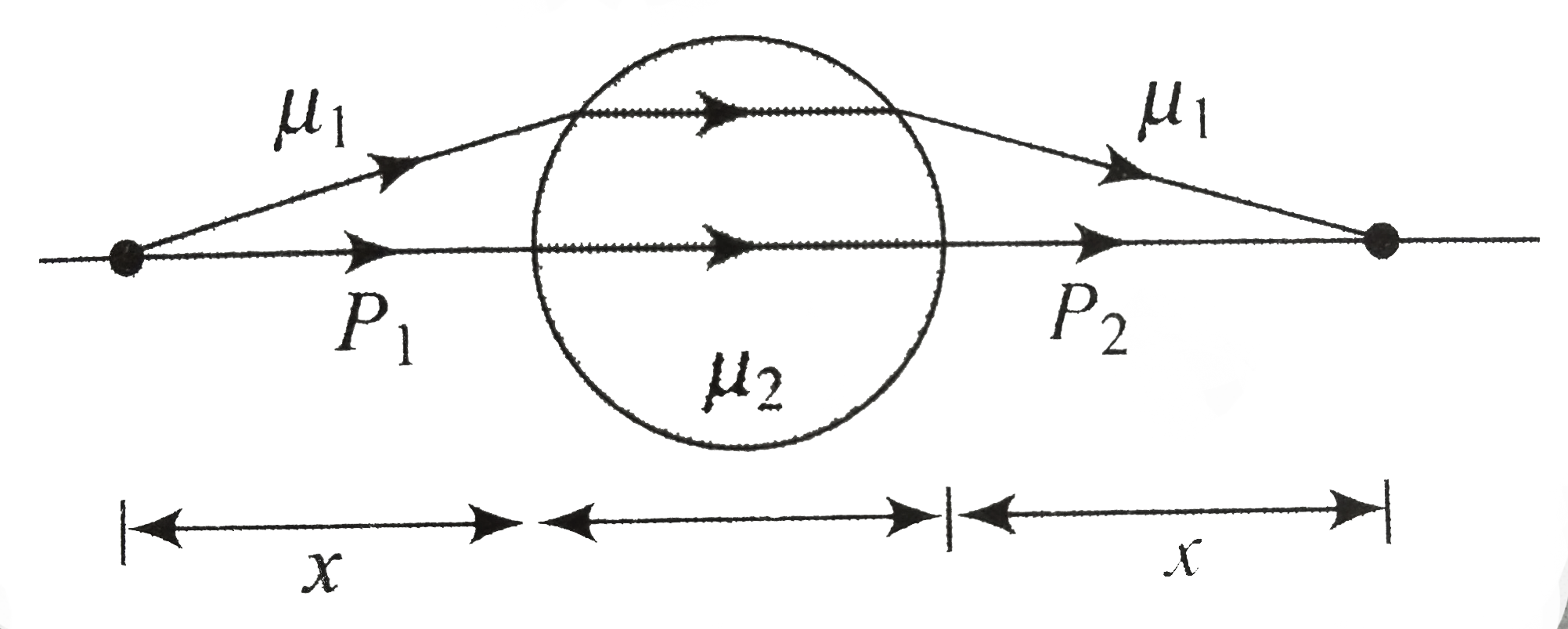
View SolutionA sphere of radius R made of material of refractive index μ2 is placed in a medium of refractive index μ1. Where would an object be placed so that a real image is formed at equidistant fromk the sphere? ltbgt
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)
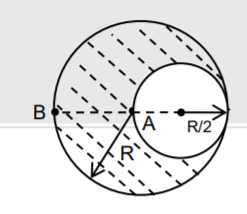
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?

View Solution
