A conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :
(a)zero
(b)kq1r−kq1R1
(c)kq1r−kq1R1+Kq1R2
(d)None of these
The correct Answer is:C
To find the electric potential at the center of the cavity of a conducting sphere with a point charge placed inside it, we can follow these steps:
1. Understanding the Setup:
- We have a conducting sphere of radius R2 with a spherical cavity of radius R1 that is non-concentric.
- A point charge q1 is placed at a distance r from the center of the cavity.
2. Applying Gauss's Law:
- Since the sphere is conducting, the electric field inside the conductor itself is zero.
- The charge q1 will induce a charge of −q1 on the inner surface of the cavity.
- Consequently, a charge of +q1 will appear on the outer surface of the conducting sphere.
3. Electric Potential Calculation:
- The electric potential V at a point due to a point charge is given by the formula:
V=kqr
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
4. Potential at the Center of the Cavity:
- The total electric potential at the center of the cavity O can be calculated as the sum of the potentials due to:
- The point charge q1
- The induced charge on the inner surface of the cavity −q1
- The charge on the outer surface of the conductor +q1
5. Calculating Each Contribution:
- The potential due to the point charge q1 at the center of the cavity:
Vq1=kq1d1
where d1 is the distance from q1 to the center of the cavity.
- The potential due to the induced charge −q1 on the inner surface:
V−q1=−kq1R1
- The potential due to the outer surface charge +q1:
V+q1=kq1R2
6. Total Electric Potential:
- The total electric potential at the center of the cavity is:
Vtotal=Vq1+V−q1+V+q1
- Substituting the contributions:
Vtotal=kq1d1−kq1R1+kq1R2
7. Final Expression:
- Thus, the electric potential at the center of the cavity is:
V=kq1(1d1−1R1+1R2)
Conclusion:
The electric potential at the center of the cavity is given by the expression derived above.
- We have a conducting sphere of radius R2 with a spherical cavity of radius R1 that is non-concentric.
- A point charge q1 is placed at a distance r from the center of the cavity.
- Since the sphere is conducting, the electric field inside the conductor itself is zero.
- The charge q1 will induce a charge of −q1 on the inner surface of the cavity.
- Consequently, a charge of +q1 will appear on the outer surface of the conducting sphere.
- The electric potential V at a point due to a point charge is given by the formula:
V=kqr
where k is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where the potential is being calculated.
- The total electric potential at the center of the cavity O can be calculated as the sum of the potentials due to:
- The point charge q1
- The induced charge on the inner surface of the cavity −q1
- The charge on the outer surface of the conductor +q1
- The potential due to the point charge q1 at the center of the cavity:
Vq1=kq1d1
where d1 is the distance from q1 to the center of the cavity.
- The potential due to the induced charge −q1 on the inner surface:
V−q1=−kq1R1
- The potential due to the outer surface charge +q1:
V+q1=kq1R2
- The total electric potential at the center of the cavity is:
Vtotal=Vq1+V−q1+V+q1
- Substituting the contributions:
Vtotal=kq1d1−kq1R1+kq1R2
- Thus, the electric potential at the center of the cavity is:
V=kq1(1d1−1R1+1R2)
The electric potential at the center of the cavity is given by the expression derived above.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
A conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R.The distance r<R.The electric potential at the centre of the shell will be

View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
View SolutionA sphare of mass M and radiusR2 has a concentric cavity of radius R1 as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0≤r≤∞) .
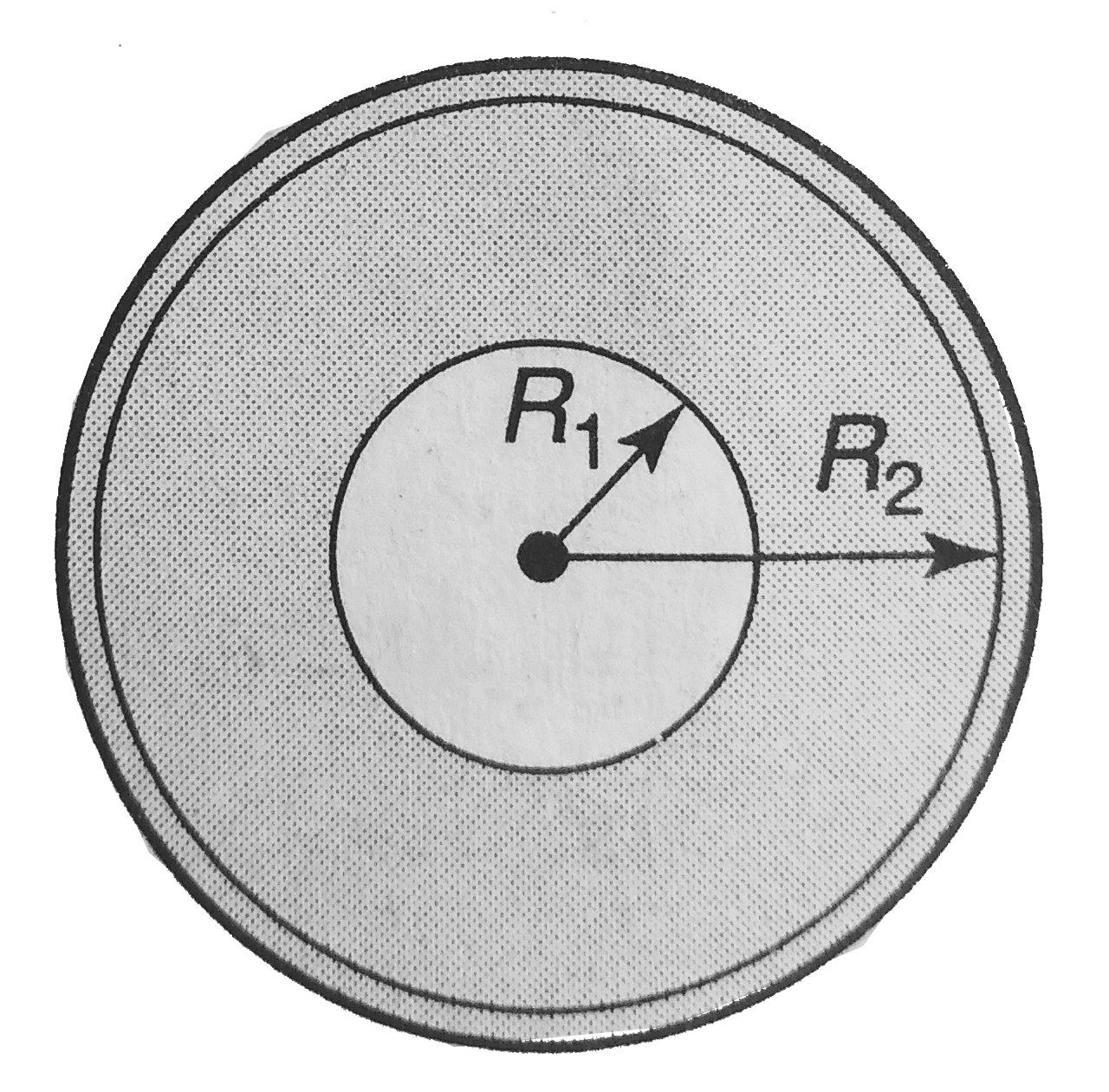
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

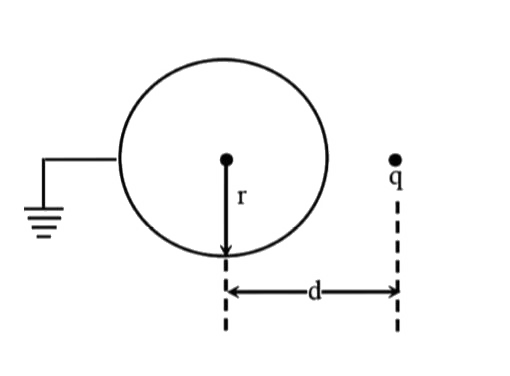
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA conducting sphere of radius b has a spherical cavity with its centre displaced by 'a' from centre of sphere O1. A point charged q is placed at the centre of cavity O2. Q charge is given to conducting sphere and charge q0 is placed at P, a distance c from centre O1. Further O1,O2 and P are collinear

View Solution
