A conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
If q1 is shifted to the centre of the cavity, then: (choose the correct alternative)
electric field in the region outside sphere may change
electric potential in the region outside sphere may change
electrostatic energy stored in the system may change
electric potential of sphere may change
The correct Answer is:C
To solve the problem step by step, we need to analyze the situation of a conducting sphere with a spherical cavity and a point charge placed within that cavity. The charge is then shifted to the center of the cavity. Let's break down the solution:
Step 1: Understand the System
We have a conducting sphere of radius R2 with a spherical cavity of radius R1 that is non-concentric with the sphere. A point charge q1 is initially placed at a distance r from the center of the cavity.
Hint: Visualize the arrangement of the conducting sphere and the cavity to understand how the charge affects the electric field and potential.
Step 2: Initial Conditions
When the charge q1 is placed at a distance r from the center of the cavity, it induces a charge on the inner surface of the cavity. The conducting material will redistribute its free charges to maintain electrostatic equilibrium.
Hint: Remember that the electric field inside a conductor in electrostatic equilibrium is zero, and the induced charge on the cavity surface will depend on the position of q1.
Step 3: Shift the Charge to the Center
Now, we shift the charge q1 to the center of the cavity. This change will affect the distribution of the induced charge on the inner surface of the cavity.
Hint: Consider how the symmetry of the charge distribution changes when q1 is moved to the center.
Step 4: Analyze the Electric Field Outside the Sphere
According to Gauss's law, the electric field outside the conducting sphere depends only on the total charge enclosed within the Gaussian surface. Since the total charge on the conducting sphere remains constant, the electric field outside the sphere does not change when q1 is moved.
Hint: Use Gauss's law to conclude that the electric field outside the conducting sphere remains unchanged.
Step 5: Analyze the Electric Potential Outside the Sphere
Since the electric field outside the sphere does not change, the electric potential outside the sphere also remains constant.
Hint: Recall that electric potential is related to electric field through the relationship E=−dVdr.
Step 6: Electrostatic Energy in the System
The electrostatic energy stored in the system is related to the configuration of the charges. When q1 is moved to the center, the potential energy associated with the charge configuration may change due to the change in the potential at the location of the charge.
Hint: Consider how the potential energy depends on the position of the charge within the cavity.
Step 7: Electric Potential of the Sphere
The conducting sphere maintains an equipotential surface. The potential of the sphere does not change because the charge distribution on the surface remains uniform regardless of the position of q1.
Hint: Remember that the potential on the surface of a conductor in electrostatic equilibrium is constant.
Conclusion
Based on the analysis:
- The electric field outside the sphere does not change.
- The electric potential outside the sphere does not change.
- The electrostatic energy in the system may change when q1 is moved to the center.
- The electric potential of the sphere remains constant.
Thus, the correct alternative is that the electrostatic energy stored in the system may change.
Final Answer
The correct alternative is: Electrostatic energy stored in the system may change.
We have a conducting sphere of radius R2 with a spherical cavity of radius R1 that is non-concentric with the sphere. A point charge q1 is initially placed at a distance r from the center of the cavity.
When the charge q1 is placed at a distance r from the center of the cavity, it induces a charge on the inner surface of the cavity. The conducting material will redistribute its free charges to maintain electrostatic equilibrium.
Now, we shift the charge q1 to the center of the cavity. This change will affect the distribution of the induced charge on the inner surface of the cavity.
According to Gauss's law, the electric field outside the conducting sphere depends only on the total charge enclosed within the Gaussian surface. Since the total charge on the conducting sphere remains constant, the electric field outside the sphere does not change when q1 is moved.
Since the electric field outside the sphere does not change, the electric potential outside the sphere also remains constant.
The electrostatic energy stored in the system is related to the configuration of the charges. When q1 is moved to the center, the potential energy associated with the charge configuration may change due to the change in the potential at the location of the charge.
The conducting sphere maintains an equipotential surface. The potential of the sphere does not change because the charge distribution on the surface remains uniform regardless of the position of q1.
Based on the analysis:
- The electric field outside the sphere does not change.
- The electric potential outside the sphere does not change.
- The electrostatic energy in the system may change when q1 is moved to the center.
- The electric potential of the sphere remains constant.
The correct alternative is: Electrostatic energy stored in the system may change.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 1
105 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Video
Similar Questions
A conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :
View SolutionA sphare of mass M and radiusR2 has a concentric cavity of radius R1 as shown in figure The force F exerted by the sphere on a particle of mass m located at a distance r from the centre of sphere veries as (0≤r≤∞) .
View SolutionA point charge q , is placed at a distance r from the centre of an aluminium sphere, of radius R (r>R) . Selectr the correct alternatives.
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA conducting sphere of radius b has a spherical cavity with its centre displaced by 'a' from centre of sphere O1. A point charged q is placed at the centre of cavity O2. Q charge is given to conducting sphere and charge q0 is placed at P, a distance c from centre O1. Further O1,O2 and P are collinear

View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
View SolutionA solid metal sphere of radius R has a charg +2Q. A hollow spherical shell of radius 3R placed concentric with the frist sphere has net charge -Q.
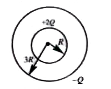
What would be the final distribution of charges if the sphres are joined by a conducting wire
View Solution
