A square gate of size 1m×1m is hinged at its mid point. A fluid of density ρ fill the space to the left of the gate. The force F required to hold the gate stationary is

ρg3
ρg2
ρg6
ρg8
The correct Answer is:C
Force on elemental strip at depth x due to water
dF=ρgx×1dx,(τCM=F×12+∫dτw
τCM=F×12+∫10ρgxdx(12−x),τCM=0, Hence F=(ρg6)
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -2
50 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )
15 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A light semi cylindrical gate of radius R is pivoted aat its mid point O, of radius R as shown in the figure holding liquid of density ρ. The force F required to prevent the rotation of the gate is equal to

View SolutionThe rectangualr wire- frame, shown in has a width d, mass m, resistance R and a large length. A uniform magnetic field B exists to the left of the frame. A constant force F starts pushing the frame into the magnetic field at t =0. (a) Find the acceleration of the frame when its speed has increased to v. (b) Show that after some time the frame will move with a constant velocity till the whole frame enters into the magnetic field. find this velocity v0. (c) show that the velocity at tiem t is given by v=v0(1−e−Ftmv0.
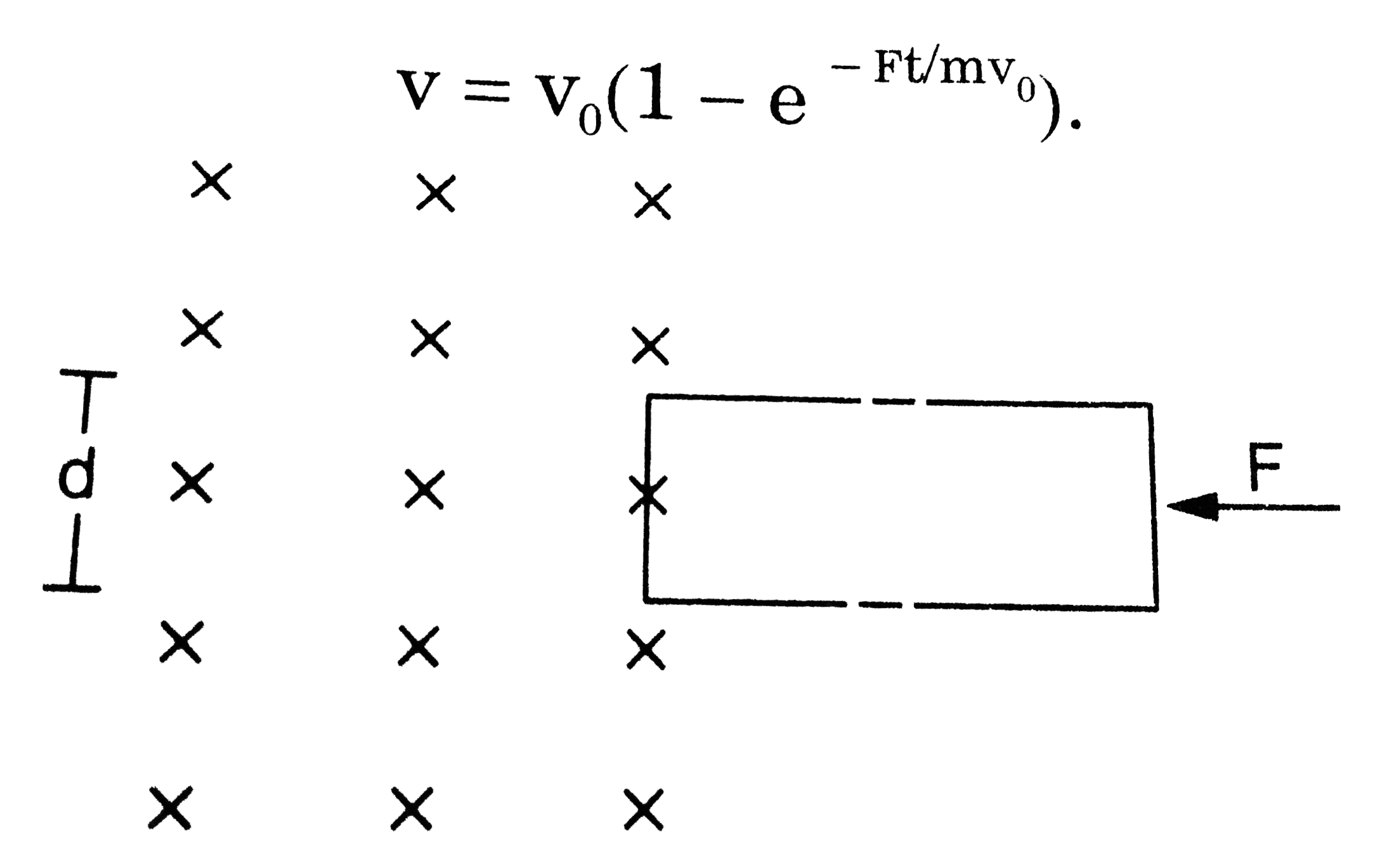
View Solution
Knowledge Check
A tank with a square base of area 2m2 is divided into two compartments by a vertical partition in the middle. There is a small hinged door of face area 20cm2 at the bottom of the partition. Water is filled in one compartment and an acid of relative density 1.5 in the other, both to a height of 4m. The force necessary to keep the door closed is (Takeg=10ms−2)
A10NB20 NC40 ND80 N
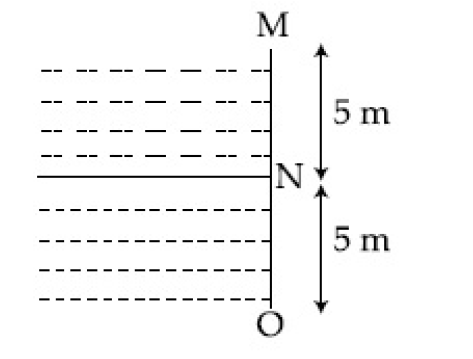 Two liquids of densities ρ1 and ρ2(ρ2=2ρ1) are filled up behind a square wall of side 10 m as shown in the figure. Each liquids has a height of 5m. The ratio of the forces due to these liqyuids exeted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing):
Two liquids of densities ρ1 and ρ2(ρ2=2ρ1) are filled up behind a square wall of side 10 m as shown in the figure. Each liquids has a height of 5m. The ratio of the forces due to these liqyuids exeted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing):
View SolutionTwo liquids of densities ρ1 and ρ2(ρ2=3ρ1) are filled up behind a square wall of side 6 m as shown in figure. Each liquid has a height of 3 m. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)2
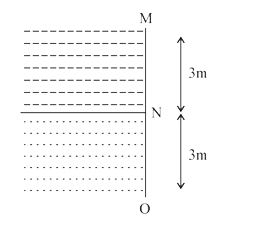
View SolutionTwo liquids of densities ρ1 and ρ2(ρ2=3ρ1) are filled up behind a square wall of side 6 m as shown in figure. Each liquid has a height of 3 m. The ratio of the forces due to these liquids exerted on upper part MN to that at the lower part NO is (Assume that the liquids are not mixing)2

View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionDuring a heavy rain hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10m×10m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900kgm3
View SolutionDuring a heavy rain hailstones of average size 1.0 cm in diameter fall with an average speed of 20 m/s. Suppose 2000 hailstones strike every square meter of a 10m×10m roof perpendicularly in one second and assume that the hailstones do not rebound. Calculate the average force exerted by the falling hailstones on the roof. Density of a hailstone is 900kgm3
View SolutionSelvis house has an overhead tank in the shape of a cylinder. This is filled by pumping water from a sump (an underground tank) which is in the shape of a cuboid. The sump has dimensions 1.57m×1.44m×95cm. The overhead tank has its radius of 60cm and its height is 95cm. Find the height of the water, left in the sump after the overhead tank has been completely filled with water from a sump which had been full. Compare the capacity of the tank with that of the sump (Use π=22/7)
View Solution
