A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
(a)8 cm
(b)2 cm
(c)40 cm
(d)4 cm
The correct Answer is:A
To solve the problem, we need to determine the difference in height of the liquid at the center of the cylindrical vessel and at its sides when the vessel is rotated. Here are the steps to arrive at the solution:
Step 1: Identify the given values
- Radius of the vessel, r=5cm=0.05m
- Speed of rotation, f=4rev/s
Step 2: Convert the speed of rotation to angular velocity
Angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the given value:
ω=2π×4=8πrad/s
Step 3: Apply Bernoulli's equation
We apply Bernoulli's equation between the center of the vessel and the side of the vessel. The pressure difference can be expressed as:
P1−P2=12ρv2
Where P1 is the pressure at the center, P2 is the pressure at the side, ρ is the density of the liquid, and v is the linear velocity at the side of the vessel.
Step 4: Calculate the linear velocity at the side
The linear velocity v at the side of the vessel is given by:
v=rω
Substituting the values:
v=0.05×8π=0.4πm/s
Step 5: Substitute into Bernoulli's equation
The pressure difference can now be expressed as:
P1−P2=12ρ(0.4π)2
Step 6: Relate pressure difference to height difference
The pressure difference can also be expressed in terms of height difference h:
P1−P2=ρgh
Equating the two expressions for pressure difference:
ρgh=12ρ(0.4π)2
The density ρ cancels out:
gh=12(0.4π)2
Step 7: Solve for height difference h
Rearranging gives:
h=(0.4π)22g
Substituting g≈10m/s2:
h=(0.4π)220
Step 8: Calculate the value of h
Calculating (0.4π)2:
(0.4π)2=0.16π2
Thus,
h=0.16π220=0.008π2m
Calculating π2≈9.87:
h≈0.008×9.87≈0.079m≈8cm
Final Answer
The difference in height of the liquid at the center of the vessel and its sides is approximately 8 cm.
---
- Radius of the vessel, r=5cm=0.05m
- Speed of rotation, f=4rev/s
Angular velocity ω in radians per second can be calculated using the formula:
ω=2πf
Substituting the given value:
ω=2π×4=8πrad/s
We apply Bernoulli's equation between the center of the vessel and the side of the vessel. The pressure difference can be expressed as:
P1−P2=12ρv2
Where P1 is the pressure at the center, P2 is the pressure at the side, ρ is the density of the liquid, and v is the linear velocity at the side of the vessel.
The linear velocity v at the side of the vessel is given by:
v=rω
Substituting the values:
v=0.05×8π=0.4πm/s
The pressure difference can now be expressed as:
P1−P2=12ρ(0.4π)2
The pressure difference can also be expressed in terms of height difference h:
P1−P2=ρgh
Equating the two expressions for pressure difference:
ρgh=12ρ(0.4π)2
The density ρ cancels out:
gh=12(0.4π)2
Rearranging gives:
h=(0.4π)22g
Substituting g≈10m/s2:
h=(0.4π)220
Calculating (0.4π)2:
(0.4π)2=0.16π2
Thus,
h=0.16π220=0.008π2m
Calculating π2≈9.87:
h≈0.008×9.87≈0.079m≈8cm
The difference in height of the liquid at the center of the vessel and its sides is approximately 8 cm.
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL -2
Explore 50 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:LEVEL-0 ( Short Answer Type - II )
Explore 15 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
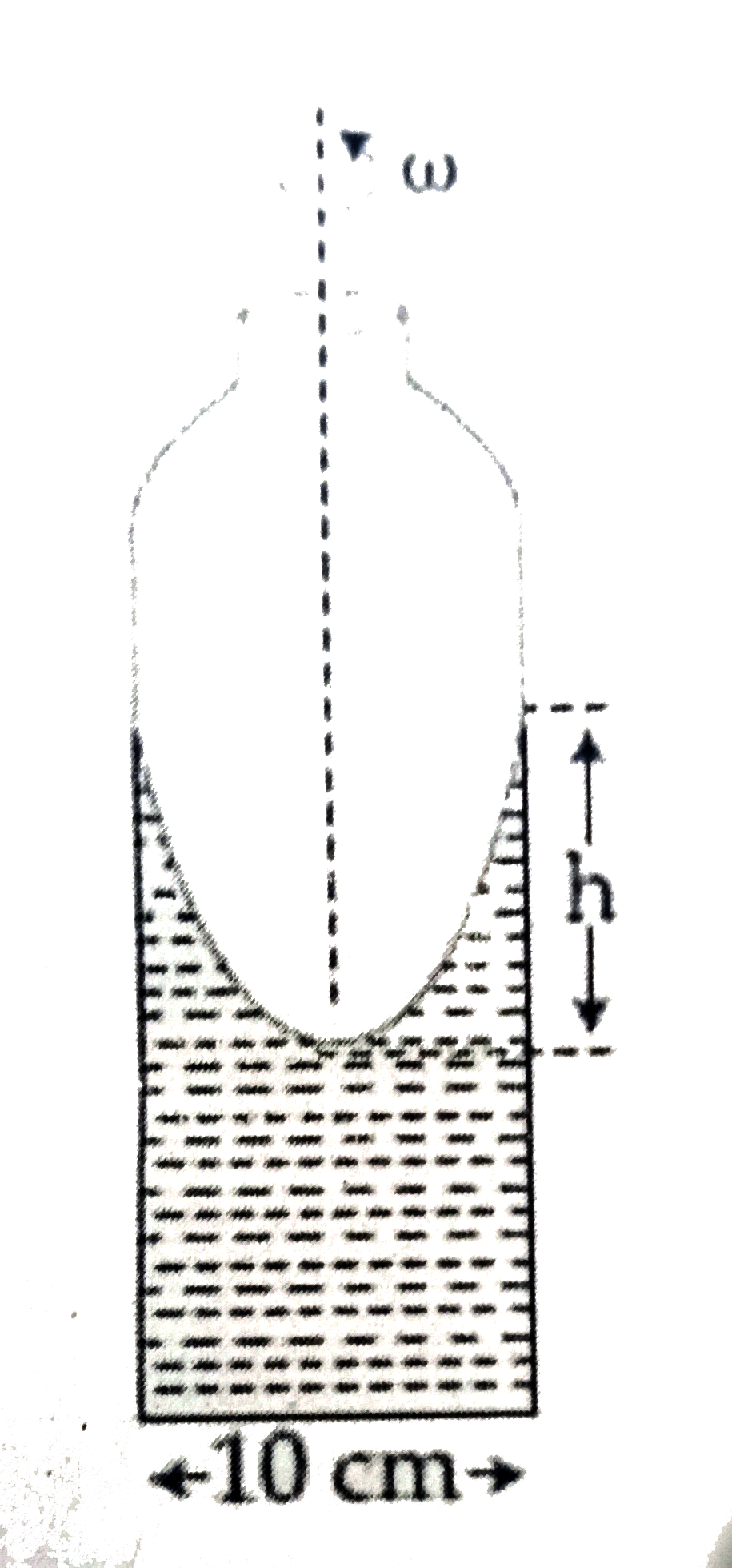
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000 cm2
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000cm2.
View SolutionA cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of Rs. 3.50 per 1000cm2.
View SolutionA fluid having a thermal coefficient of volume expansion γ is filled in a cylindrical vessel up to a height h0. The coefficient of linear thermal expansion of the material of the vessel is α . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by Δθ.
View Solution