A cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity then what is the difference of the heights of liquid at centre of vessel and edge?
To solve the problem, we need to find the difference in height of the liquid at the center of a rotating cylindrical vessel and at its edge. Let's go through the solution step by step.
1. Understand the Setup:
- We have a cylindrical vessel of radius r filled with liquid.
- The vessel is rotating about a vertical axis with angular velocity ω.
- We need to find the difference in height of the liquid at the center (point A) and at the edge (point B) of the vessel.
2. Identify Points:
- Let hA be the height of the liquid at the center (point A).
- Let hB be the height of the liquid at the edge (point B).
- We need to find the difference hB−hA.
3. Apply Bernoulli's Theorem:
- According to Bernoulli's theorem, the total mechanical energy along a streamline is constant. The equation is given by:
P+12ρv2+ρgh=constant
- We will apply this theorem at points A and B.
4. Set Up the Bernoulli Equation:
- For point A (center):
PA+0+ρghA=constant
- For point B (edge):
PB+12ρv2B+ρghB=constant
- Here, vA=0 (since the center does not have any tangential velocity) and vB=rω (the tangential velocity at the edge).
5. Express Pressures:
- Let PA=P0 (atmospheric pressure) and PB=P0+ρghB.
- Substitute these into the Bernoulli equations:
P0+ρghA=P0+12ρ(rω)2+ρghB
6. Simplify the Equation:
- Cancel P0 from both sides:
ρghA=12ρ(rω)2+ρghB
- Rearranging gives:
ρghA−ρghB=12ρ(rω)2
7. Factor Out Common Terms:
- Dividing through by ρ:
g(hA−hB)=12(r2ω2)
- Thus, we have:
hB−hA=r2ω22g
8. Final Result:
- The difference in height of the liquid at the edge and the center of the vessel is:
hB−hA=r2ω22g
- We have a cylindrical vessel of radius r filled with liquid.
- The vessel is rotating about a vertical axis with angular velocity ω.
- We need to find the difference in height of the liquid at the center (point A) and at the edge (point B) of the vessel.
- Let hA be the height of the liquid at the center (point A).
- Let hB be the height of the liquid at the edge (point B).
- We need to find the difference hB−hA.
- According to Bernoulli's theorem, the total mechanical energy along a streamline is constant. The equation is given by:
P+12ρv2+ρgh=constant
- We will apply this theorem at points A and B.
- For point A (center):
PA+0+ρghA=constant
- For point B (edge):
PB+12ρv2B+ρghB=constant
- Here, vA=0 (since the center does not have any tangential velocity) and vB=rω (the tangential velocity at the edge).
- Let PA=P0 (atmospheric pressure) and PB=P0+ρghB.
- Substitute these into the Bernoulli equations:
P0+ρghA=P0+12ρ(rω)2+ρghB
- Cancel P0 from both sides:
ρghA=12ρ(rω)2+ρghB
- Rearranging gives:
ρghA−ρghB=12ρ(rω)2
- Dividing through by ρ:
g(hA−hB)=12(r2ω2)
- Thus, we have:
hB−hA=r2ω22g
- The difference in height of the liquid at the edge and the center of the vessel is:
hB−hA=r2ω22g
Similar Questions
A cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View SolutionA rod is rotating with angular velocity ω about axis AB. Find cosθ.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA horizontal disc is rotating about a vertical axis passing through its centre. If an insect moves from centre to rim then the angular momentum of the system
View SolutionA ring of mass m and radius r rotates about an axis passing through its centre and perpendicular to its plane with angular velocity ω. Its kinetic energy is
View SolutionIf the rod were translating as well as rotating, what will be its emf? Assume that the centre of mass has a velocity v and the rod is rotating with an angular velocity ω atout its centre of mass.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
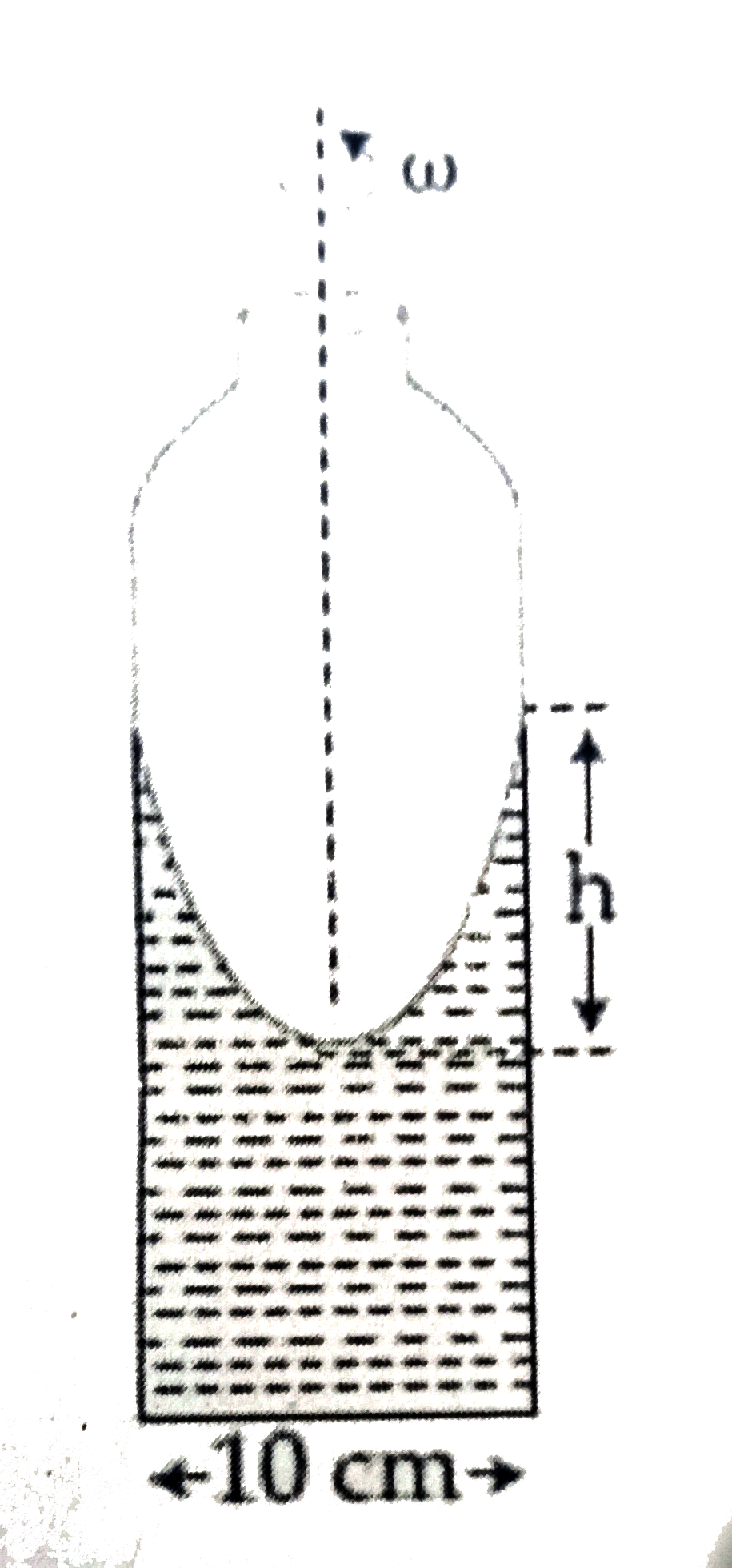
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
View SolutionA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
View Solution
