A liquid is kept in a cylindrical vessel which is being rotated about a vertical axis through the centre of the circular base. If the radius of the vessel is r and angular velocity of rotation is ω, then the difference in the heights of the liquid at the centre of the vessel and the edge is.
rω2g
r2ω22g
√2grω
ω22gr2
The correct Answer is:B
PA+12ρv2A+ρghA=PB+12ρv2B+ρghB
hA=hB
PA−PB=12ρ(v2B−v2A)
vA=0,vB=rω,PA−PB=ρgh
ρgh=12ρr2ω2
h=r2ω22g.
 .
.
Topper's Solved these Questions
Similar Questions
The product of the numbers 5623 and 6 in the scale of eight is
View SolutionA cylinder vessel of radius 10 cm containing a liquid is rotating about a vertical axis through the centre of circular base. The vessel is rotating with angular frequency 10 rad/s. Find the difference of the heights of liquid at centre of vessel and edge.
View Solution
Knowledge Check
A cylindrical vessel of radius r containing a liqiud is rotating about a vertical axis through the centre of circular base, If the vessel is rotating with angular velocity ω then what is the difference of the heights of liquid at centre of vessel and edge?
Arω2gBr2ω22gC√2grωDω22gr2A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the side. If the radius of the vessel is 5cm and the speed of rotation is 4rev/s, then the difference in the height of the liquid at the centre of the vessel and its sides is
A8cmB2cmC40cmD4cmA liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides. If the radius of the vessel is r and the speed of revolution is n rotations/second, find the difference in height of the liquid at the centre of vessel and its sides.
Ah=2π2n2r2gBh=4π2n2r2gCh=π2r2n2gDh=π2r2n2g
A liquid is kept in a cylindrical vessel which is rotated along its axis. The liquid rises at the sides, if the radius of vessel is 0.05m and the speed of rotation is 2rev/s, find difference in the height of the liquid at the centre of the vessel and its sides.
View SolutionA cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure . The radius of vessel is 5 cm and the angular speed of rotation is ω rad s−1. The difference in the height , h ( in cm ) of liquid at the centre of vessel and at the side will be :
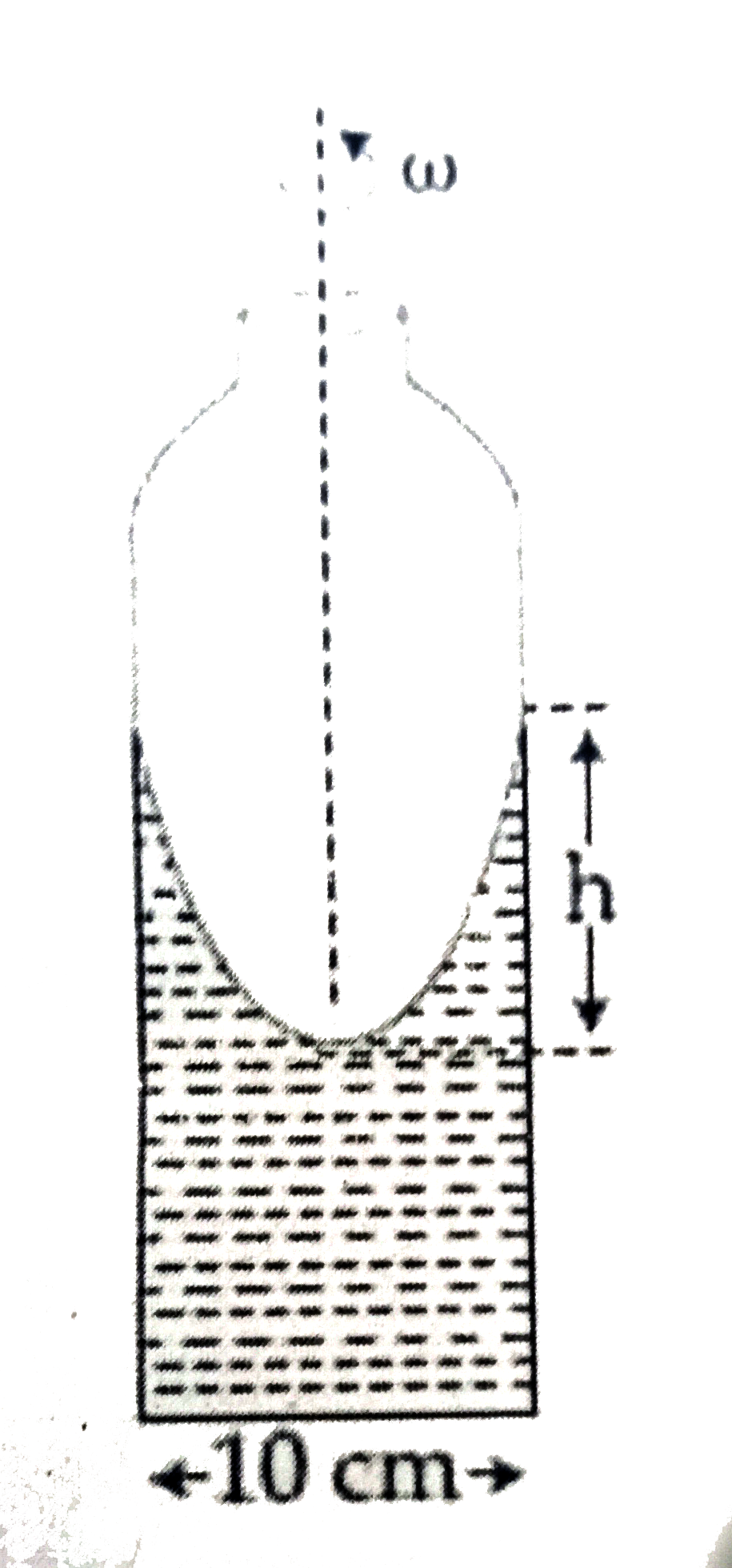
View SolutionA long cylindrical vessel is half filled with a liquid. When the vessel is rotated about its own vertical axis, the liquid rises up near the wall. If the radius of vessel is 5 cm and its rotational speed is 2 rotations per second, then the difference in the heights between the centre and the sides, in cm, will be:
View SolutionA liquid is kept in a cylindrical jar, which is rotated about the cylindrical axis. The liquid rises at its sides. The radius of the jar is r and speed of rotation is Ω the difference in height at the centre and the sides of the jar is
View SolutionA liquid kept in a cylindrical vessel of radius 0.3 m is rotated with a speed 2 r.p.s. The difference in the height of the liquid at the centre of the vessel and at it's sides it
View Solution

