A liquid of density ρ comes out with a velocity v from a horizontal tube of area of cross-section A. The reaction force exerted by the liquid on the tube is F. Choose the incorrect option.
F∝v
F∝v2
F∝A
F∝ρ
The correct Answer is:A
To solve the problem, we need to analyze the relationship between the reaction force F exerted by the liquid on the tube and the various parameters given: density ρ, velocity v, and cross-sectional area A.
1. Understanding the Flow of Liquid:
- The liquid is flowing out of a tube with a certain velocity v and has a density ρ. The area of cross-section of the tube is A.
2. Calculating Mass Flow Rate:
- The mass flow rate ˙m of the liquid can be calculated using the formula:
˙m=ρ⋅A⋅v
- Here, ˙m represents the mass of liquid flowing out per unit time.
3. Applying Newton's Second Law:
- According to Newton's second law, the force exerted by the liquid can be related to the change in momentum. The momentum per unit time (which is the force) is given by:
F=˙m⋅v=(ρ⋅A⋅v)⋅v=ρ⋅A⋅v2
4. Identifying Relationships:
- From the equation F=ρ⋅A⋅v2, we can derive the following relationships:
- F is proportional to v2: F∝v2
- F is proportional to A: F∝A
- F is proportional to ρ: F∝ρ
5. Choosing the Incorrect Option:
- The question asks to choose the incorrect option. The relationships derived indicate that:
- F is proportional to v2 (correct)
- F is proportional to A (correct)
- F is proportional to ρ (correct)
- Any statement suggesting F is proportional to v (not v2) would be incorrect.
Conclusion:
The incorrect option is the one that states F is proportional to v instead of v2.
- The liquid is flowing out of a tube with a certain velocity v and has a density ρ. The area of cross-section of the tube is A.
- The mass flow rate ˙m of the liquid can be calculated using the formula:
˙m=ρ⋅A⋅v
- Here, ˙m represents the mass of liquid flowing out per unit time.
- According to Newton's second law, the force exerted by the liquid can be related to the change in momentum. The momentum per unit time (which is the force) is given by:
F=˙m⋅v=(ρ⋅A⋅v)⋅v=ρ⋅A⋅v2
- From the equation F=ρ⋅A⋅v2, we can derive the following relationships:
- F is proportional to v2: F∝v2
- F is proportional to A: F∝A
- F is proportional to ρ: F∝ρ
- The question asks to choose the incorrect option. The relationships derived indicate that:
- F is proportional to v2 (correct)
- F is proportional to A (correct)
- F is proportional to ρ (correct)
- Any statement suggesting F is proportional to v (not v2) would be incorrect.
The incorrect option is the one that states F is proportional to v instead of v2.
Topper's Solved these Questions
Similar Questions
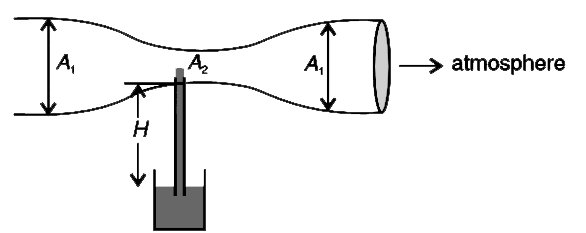
(i) Air (density=ρ) flows through a horizontal venturi tube that discharges to the atmosphere. The area of cross section of the tube is A1 and at the constriction it is A2. The constriction is connected to a water (density=ρ0) tank through a vertical pipe of lenght H. Find the volume flow rate (Q) of the air through tube that is needed to just draw the water into the tube.
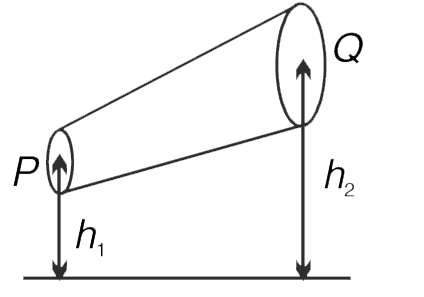
(ii) A non viscous liquid of constant density ρ flows in a stremline motion along a tube of variable cross section. The tube is kept inclined in the vertical plane as shown in the figure. The area of cross section of the tube at two points P and Q at heights of h1 and h2 are respectively A1 and A2. The velocity of the liquid at point P is v. Find the work done on a small volume ΔV of fluid by the neighbouring fluid as the small volume moves from P to Q.
View SolutionA liquid of density ρ flows along a horizontal pipe of uniform cross - section A with a velocity v through a right angled bend as shown in Fig. What force has to be exerted at the bend to hold the pipe in equilibrium ?
View Solution
Knowledge Check
The liquid inside the container has density ρ. Choose the correct option.
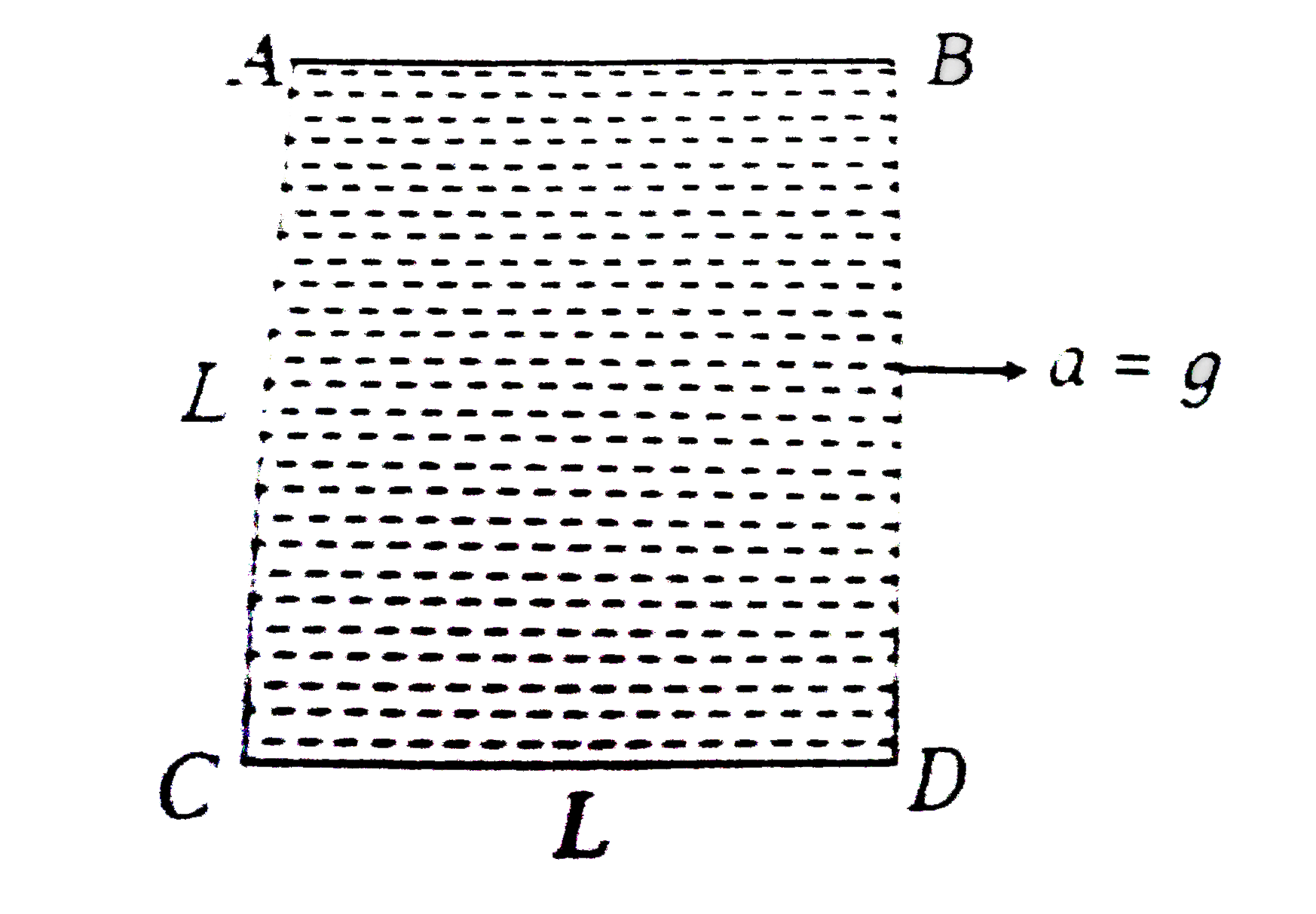 ApA−pC=2ρgLBpC−pB=√2ρgLCpC−pD=ρgLDpA−pD=0ρgL
ApA−pC=2ρgLBpC−pB=√2ρgLCpC−pD=ρgLDpA−pD=0ρgLAn ideal liquid of density ρ is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.
 A98ρAv2B54ρAv2C32ρAv2DρAv2
A98ρAv2B54ρAv2C32ρAv2DρAv2Two liquid columns of same height 5m and densities ρ and 2ρ are filled in a container of uniform cross sectional area. Then ratio of force exerted by the liquid on upper half of the wall to lower half of the wall is.
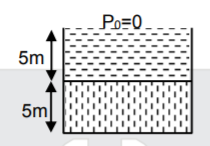 A14B12C13D23
A14B12C13D23
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
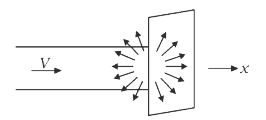
View Solution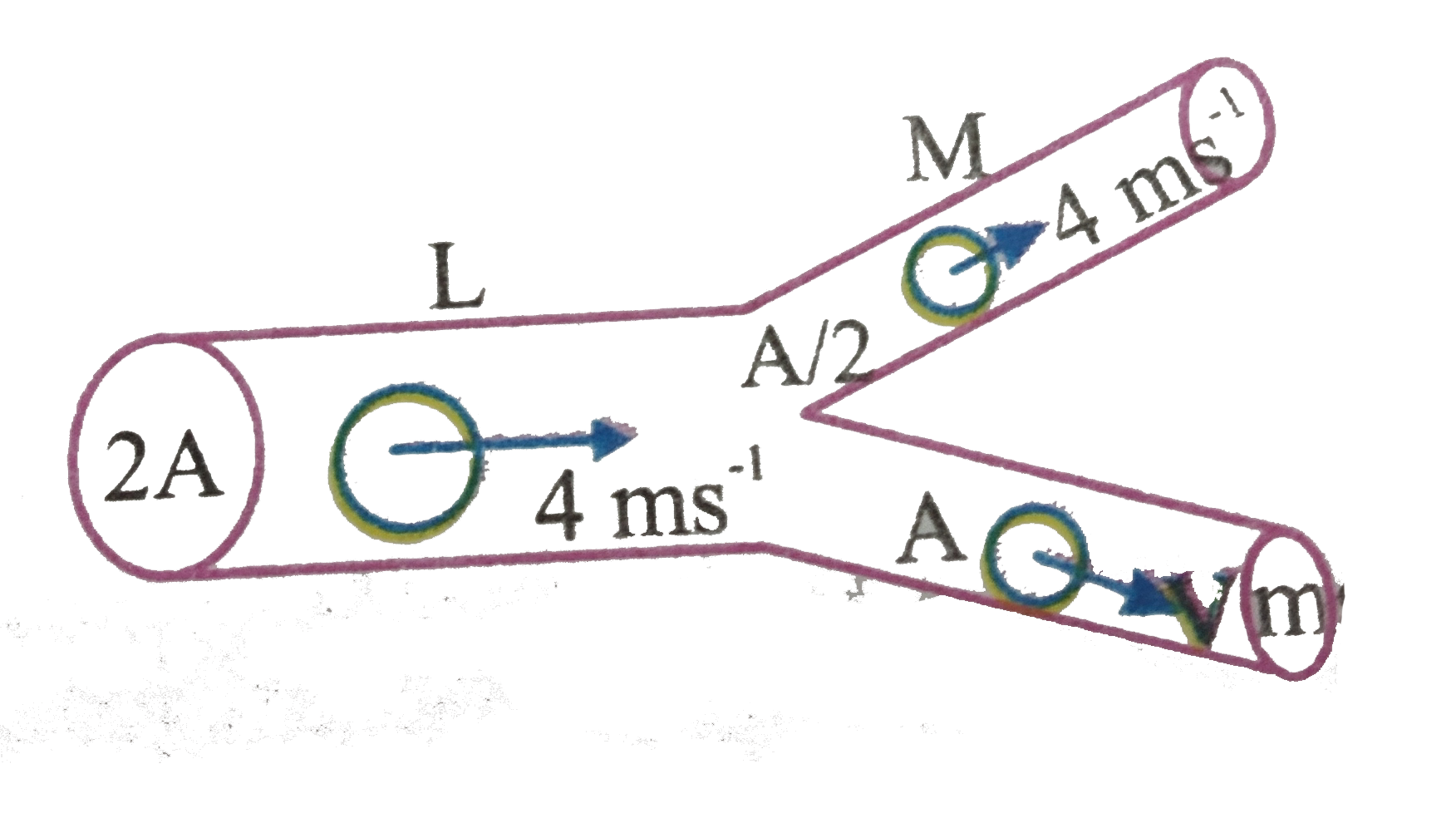
An incompressible liquid flows through a horizontal tube LMN as shown in the figure. Then the velocity V of the liquid throught he tube N is:
View SolutionA liquid of density ρ is filled in a vessel up to height H and a hole of cross section area A is made at a depth h below the free surface of liquid. The speed of liquid coming out of the hole is independent of
View SolutionAn engine pumps a liquid of density 'd' continuously through a pipe of area of cross-section A. If the speed with which the liquid passes through a pipe is v, then force exerted on liquid.
View Solution

